Nội dung bài viết

    Xem thêm

    Vở thực hành Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức

    Với giải Vở thực hành Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 Bài 5.

    1 2,120 18/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Vở thực hành Toán lớp 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức

    Câu hỏi trắc nghiệm trang 25 VTH Toán 7 Tập 1

    Câu 1 trang 25 VTH Toán 7 Tập 1: Trong bốn số 138;−13518;35147;13255, số không viết được dưới dạng số thập phân hữu hạn là

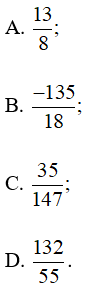
    Vở thực hành Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức (ảnh 1)

    Lời giải:

    Đáp án đúng là C

    Ta có: −13518=−152;  35147=521; 13255=125

    Ta lại có: 

    8 = 23 nên 138 viết được dưới dạng số thập phân hữu hạn.

    2 = 2 nên -152 hay −13518 viết được dưới dạng số thập phân hữu hạn.

    21 = 3.7 mà 3, 7 là các số nguyên tố khác 2 và 5 nên 521 hay 35147 viết được dưới dạng số thập phân vô hạn không tuần hoàn.

    5 = 5 nên 125 hay 13255 viết được dưới dạng số thập phân hữu hạn.

    Câu 2 trang 25 VTH Toán 7 Tập 1: Muốn làm tròn số với độ chính xác 0,0005 ta có thể làm tròn số đó đến hàng

    A. đơn vị;

    B. phần trục;

    C. phần trăm;

    D. phần nghìn.

    Lời giải:

    Đáp án đúng là D

    Độ chính xác là 0,0005 ta có thể làm tròn số đó đến hàng phần nghìn.

    Bài tập trang 25, 26 VTH Toán 7 Tập 1

    Bài 1 (2.1) trang 25 VTH Toán 7 Tập 1: Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn?

    0,1; –1,(23); 11,2(3); –6,725.

    HD: Xét các chữ số ở phần thập phân (đứng sau dấu phẩy).

    Lời giải:

    Số 0,1 có một chữ số đứng sau dấu phẩy nên 0,1 là số thập phân hữu hạn.

    Số – 6,725 có ba chữ số đứng sau dấu phẩy, nên – 6,725 là số thập phân hữu hạn.

    Số – 1,(23) viết đầy đủ là – 1,23232323..., có nhóm hai chữ số 23 được lặp lại mãi. Vì vậy số – 1,(23) là số thập phân vô hạn tuần hoàn.

    Số 11,2(3) viết đầy đủ là 11,23333333..., có chữ số 3 được lặp lại mãi. Vì vậy số 11,2(3) là số thập phân vô hạn tuần hoàn.

    Bài 2 (2.2) trang 25 VTH Toán 7 Tập 1: Sử dụng chu kì, hãy viết gọn số thập phân vô hạn tuần hoàn 0,010101…

    HD: Chu kì là nhóm chữ số sau dấu phẩy lặp đi lặp lại. Trong các viết gọn, các chữ số của chu kì được viết gọn trong dấu ngoặc đơn.

    Lời giải:

    Các chữ số ở phần thập phân của số đã cho là 0 và 1. Ta thấy nhóm hai chữ số 01 được lặp đi lặp lại mãi, vì vậy có thể viết gọn số đã cho thành 0,(01).

    Bài 3 (2.3) trang 25 VTH Toán 7 Tập 1: Tìm chữ số thập phân thứ năm của số 3,2(31) và làm tròn số 3,2(31) đến chữ số thập phân thứ năm.

    HD: Viết số thập phân đã cho dưới dạng đầy đủ.

    Lời giải:

    Viết số thập phân đã cho dưới dạng đầy đủ ta được 3,2313131... Do đó chữ số thập phân thứ năm của số đã cho là 1. Nếu làm tròn số đã cho đến chữ số thập phân thứ năm thì chữ số ngay sau hàng làm tròn là 3 < 5 nên kết quả làm tròn là 3,23131.

    Bài 4 (2.4) trang 25 VTH Toán 7 Tập 1: Số 0,1010010001000010… (viết liên tiếp các số 10, 100, 1000, 10000, … sau dấu phẩy) có phải là số thập phân vô hạn tuần hoàn hay không?

    Lời giải:

    Giả sử số đã cho là số thập phân vô hạn tuần hoàn với chu kì có n chữ số và chu kì bắt đầu từ chữ số thứ m sau dấu phẩy. Trong cách viết số thập phân đã cho, đến một lúc nào đó sẽ gặp số 100 ...0 (m + n chữ số 0). Như vậy, tới một lúc nào đó, trong phần thập phân của số đã cho có m + n chữ số 0 liên tiếp. Vì chu kì có n chữ số nên trong m + n chữ số 0 liên tiếp đó có n chữ số 0, vì thế chu kì gồm toàn chữ số 0. Do đó, đến một vị trí nào đó sau dấu phẩy, tất cả các chữ số là chữ số 0 có thể bỏ đi (mà không cần viết các chữ số 0 đó). Nhưng như vậy số đã cho lại là số thập phân hữu hạn, trái với giả thiết số đã cho là số thập phân vô hạn tuần hoàn.

    Vậy không thể xảy ra khả năng số đã cho là số thập phân vô hạn tuần hoàn.

    Do đó số đã cho là số thập phân vô hạn không tuần hoàn.

    Bài 5 (2.5) trang 26 VTH Toán 7 Tập 1: Làm tròn số 3,14159…

    a) đến chữ số thập phân thứ ba;

    b) với độ chính xác 0,005.

    Lời giải:

    a) Chữ số thập phân thứ ba của 3,14159… là 1. Chữ số đứng ngay sau nó là 5, vì vậy nếu làm tròn 3,14159… đến chữ số thập phân thứ ba thì 3,14159… ≈ 3,142.

    b) Muốn làm tròn với độ chính xác 0,005 ta phải làm tròn số đã cho đến hàng phần trăm. Chữ số hàng làm tròn là 4; chữ số đứng ngay sau hàng làm tròn là 1 (1 < 5). Vì vậy làm tròn 3,14159… với độ chính xác 0,005 ta được 3,14159… ≈ 3,14.

    Xem thêm lời giải Vở thực hành Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

    Bài 4: Thứ tự thực hiện phép tính. Quy tắc chuyển vế

    Luyện tập chung trang 19, 20, 21

    Bài ôn tập cuối chương 1

    Bài 6: Số vô tỉ. Căn bậc hai số học

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,120 18/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: