Nội dung bài viết

    Xem thêm

     Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3). Chứng minh các điểm

    Lời giải Bài 1 trang 28 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.

    1 471 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Chuyên đề Toán 11 Chân trời sáng tạo Bài 5: Phép quay

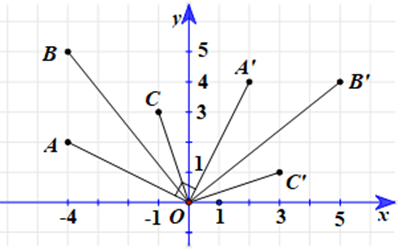
    Bài 1 trang 28 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3).

    a) Chứng minh các điểm A’(2; 4), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.

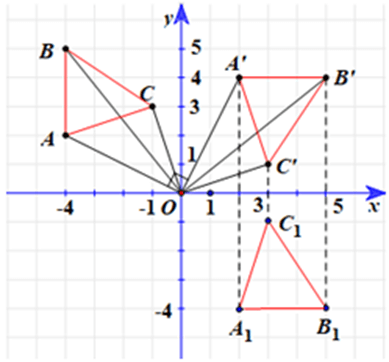
    b) Gọi ∆A1B1C1 là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của ∆A1B1C1.

    Lời giải:

    a)

    Bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo

    Với A(–4; 2) và A’(2; 4), ta có OA→=−4;2,OA'→=2;4,AA'→=6;2.

    Do đó OA=OA'=25 và AA'=210.

    Suy ra cosAOA'^=OA2+OA'2−AA'22.OA.OA'=252+252−21022.25.25=0.

    Do đó AOA'^=90°.

    Mà khi quay đoạn OA (với tâm O) theo hướng cùng chiều kim đồng hồ một góc 90° thì ta được đoạn OA’. Tức là, phép quay có góc quay lượng giác theo chiều âm một góc 90°.

    Vì vậy góc lượng giác (OA, OA’) = –90°.

    Vậy A’ là ảnh của A qua phép quay tâm O với góc quay –90°.

    Chứng minh tương tự, ta thu được B’, C’ theo thứ tự là ảnh của B, C qua phép quay tâm O với góc quay –90°.

    b) Từ câu a, ta có phép quay tâm O, góc quay –90° biến ∆ABC thành ∆A’B’C’.

    Ta có: ∆A1B1C1 là ảnh của ∆A’B’C’ qua phép đối xứng trục Ox nên:

    • A1 = ĐOx(A’), do đó hai điểm A1­ và A’(2; 4) có cùng hoành độ và có tung độ đối nhau, suy ra A1(2; –4).

    • B1 = ĐOx(B’), do đó hai điểm B1­ và B’(5; 4) có cùng hoành độ và có tung độ đối nhau, suy ra B1(5; –4).

    • C1 = ĐOx(C’), do đó hai điểm C1­ và C’(3; 1) có cùng hoành độ và có tung độ đối nhau, suy ra C1(3; –1).

    Vậy tọa độ các đỉnh của ∆A1B1C1 thỏa mãn yêu cầu bài toán là A1(2; –4), B1(5; –4), C1(3; –1).

    Bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

    Khởi động trang 25 Chuyên đề Toán 11: Vẽ mỗi hình sau ra một tờ giấy, cắt rời mỗi hình theo hình tròn. Tìm một điểm O ...

    Khám phá 1 trang 25 Chuyên đề Toán 11: a) Tìm phép biến hình biến ∆BAC thành ∆BA’C’ (Hình 1).

    Thực hành 1 trang 26 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh...

    Vận dụng 1 trang 27 Chuyên đề Toán 11: Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:

    Khám phá 2 trang 27 Chuyên đề Toán 11: Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng)...

    Thực hành 2 trang 28 Chuyên đề Toán 11: Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay Q(I, 90°) của các hình sau:...

    Vận dụng 2 trang 28 Chuyên đề Toán 11: Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay

    Bài 1 trang 28 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3).

    Bài 2 trang 29 Chuyên đề Toán 11: Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N...

    Bài 3 trang 29 Chuyên đề Toán 11: Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC,...

    Bài 4 trang 29 Chuyên đề Toán 11: Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.

    Bài 5 trang 29 Chuyên đề Toán 11: Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O...

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

    Bài 3: Phép đối xứng trục

    Bài 4: Phép đối xứng tâm

    Bài 6: Phép vị tự

    Bài 7: Phép đồng dạng

    Bài tập cuối chuyên đề 1

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 471 03/07/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: