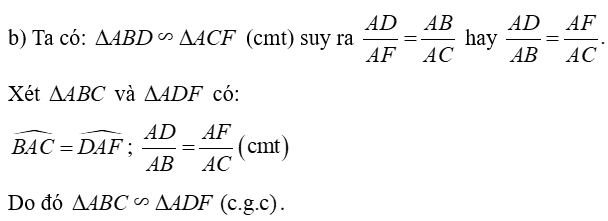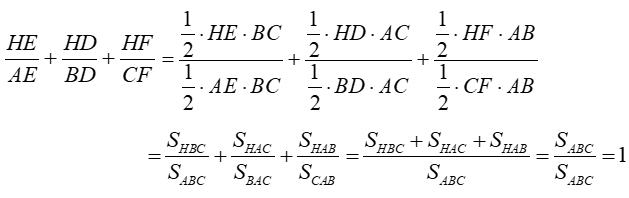TOP 10 đề thi Học kì 2 Toán 8 (Cánh diều) năm 2025 có đáp án
Bộ đề thi Học kì 2 Toán 8 (Cánh diều) năm 2025 có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 8 Học kì 2. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi Học kì 2 Toán 8 Cánh diều bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Bộ đề thi Học kì 2 Toán 8 (Cánh diều) năm 2024 có đáp án
Phòng Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Cánh diều
Năm học ...
Môn: Toán 8
Thời gian làm bài: phút
(Đề số 1)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
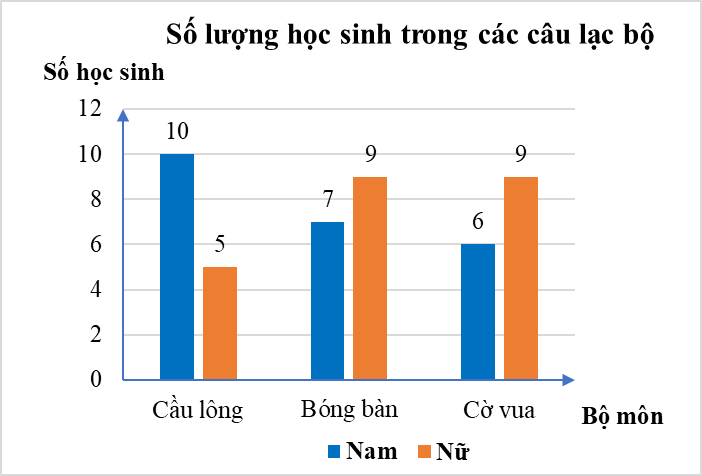
Câu 1. Mỗi câu lạc bộ tại trường Trung học Kim Đồng có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây:
Biết trong biểu đồ, dữ liệu thống kê của một câu lạc bộ chưa chính xác, đó là
A. Cầu lông.
B. Bóng bàn.
C. Cờ vua.
D. Không có dữ liệu chưa chính xác trong biểu đồ.
Câu 2. Lớp 8C có 38 bạn, trong đó có 17 nữ. Cô giáo chọn ngẫu nhiên một bạn làm sao đỏ. Xác suất cô chọn trúng một bạn nam là
A. .
B. .
C. .
D. .
Câu 3. Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 0x + 3 = 0.
B. x2 - 2 = 0.
C. .
D. .
|
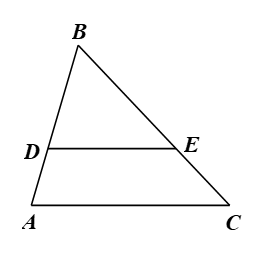
Câu 4. Cho hình vẽ bên, biết DE // AC. Tỉ số nào sau đây là đúng? A. . B. . C. . D. . |
|
Câu 5. Cho các mệnh đề sau:
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
(II) Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.
Hãy chọn đáp án đúng:
A. Cả (I) và (II) đều đúng.
B. Chỉ có (II) đúng.
C. Chỉ có (I) đúng.
D. Cả (I) và (II) đều sai.
Câu 6. Cho ∆RSK và ∆RSK có , khi đó ta có
A. ∆RSK ᔕ ∆MPQ.
B. ∆RSK ᔕ ∆PQM.
C. ∆RSK ᔕ ∆QPM.
D. ∆RSK ᔕ ∆QMP.
PHẦN II. TỰ LUẬN (7,0 điểm)
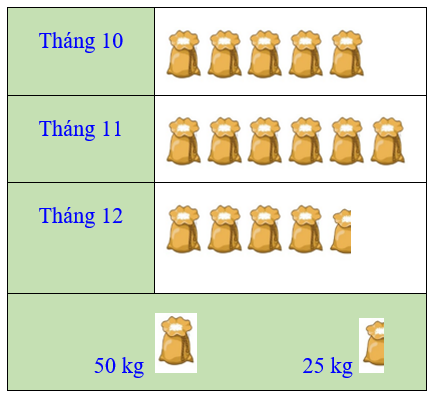
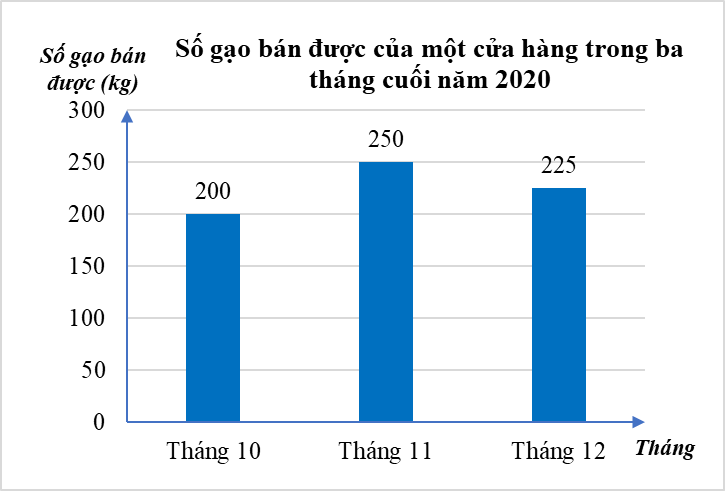
Bài 1. (1,0 điểm) Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.
a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 theo mẫu sau:
|
Năm |
Tháng 10 |
Tháng 11 |
Tháng 12 |
|
Số gạo bán được (kg) |
|
|
|
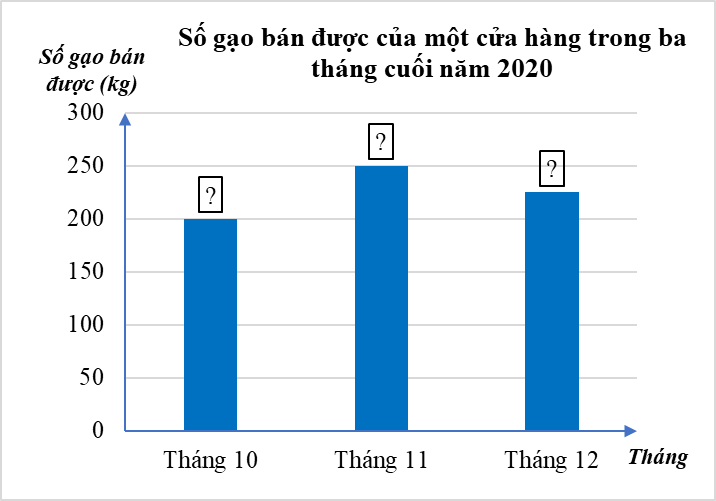
b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.
Bài 2. (1,5 điểm) Hiệu hai số là 12. Nếu chia số bé cho 7 và lớn cho 5 thì thương thứ nhất lớn hơn thương thứ hai là 4 đơn vị. Tìm hai số đó.
Bài 3. (1,0 điểm) Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, cô giáo đã chọn ra 10 học sinh gồm 4 học sinh nữ nữ là Hoa; Mai; Linh; My; 6 học sinh nam là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm 10 học sinh tập múa trên.
a) Tìm số phần tử của tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra.
Bài 4. (3,0 điểm)
1. Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm A đến trường (tại điểm B phải leo lên và xuống một con dốc với đỉnh dốc tại điểm C (như hình vẽ).
Điểm H là một điểm thuộc đoạn thẳng AB sao cho CH đường là phân giác , AH = 0,32 km và BH = 0,4 km. Biết bạn Hải đi xe đạp đến C lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?
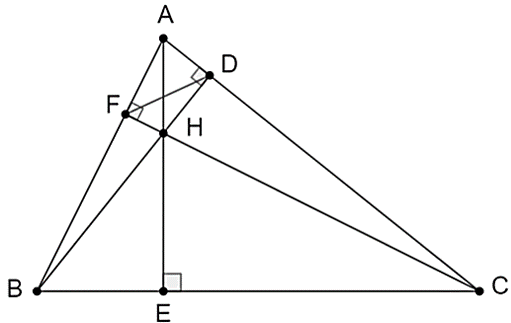
2. Cho tam giác ABC có ba góc nhọn (AB < AC) có ba đường cao AE, BD, CF cắt nhau tại H.
a) Chứng minh: ∆ABD đồng dạng với ∆ACF.
b) Chứng minh: ∆ADF đồng dạng với ∆ABC.
c) Chứng minh: BH.BD + CH.CF = BC2 và = 1.
Bài 5. (0,5 điểm) Tìm nghiệm nguyên của phương trình 2xy - x + y = 3.
−−−−−HẾT−−−−−
ĐÁP ÁN & HƯỚNG DẪN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án trắc nghiệm:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
|
Đáp án |
B |
D |
C |
B |
C |
A |
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,0 điểm)
a) Ta có bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 như sau:
|
Năm |
Tháng 10 |
Tháng 11 |
Tháng 12 |
|
Số gạo bán được (kg) |
200 |
250 |
225 |
b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là:
Bài 2. (1,5 điểm)
Gọi số bé là x ().
Số lớn là x + 12.
Chia số bé cho 7 ta được thương là .
Chia số lớn cho 5 ta được thương là .
Vì thương thứ nhất lớn hơn thương thứ hai 4 đơn vị nên ta có phương trình:
7(x + 12) - 5x = 140
7x + 84 - 5x = 140
2x = 56
x = 28
Vậy số bé là 28; số lớn là: 28 + 12 = 40.
Bài 3. (1,0 điểm)
a) Tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra là :
M = {Hoa; Mai; Linh; My; Cường; Hường; Mỹ; Kiên; Phúc; Hoàng}.
Số phần tử của tập hợp M là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn ra là học sinh nam” đó là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng.
Vì thế xác suất của biến cố đó là .
Bài 4. (3,0 điểm)
1.
Thời gian để bạn Hải đi từ A đến C là: 6 giờ 30 phút - 6 giờ = 30 phút = 0,5 giờ.
Quãng đường mà bạn Hải đi từ A đến C trong 0,5 giờ với tốc độ trung bình lên dốc 4 km/h là: AC = = 4.0,5 = 2 (km).
Xét ∆ACB có CH là đường phân giác của , nên ta có:
hay . Suy ra (km).
Thời gian để bạn Hải đi hết quãng đường2,5 km với tốc độ trung bình xuống dốc 10 km/h là: (giờ).
Như vậy, tổng thời gian bạn Hải đi từ A đến trường B là:
0,5 + 0,25 = 0,75 (giờ) = 45 (phút).
2.
Vì H là giao của ba đường cao AE, BD, CF nên H là trực tâm của tam giác ABC.
a) Xét ∆ABD và ∆ACF có:
;
Do đó .
• Mặt khác, ta có:
Bài 5. (0,5 điểm)
Ta có 2xy - x + y = 3
4xy - 2x + 2y = 6
4xy - 2x + 2y - 1 = 6 - 1
2x(2y - 1) + (2y - 1) = 6 - 1
(2y - 1)(2y - 1) = 5
Ta có x và y là các số nguyên nên 2x + 1 và 2y - 1 là các số nguyên và là ước của 5.
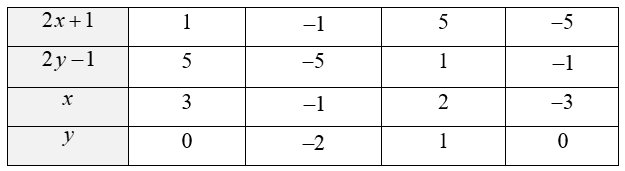
Từ đó, ta có bảng sau:
Vậy phương trình có nghiệm là: .
−−−−−HẾT−−−−−
................................
................................
................................
Xem thêm các chương trình khác:
- TOP 100 Đề thi Khoa học tự nhiên 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Giáo dục công dân 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Lịch sử và Địa lí 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tiếng Anh 8 (cả năm) (Global success) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Công nghệ 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tin học 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Toán 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Ngữ văn 8 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Khoa học tự nhiên 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Giáo dục công dân 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Lịch sử và Địa lí 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tin học 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Công nghệ 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tiếng Anh 8 (cả năm) (Friends plus) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Toán 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Ngữ văn 8 (cả năm) (Chân trời sáng tạo) năm 2024 - 2025 có đáp án