TOP 10 đề thi Học kì 1 Toán 8 (Cánh diều) năm 2023 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Học kì 1 Toán 8 Cánh diều bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Bộ đề thi Học kì 1 Toán 8 (Cánh diều) năm 2023 có đáp án

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Cánh diều

Năm học ...

Môn: Toán lớp 8

Thời gian làm bài: phút

Đề thi Học kì 1 Toán 8 Cánh diều - Đề 1

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Biểu thức nào dưới đây không phải là đơn thức?

A. \( - \frac{1}{5}.\)

B. \(5x + 9.\)

C. \({x^3}{y^2}.\)

D. \({x^2}y.\)

Câu 2. Giá trị biểu thức \(M = \frac{1}{8}{x^3} - \frac{3}{2}{x^2} + 6x - 8\) tại \(x = 24\) là

A. \(1\,\,000.\)

B. \(2\,\,700.\)

C. \(3\,\,000.\)

D. \(6\,\,400.\)

Câu 3. Giả sử các biểu thức đều có nghĩa. Với giá trị nào của \(a\) thì hai phân thức \(\frac{x}{{x + 1}}\) và \(\frac{{a{x^2} - ax}}{{{x^2} - 1}}\) bằng nhau?

A. \( - 1.\)

B. \[1.\]

C. \(2.\)

D. \(3.\)

Câu 4. Phân thức đối của phân thức \(\frac{{3x}}{{x + y}}\) là

A. \(\frac{{3x}}{{x - y}}.\)

B. \(\frac{{x + y}}{{3x}}.\)

C. \( - \frac{{3x}}{{x + y}}.\)

D. \( - \frac{{3x}}{{x - y}}.\)

Câu 5. Hàm số nào sau đây là hàm số bậc nhất?

A. \(y = 2x - 1.\)

B. \(y = 2.\)

C. \[y = {x^2} + x + 1.\]

D. \(y = \frac{2}{x}.\)

Câu 6. Đồ thị hàm số \(y = x + 2\) đi qua điểm có tọa độ nào sau đây?

A. \(\left( {0; - 2} \right).\)

B. \(\left( {1;3} \right).\)

C. \(\left( { - 1;0} \right).\)

D. \(\left( {0;0} \right).\)

Câu 7. Hệ số góc của đường thẳng \(y = \frac{{1 - 4x}}{2}\) là

A. \( - 4.\)

B. \( - 2.\)

C. \(\frac{1}{2}.\)

D. \(1.\)

Câu 8. Giá trị \(m\) để đường thẳng \(y = \left( {m - 1} \right)x + 3\) (với \(m \ne 1)\) song song với đường thẳng \(y = x\) là

A. \(m = 0.\)

B. \(m = 1.\)

C. \(m = 2.\)

D. Không có giá trị của \(m.\)

Câu 9. Tổng số cạnh bên và cạnh đáy của một hình chóp tam giác đều là

A. 4.

B. 6.

C. 8.

D. 10.

Câu 10. Diện tích xung quanh của hình chóp đều bằng

A. Tích nửa chu vi đáy và đường cao của hình chóp.

B. Tích nửa chu vi đáy và trung đoạn.

C. Tích chu vi đáy và trung đoạn.

D. Tổng chu vi đáy và trung đoạn.

Câu 11. Tứ giác \[ABCD\] có \[\widehat {C\,} = 50^\circ ,\] \(\widehat {D\,} = 60^\circ ,\) \(\widehat {A\,\,}:\widehat {B\,} = 3:2.\) Số đo \(\widehat {B\,}\) bằng

A. \(50^\circ .\)

B. \(100^\circ .\)

C. \(150^\circ .\)

D. \(200^\circ .\)

Câu 12. Phát biểu nào sau đây là sai?

A. Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là hình vuông.

B. Tứ giác có hai đường chéo bằng nhau là hình bình hành.

C. Tứ giác có 4 cạnh bằng nhau là hình thoi.

D. Tứ giác có 4 góc bằng nhau là hình chữ nhật.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm) Phân tích các đa thức sau thành nhân tử:

a) \(25{x^2}\left( {x - 3y} \right) - 15\left( {3y - x} \right);\)

b) \({x^4} - 5{x^2} + 4.\)

Bài 2. (1,5 điểm) Cho biểu thức \(A = \left( {\frac{{2x - {x^2}}}{{2{x^2} + 8}} - \frac{{2{x^2}}}{{{x^3} - 2{x^2} + 4x - 8}}} \right) \cdot \left( {\frac{2}{{{x^2}}} - \frac{{x - 1}}{x}} \right).\)

a) Tìm điều kiện xác định của biểu thức \(A.\)

b) Rút gọn biểu thức \(A.\)

c) Tính giá trị của biểu thức \(A\) khi \(x = 2\,\,024.\)

Bài 3. (1,0 điểm) Trong giờ thực hành thí nghiệm, một học sinh thả một miếng chì có khối lượng \(0,31\) kg đang ở nhiệt độ \(100^\circ {\rm{C}}\) vào \(0,25\) kg nước đang ở nhiệt độ \(58,5^\circ {\rm{C}}.\) Biết nhiệt dung riêng của nước là \(4\,\,200\) J/kg.K, nhiệt dung riêng của chì là 130 J/kg.K. gọi \(t^\circ {\rm{C}}\) là nhiệt độ khi đạt trạng thái cân bằng nhiệt, \({Q_{nuoc}}\) (J) là nhiệt lượng nước thu vào để tăng nhiệt độ từ \(58,5^\circ {\rm{C}}\) lên \(t^\circ {\rm{C,}}\) \({Q_{chi}}\) (J) là nhiệt lượng chì tỏa ra để giảm nhiệt độ từ \(100^\circ {\rm{C}}\) xuống \(t^\circ {\rm{C}}{\rm{.}}\)

a) Biết công thức tính nhiệt lượng thu vào/ tỏa ra là: \(Q = m \cdot c \cdot \Delta t\) (J), trong đó \(m\) là khối lượng của vật (kg), \(c\) là nhiệt dung riêng của chất làm nên vật (J/kg.K) và \(\Delta t = {t_2} - {t_1}\) là độ tăng/giảm nhiệt độ của vật \(\left( {^\circ {\rm{C}}} \right)\) với \({t_1}\) là nhiệt độ ban đầu, \({t_2}\) là nhiệt độ cuối cùng.

Viết công thức tính \({Q_{chi}}\) theo \(t.\) Công thức này có phải là hàm số bậc nhất không? Nếu có, hãy tìm các hệ số \(a,b\) của nó.

b) Khi có sự cân bằng nhiệt thì nhiệt độ của nước và chì là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Bài 4. (3,0 điểm)

1) Cho hình chóp tam giác đều \(S.ABC\) có các mặt bên cũng là các tam giác đều. Gọi \(SO\) là đường cao của hình chóp, \(OC = 2\sqrt 3 {\rm{\;cm}}.\)

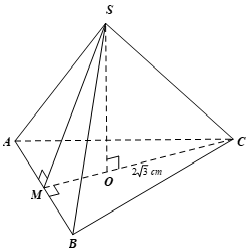
Tính (làm tròn các kết quả đến chữ số thập phân thứ hai):

a) Độ dài các cạnh bên của hình chóp.

b) Diện tích xung quanh của hình chóp.

2) Cho \(\Delta ABC\) cân tại \(A,\) đường trung tuyến \(AH.\) Gọi \(I\) và \(K\) lần lượt là trung điểm của \(AC\) và \(AB.\) Gọi \(E\) là điểm sao cho \(I\) là trung điểm của \(HE.\)

a) Giải thích tại sao tứ giác \(AKHI\) là hình thoi.

b) Chứng minh rằng \(AHCE\) là hình chữ nhật. Tam giác \(ABC\) cần thêm điều kiện gì để tứ giác \(AHCE\) là hình vuông?

Bài 5. (0,5 điểm) Cho ba số thực \(a,\,\,b,\,\,c\) khác \(2\) và thỏa mãn \(a + b + c = 6.\) Tính giá trị của biểu thức:

\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}.\)

-----HẾT-----

ĐÁP ÁN

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Bảng đáp án trắc nghiệm:

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Cánh diều

Năm học ...

Môn: Toán lớp 8

Thời gian làm bài: phút

Đề thi Học kì 1 Toán 8 Cánh diều - Đề 2

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Rút gọn biểu thức \(\left( {x + 1} \right)\left( {x - 1} \right) - \left( {x + 2} \right)\left( {x - 2} \right)\) ta được

A. \(5.\)

B. \(4.\)

C. \(3.\)

D. \( - 3.\)

Câu 2. Phân thức nào sau đây có mẫu thức là \( - 1 - {x^2}\) và tử thức là \[xy + {y^2}?\]

A. \[\frac{{ - 1 - {x^2}}}{{xy + {y^2}}}.\]

B. \[ - \frac{{1 - {x^2}}}{{xy + {y^2}}}.\]

C. \[ - \frac{{xy + {y^2}}}{{1 - {x^2}}}.\]

D. \[\frac{{xy + {y^2}}}{{ - 1 - {x^2}}}.\]

Câu 3. Cho hàm số được xác định bởi công thức \(y = ax + 3.\) Biết đồ thị hàm số này đi qua điểm \[\left( {1;5} \right).\] Tung độ của điểm thuộc đồ thị hàm số có hoành độ bằng \( - 5\) là

A. \( - 7.\)

B. \(1.\)

C. \( - 4.\)

D. \( - 20.\)

Câu 4. Cho hai đường thẳng \(d:y = ax + b\,\,\left( {a \ne 0} \right)\) và \[d':y = a'x + b'\,\,\left( {a' \ne 0} \right).\] Với điều kiện nào sau đây thì hai đường thẳng \(d\) và \(d'\) cắt nhau?

A. \(a = a'.\)

B. \(a = a'\) và \(b = b'.\)

C. \(a \ne a'.\)

D. \(a = a'\) và \[b \ne b'.\]

Câu 5. Chân đường cao của hình chóp tam giác đều là

A. Trọng tâm của tam giác.

B. Trực tâm của tam giác.

C. Giao điểm của ba đường phân giác.

D. Cả A, B, C đều đúng.

Câu 6. Một hình chóp đều và một hình lăng trụ đứng có diện tích đáy bằng nhau. Chiều cao của hình chóp đều gấp đôi chiều cao của hình lăng trụ đứng. Thể tích của hình chóp đều là

A. \(V = \frac{1}{3}Sh.\)

B. \[V = Sh.\]

C. \(V = \frac{2}{3}Sh.\)

D. \(V = 2Sh.\)

Câu 7. Cho tứ giác \(MNPQ\) có \(PM\) là tia phân giác của góc \(\widehat {NPQ}.\) Biết \(\widehat {QMN} = 110^\circ ,\) \(\widehat {N\,} = 120^\circ \) và \(\widehat {Q\,} = 60^\circ .\) Số đo của \(\widehat {MPQ}\) là

A. \(25^\circ .\)

B. \(35^\circ .\)

C. \(50^\circ .\)

D. \(70^\circ .\)

Câu 8. Để chứng minh tứ giác \[ABCD\] là hình vuông, dấu hiệu nào sau đây là sai?

A. Tứ giác \[ABCD\] là hình thoi có hai đường chéo bằng nhau.

B. Tứ giác \[ABCD\] là hình thoi có một góc vuông.

C. Tứ giác \[ABCD\] là hình thoi có hai đường chéo vuông góc.

D. Tứ giác \[ABCD\] là hình chữ nhật có hai cạnh kề bằng nhau.

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Tìm \(x,\) biết:

a) \({\left( {x - 2} \right)^2} - \left( {x - 3} \right)\left( {x + 3} \right) = 6.\)

b) \(2x\left( {x - 3} \right) - 5\left( {3 - x} \right) = 0.\)

c) \(2{x^2} - x - 6 = 0.\)

Bài 2. (1,5 điểm) Cho biểu thức \[A = \frac{{{x^3} - 1}}{{{x^2} - 4}} \cdot \left( {\frac{1}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}} \right).\]

a) Viết điều kiện xác định của biểu thức \(A.\)

b) Rút gọn biểu thức \(A.\)

c) Tính giá trị của biểu thức \(A\) biết \(\left| {x + 3} \right| = 1.\)

Bài 3. (1,5 điểm) Giá trị sổ sách là giá trị của tài sản mà một công ty sử dụng để tạo ra bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm đi một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt vào tài sản. Giả sử rằng một công ty vận tải vừa mua một số ô tô mới với giá là 640 triệu đồng một chiếc. Công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá \[640:8 = 80\] (triệu đồng).

a) Tìm hàm số bậc nhất biểu thị giá trị sổ sách \[V\] (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi \[x\] (năm) của nó.

b) Vẽ đồ thị của hàm số bậc nhất tìm được ở câu a.

c) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng?

Bài 4. (3,0 điểm)

1) Bạn Hoa dự định làm 4 hộp quà có dạng hình chóp tứ giác đều như hình bên có cạnh đáy \(6{\rm{\;cm,}}\) chiều cao của mặt bên xuất phát từ đỉnh là \(4{\rm{\;cm}}.\) Tính diện tích giấy mà bạn Hoa cần dùng để làm 4 hộp quà đó.

2) Cho tam giác \[ABC\] vuông cân tại \[A.\] Lấy điểm \[M\] thuộc cạnh huyền \[BC.\] Gọi \[D,{\rm{ }}E\] lần lượt là hình chiếu của điểm \[M\] trên đường thẳng \[AB,{\rm{ }}AC.\]

a) Tứ giác \[ADME\] là hình gì? Vì sao?

b) Chứng minh khi điểm \[M\] thay đổi vị trí trên cạnh \[BC\] thì chu vi của tứ giác \[ADME\] không đổi.

c) Điểm \[M\] ở vị trí nào trên cạnh \[BC\] thì \[DE\] có độ dài nhỏ nhất? Tính độ dài nhỏ nhất đó, biết \[AB = 2{\rm{\;cm}}.\]

Bài 5. (0,5 điểm) Cho \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{1}{{x + y + z}}.\) Chứng minh rằng:

\[\frac{1}{{{x^{2023}}}} + \frac{1}{{{y^{2023}}}} + \frac{1}{{{z^{2023}}}} = \frac{1}{{{x^{2023}} + {y^{2023}} + {z^{2023}}}}.\]

-----HẾT-----

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Bảng đáp án trắc nghiệm:

.....................................

.....................................

.....................................

Xem thử tài liệu tại đây: Link tài liệu