Dạng 3: Xác định hệ số a, b, c khi biết các tính chất của hàm số bậc hai có đáp án
-
1324 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
18/07/2024
Xem đáp án
Hướng dẫn giải:
Xét hàm số y = ax2 – 4x + c có b = – 4.
Đồ thị hàm số là parabol có bề lõm hướng xuống nên ta có: a < 0
Đồ thị có đỉnh S(–2; 7) nên ta có: \(\frac{{ - b}}{{2a}} = - 2 \Leftrightarrow \frac{{ - ( - 4)}}{{2a}} = - 2 \Leftrightarrow - 4a = 4 \Leftrightarrow a = - 1\) (thỏa mãn điều kiện).
Đồ thị cắt trục tung tại điểm (0; 3) nên ta có: c = 3
Vậy hàm số y = ax2 – 4x + c có a = –1; b = –4; c = 3.
Câu 2:
22/07/2024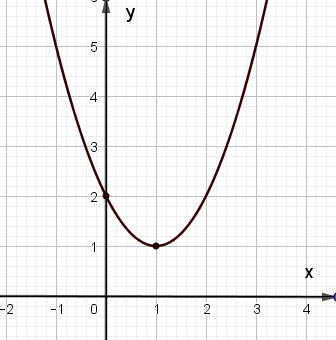
Xem đáp án
Hướng dẫn giải:
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng lên, đỉnh S(1; 1) và cắt trục tung tại điểm (0; 2).
Do đó ta có:
a > 0 (1)
\( - \frac{b}{{2a}} = 1\) (2); \( - \frac{\Delta }{{4a}} = 1 \Leftrightarrow - \frac{{{b^2} - 4ac}}{{4a}} = 1\) (3)
c = 2 (4)
Thay (4) vào (3) ta có: \( - \frac{{{b^2} - 4a.2}}{{4a}} = 1 \Leftrightarrow - {b^2} + 8a = 4a \Leftrightarrow - {b^2} + 4a = 0\) (5)
Từ (2) ta có: b = –2a (6)
Thay (6) vào (5) ta có: –(–2a)2 + 4a = 0 ⇔ –4a2 + 4a = 0
⇔ 4a(–a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = 1\,\,(TM)\end{array} \right.\)
Với a = 1 ta có: b = –2.1 = –2
Vậy hàm số y = ax2 + bx + c có a = 1, b = –2, c = 2.
Câu 3:
18/07/2024Cho đồ thị hàm số y = ax2 + bx + c trong hình vẽ sau:
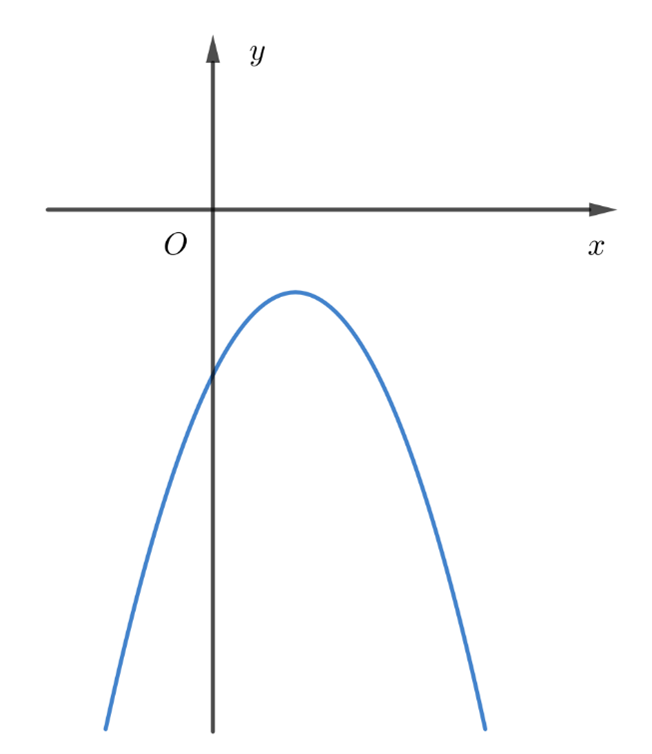
Khẳng định nào sau đây là đúng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta thấy đồ thị hàm số có bề lõm hướng xuống, do đó a < 0.
Câu 4:
17/07/2024Cho đồ thị hàm số y = ax2 trong hình vẽ sau:
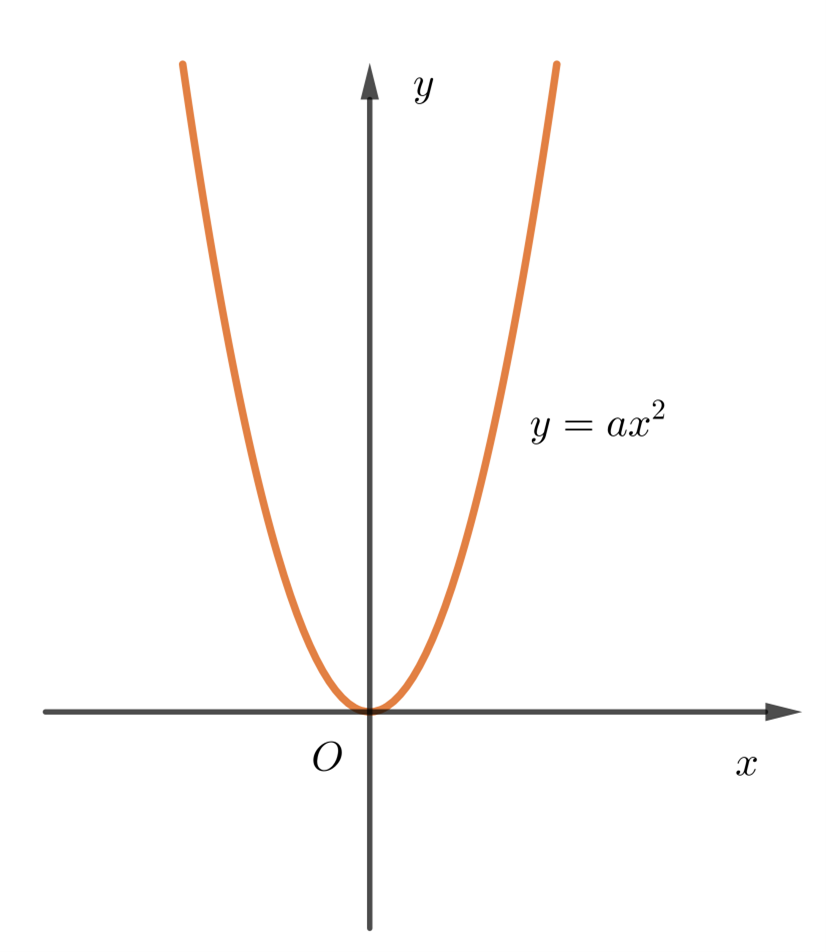
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta thấy đồ thị hàm số cắt trục tung tại điểm (0; 0) do đó c = 0.
Đồ thị có bề lõm hướng lên trên nên a > 0.
Câu 5:
23/07/2024Cho đồ thị hàm số y = ax2 + bx + c trong hình vẽ sau:
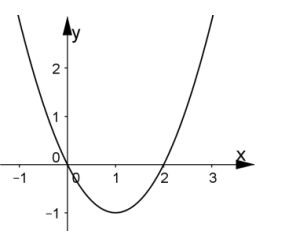
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Dựa vào đồ thị ta thấy
+ Đồ thị có bề lõm hướng lên trên nên a > 0.
+ Parabol cắt trục tung tại điểm (0; 0) nên c = 0.
+ Đỉnh của parabol có hoành độ là 1, lớn hơn 0 hay \( - \frac{b}{{2a}}\)> 0 và tung độ là – 1, nhỏ hơn 0 hay \( - \frac{\Delta }{{4a}}\)< 0.
Câu 6:
17/07/2024Cho parabol (P): y = ax2 + bx + c có trục đối xứng là đường thẳng x = 1.
Khi đó 4a + 2b bằng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Do parabol (P): y = ax2 + bx + c có trục đối xứng là đường thẳng x = 1 nên \( - \frac{b}{{2a}} = 1\)
⇔ 2a = – b ⇔ 2a + b = 0 ⇔ 2(2a + b) = 0 ⇔ 4a + 2b = 0.
Câu 7:
17/07/2024Xác định các hệ số a, b, c biết parabol có đồ thị hàm số y = ax2 + bx + c đi qua các điểm A(0; – 1), B(1; – 1), C(– 1; 1).
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Vì A ∈ (P), B ∈ (P), C ∈ (P) nên ta có hệ phương trình \(\left\{ \begin{array}{l}c = - 1\\a + b + c = - 1\\a - b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\\c = - 1\end{array} \right.\).
Vậy a = 1; b = – 1; c = – 1.
Câu 8:
22/07/2024Cho parabol y = ax2 + bx + 4 có trục đối xứng là đường thẳng x = \(\frac{1}{3}\) và đi qua điểm A(1; 3). Tổng giá trị a + 2b là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Vì parabol y = ax2 + bx + 4 có trục đối xứng là đường thẳng x = \(\frac{1}{3}\) nên \( - \frac{b}{{2a}} = \frac{1}{3}\)
⇔ 2a = – 3b ⇔ 2a + 3b = 0 (1).
Parabol đi qua điểm A(1; 3) nên a + b + 4 = 3 ⇔ a + b = – 1 ⇔ a = – 1 – b (2).
Thay (2) vào (1) ta được: 2(– 1 – b) + 3b = 0 ⇔ b = 2.
Do đó, a = – 1 – 2 = – 3.
Vậy a + 2b = – 3 + 2 . 2 = 1.
Câu 9:
17/07/2024Cho đồ thị hàm số y = ax2 + bx + c trong hình vẽ sau:
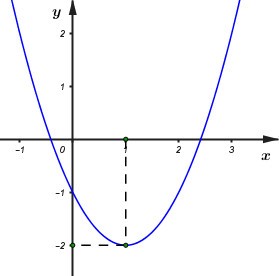Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Dựa vào đồ thị ta thấy parabol cắt trục tung tại điểm (0; –1) do đó c = –1.
Parabol có bề lõm hướng lên trên nên a > 0.
Tọa độ đỉnh của parabol là (1; – 2) nên \( - \frac{b}{{2a}}\) = 1 và \( - \frac{\Delta }{{4a}} = - 2 \Leftrightarrow \frac{\Delta }{{4a}} = 2\).
Câu 10:
17/07/2024Cho parabol (P): y = ax2 + bx + 2. Xác định hệ số a, b biết (P) có đỉnh I(2; – 2).
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Điều kiện: a ≠ 0.
(P) có đỉnh I(2; – 2) nên ta có hệ \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\ - 2 = a{.2^2} + b.2 + 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 4\end{array} \right.\).
Vậy a = 1; b = – 4.
Câu 11:
22/07/2024Cho đồ thị hàm số y = ax2 + bx + c trong hình vẽ sau:
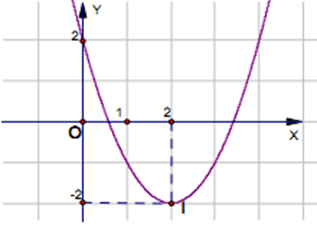
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng lên, đỉnh I(2; –2) và cắt trục tung tại điểm (0; 2).
Do đó ta có:
a > 0 (1)
\( - \frac{b}{{2a}} = 2\) (2); \( - \frac{\Delta }{{4a}} = 1 \Leftrightarrow - \frac{{{b^2} - 4ac}}{{4a}} = - 2\) (3)
c = 2 (4)
Thay (4) vào (3) ta có: \( - \frac{{{b^2} - 4a.2}}{{4a}} = - 2 \Leftrightarrow - {b^2} + 8a = - 8a \Leftrightarrow - {b^2} + 16a = 0\) (5)
Từ (2) ta có: b = –4a (6)
Thay (6) vào (5) ta có: –(–4a)2 + 16a = 0 ⇔ –16a2 + 16a = 0
⇔ 16a(–a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = 1\,\,(TM)\end{array} \right.\)
Vậy a = 1.
Câu 12:
17/07/2024Cho đồ thị hàm số y = ax2 + bx + c trong hình vẽ sau:
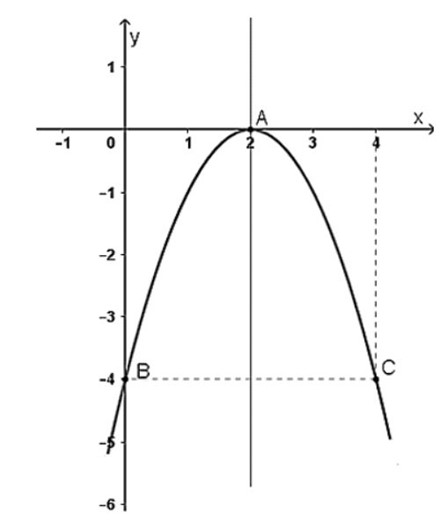
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng xuống, đỉnh I(2; 0) và cắt trục tung tại điểm (0; –4).
Do đó ta có:
a < 0 (1)
\( - \frac{b}{{2a}} = 2\) (2); \( - \frac{\Delta }{{4a}} = 1 \Leftrightarrow - \frac{{{b^2} - 4ac}}{{4a}} = 0 \Leftrightarrow {b^2} - 4ac = 0\) (3)
c = –4 (4)
Thay (4) vào (3) ta có: \({b^2} - 4a.( - 4) = 0 \Leftrightarrow {b^2} + 16a = 0\) (5)
Từ (2) ta có: b = –4a (6)
Thay (6) vào (5) ta có: (–4a)2 + 16a = 0 ⇔ 16a2 + 16a = 0
⇔ 16a(a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = - 1\,\,(TM)\end{array} \right.\)
Với a = –1 ta có: b = –4.(–1) = 4
Vậy hàm số y = ax2 + bx + c có a = –1; b = 4; c = –4