Trắc nghiệm Toán 10 CTST Bài 2. Định lí côsin và định lí sin có đáp án (Phần 2)
Trắc nghiệm Toán 10 CTST Bài 2. Định lí côsin và định lí sin có đáp án (Vận dụng)
-
594 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Cho ∆ABC. Nếu tăng cạnh AB lên 4 lần và tăng cạnh AC lên 5 lần và giữ nguyên độ lớn của \(\widehat A\) thì khi đó diện tích của tam giác mới S’ được tạo nên bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Diện tích ∆ABC ban đầu là: \(S = \frac{1}{2}.AB.AC.\sin A\).
Khi tăng cạnh AB lên 4 lần và tăng cạnh AC lên 5 lần và giữ nguyên độ lớn của \(\widehat A\) thì diện tích ∆ABC lúc này là:
\(S' = \frac{1}{2}.\left( {4AB} \right).\left( {5AC} \right).\sin A = 4.5.\frac{1}{2}AB.AC.\sin A = 20S\).
Vậy ta chọn phương án D.
Câu 2:
17/07/2024∆ABC vuông cân tại A và nội tiếp đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp ∆ABC. Khi đó tỉ số \(\frac{R}{r}\) bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Giả sử AB = AC = a.
∆ABC vuông cân tại A nên BC2 = AB2 + AC2 (Định lí Pythagore)
Do đó BC2 = a2 + a2 = 2a2.
Suy ra \(BC = a\sqrt 2 \).
Diện tích ∆ABC là: \(S = \frac{1}{2}.AB.AC = \frac{{{a^2}}}{2}\) (đơn vị diện tích)
Ta có \(S = \frac{{AB.AC.BC}}{{4R}}\)
\( \Leftrightarrow R = \frac{{AB.AC.BC}}{{4S}} = \frac{{a.a.a\sqrt 2 }}{{4.\frac{{{a^2}}}{2}}} = \frac{{a\sqrt 2 }}{2}\).
Nửa chu vi của ∆ABC là:
\(p = \frac{{AB + AC + BC}}{2} = \frac{{a + a + a\sqrt 2 }}{2} = \frac{{a\left( {2 + \sqrt 2 } \right)}}{2}\).
Ta có S = p.r
\( \Leftrightarrow r = \frac{S}{p} = \frac{{{a^2}}}{2}:\frac{{a\left( {2 + \sqrt 2 } \right)}}{2} = \frac{{{a^2}}}{2}.\frac{2}{{a\left( {2 + \sqrt 2 } \right)}} = \frac{a}{{2 + \sqrt 2 }}\).
Vì vậy tỉ số \(\frac{R}{r} = \frac{{a\sqrt 2 }}{2}:\frac{a}{{2 + \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}.\frac{{2 + \sqrt 2 }}{a} = 1 + \sqrt 2 \).
Vậy ta chọn phương án A.
Câu 3:
21/07/2024∆ABC có \(AB = \frac{{\sqrt 6 - \sqrt 2 }}{2}\), \(BC = \sqrt 3 \), \(CA = \sqrt 2 \). Gọi D là chân đường phân giác trong của \(\widehat A\). Khi đó số đo của \(\widehat {ADB}\) bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
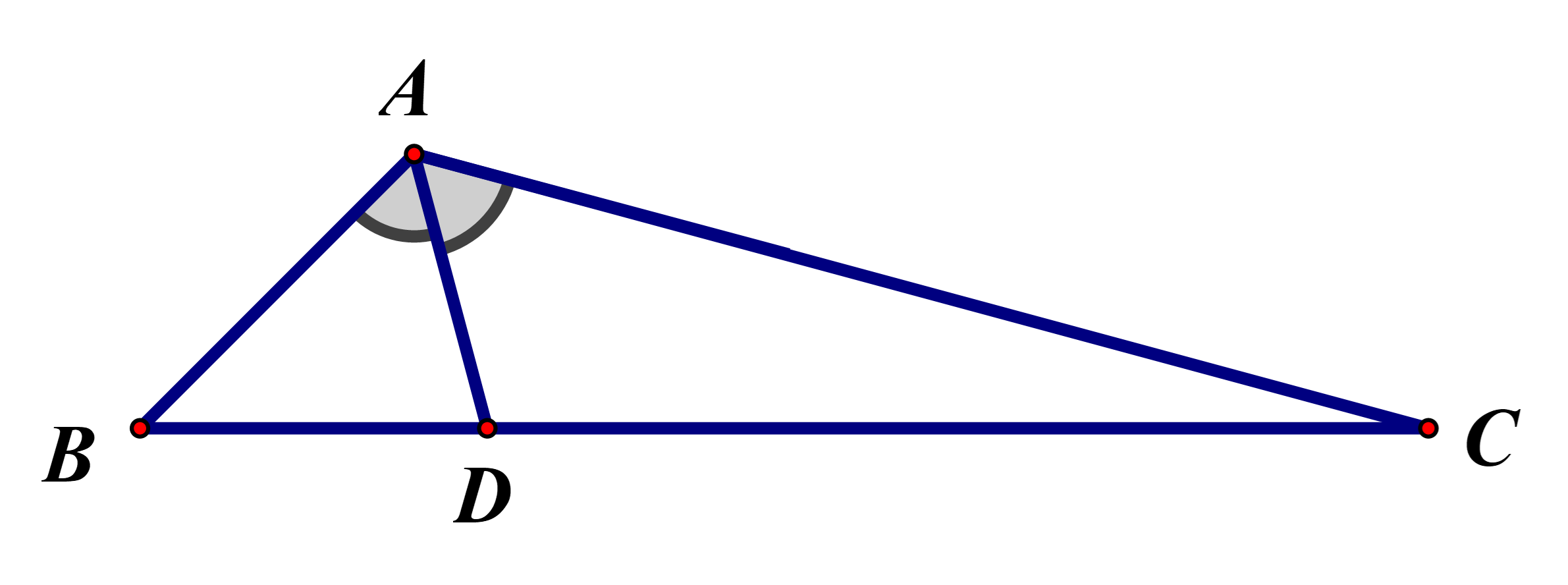
Áp dụng hệ quả của định lí côsin cho ∆ABC, ta có:
⦁ \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{2 - \sqrt 3 + 2 - 3}}{{2.\frac{{\sqrt 6 - \sqrt 2 }}{2}.\sqrt 2 }} = - \frac{1}{2}\).
Suy ra \(\widehat {BAC} = 120^\circ \).
⦁ \(\cos \widehat {ABC} = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{2 - \sqrt 3 + 3 - 2}}{{2.\frac{{\sqrt 6 - \sqrt 2 }}{2}.\sqrt 3 }} = \frac{{\sqrt 2 }}{2}\).
Suy ra \(\widehat {ABC} = 45^\circ \) hay \(\widehat {ABD} = 45^\circ \).
Ta có AD là tia phân giác của \(\widehat {BAC}\).
Suy ra \(\widehat {BAD} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.120^\circ = 60^\circ \).
∆ABD có: \(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \) (định lí tổng ba góc của một tam giác)
\( \Leftrightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {60^\circ + 45^\circ } \right) = 75^\circ \).
Vậy \(\widehat {ADB} = 75^\circ \).
Do đó ta chọn phương án C.
Câu 4:
21/07/2024Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
⦁ Ta xét khẳng định (I):
Áp dụng định lí côsin cho ∆ABC ta có:
b2 – c2 = c2 + a2 – 2ca.cosB – (a2 + b2 – 2ab.cosC)
= c2 + a2 – 2ca.cosB – a2 – b2 + 2ab.cosC
= c2 – b2 + 2a(b.cosC – c.cosB)
Þ b2 – c2 = c2 – b2 + 2a(b.cosC – c.cosB)
Þ 2(b2 – c2) = 2a(b.cosC – c.cosB)
Þ b2 – c2 = a(b.cosC – c.cosB).
Do đó khẳng định (I) đúng.
⦁ Ta xét khẳng định (II):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
(b + c)sinA = \[\left( {2R.\sin B + 2R.\sin C} \right).\frac{a}{{2R}}\]
\[ = \left( {\sin B + \sin C} \right).\frac{{2R.a}}{{2R}}\]
= a(sinB + sinC).
Vì vậy khẳng định (II) đúng.
⦁ Ta xét khẳng định (III):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
2R.sinB.sinC = \(2R.\frac{b}{{2R}}.\frac{c}{{2R}}\)
\( = \frac{{bc}}{{2R}} = \frac{{abc}}{{4R}}.\frac{2}{a}\)
\( = \frac{{2S}}{a} = {h_a}\).
Vì vậy khẳng định (III) đúng.
⦁ Ta xét khẳng định (IV):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
R.r.(sinA + sinB + sin C) = \(R.r.\left( {\frac{a}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right)\)
\[ = R.r.\frac{1}{R}\left( {\frac{a}{2} + \frac{b}{2} + \frac{c}{2}} \right)\]
\[ = r.\frac{{a + b + c}}{2} = r.p = S\].
Vì vậy khẳng định (IV) đúng.
Vậy có 4 khẳng định đúng, ta chọn phương án D.
Câu 5:
15/07/2024Hai tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 120°. Tàu 1 chạy với vận tốc 30 hải lí/giờ. Tàu 2 chạy với vận tốc 25 hải lí/giờ. Sau hai giờ, hai tàu cách nhau khoảng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
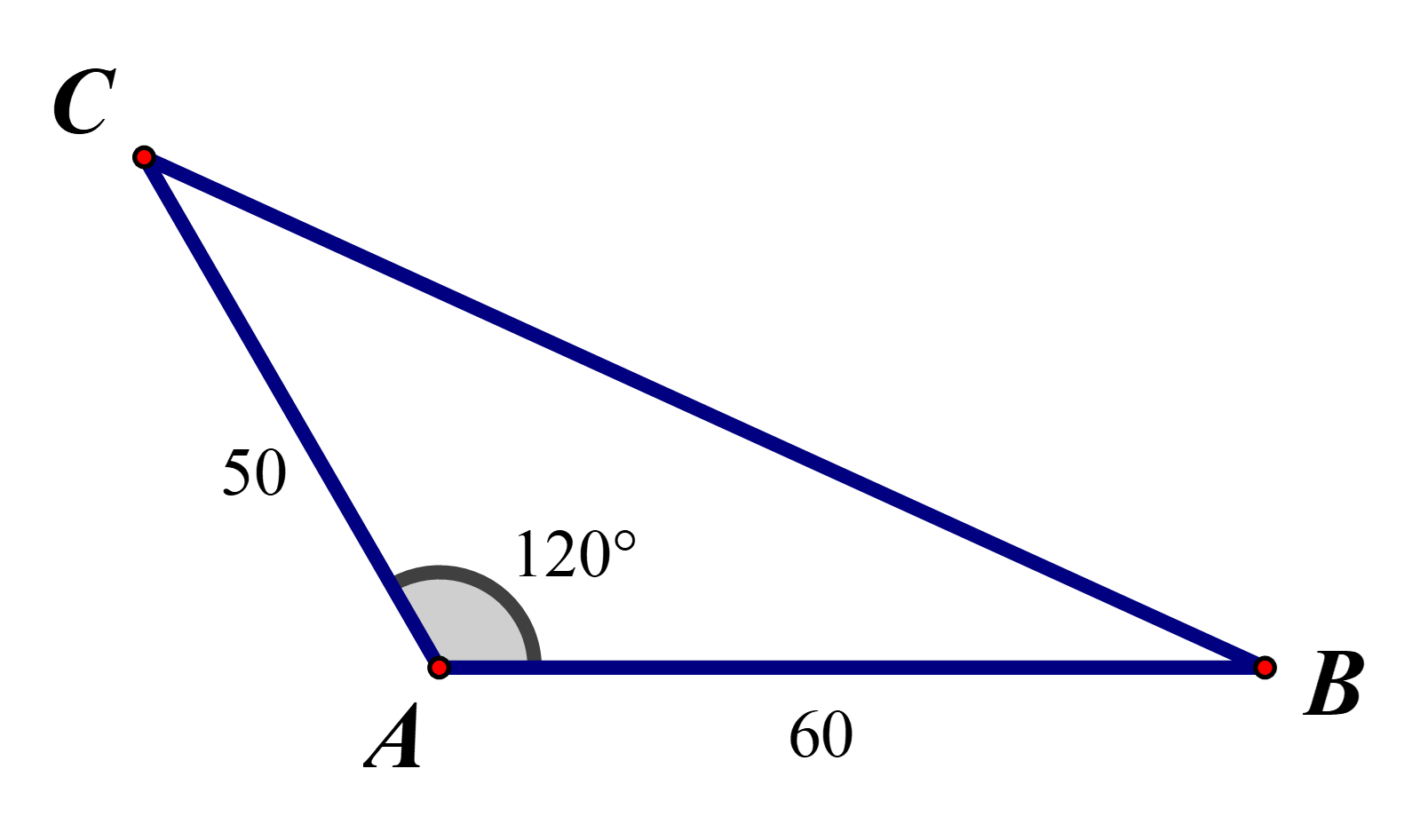
Giả sử sau hai giờ, tàu 1 đến vị trí điểm B, tàu 2 đến vị trí điểm C.
Sau hai giờ, tàu 1 đi được 2.30 = 60 (hải lí).
Suy ra AB = 60.
Sau hai giờ, tàu hai đi được 2.25 = 50 (hải lí).
Suy ra AC = 50.
Ta có BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 602 + 502 – 2.60.50.cos120°
= 9100
Suy ra BC = \(\sqrt {9100} = 10\sqrt {91} \approx 95,4\).
Vì vậy sau hai giờ, hai tàu cách nhau khoảng 95,4 hải lí.
Vậy ta chọn phương án B.