Trắc nghiệm Sự xác định đường tròn. Tính chất đối xứng của đường tròn (có đáp án)
Trắc nghiệm Toán 9 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
-
441 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Tâm đối xứng của đường tròn là:
Xem đáp án
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Đáp án cần chọn là: D
Câu 2:
20/07/2024Giao ba đường trung trực của tam giác là:
Xem đáp án
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Đáp án cần chọn là: A
Câu 3:
10/07/2024Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
Xem đáp án
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Đáp án cần chọn là: D
Câu 4:
22/07/2024Tâm đường tròn ngoại tiếp tam giác là:
Xem đáp án
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Đáp án cần chọn là: B
Câu 5:
19/07/2024Điền từ thích hợp vào chỗ trống: “Đường tròn có … trục đối xứng”
Xem đáp án
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Đáp án cần chọn là: C
Câu 6:
09/07/2024Số tâm đối xứng của đường tròn là
Xem đáp án
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Đáp án cần chọn là: A
Câu 7:
23/07/2024Cho tam giác ABC vuông tại A, có AB = 5cm; AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Xem đáp án
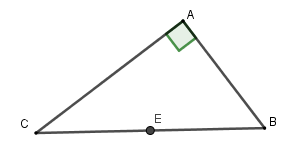
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC,
bán kính R =
Theo định lý Pytago ta có
BC = = 13
nên bán kính R =
Đáp án cần chọn là: C
Câu 8:
23/07/2024Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM = R. Chọn khẳng định đúng?
Xem đáp án
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
|
Vị trí tương đối |
Hệ thức |
|
M nằm trên đường tròn (O) |
OM = R |
|
M nằm trong đường tròn (O) |
OM < R |
|
M nằm ngoài đường tròn (O) |
OM > R |
Đáp án cần chọn là: B
Câu 9:
15/07/2024Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a.
Xem đáp án
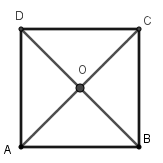
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA =
Xét tam giác ABC vuông cân tại B ta có
AC2 = AB2 + BC2
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Đáp án cần chọn là: C
Câu 10:
15/07/2024Tâm của đường tròn ngoại tiếp tam giác vuông là:
Xem đáp án
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Đáp án cần chọn là: A
Câu 11:
23/07/2024Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông?
Xem đáp án
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền
Đáp án cần chọn là: C
Câu 12:
18/07/2024Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−3; −4) và đường tròn tâm là gốc tọa độ O, bán kính R = 3
Xem đáp án
Ta có:
OA == 5 > 3 = R
nên A nằm bên ngoài đường tròn tâm O bán kính R = 3 cm
Đáp án cần chọn là: A
Câu 13:
08/07/2024Tính bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3cm
Xem đáp án
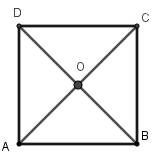
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA =
Xét tam giác ABC vuông cân tại B
ta có AC2 = AB2 + BC2 = 32 + 32 = 18
Đáp án cần chọn là: B
Câu 14:
10/07/2024Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Xem đáp án
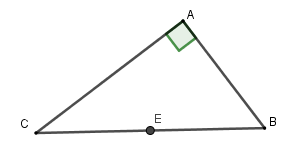
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính R =
Theo định lý Pytago ta có
BC = = 25
nên bán kính R =
Đáp án cần chọn là: B
Câu 15:
23/07/2024Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
Xem đáp án
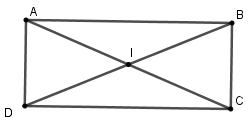
Gọi I là giao hai đường chéo,
ta có IA = IB = IC = ID
(vì BD = AC và I là trung điểm mỗi đường)
Nếu bốn điểm A, B, C, D
cùng thuộc đường tròn tâm I
bán kính R =
Theo định lý Pytago trong tam giác vuông ABC
ta có AC == 13
nên R == 6,5cm
Vậy bán kính cần tìm là R = 6,5cm
Đáp án cần chọn là: D
Câu 16:
21/07/2024Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
Xem đáp án
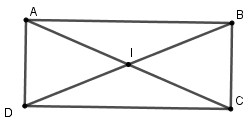
Gọi I là giao hai đường chéo,
ta có IA = IB = IC = ID
(vì BD = AC và I là trung điểm mỗi đường)
Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I
bán kính R =
Theo định lý Pytago trong tam giác vuông ABC ta có
AC = =13
nên R=
Vậy bán kính cần tìm là R = 5cm
Đáp án cần chọn là: A
