Thi Online Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án
Dạng 5: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại hoặc tính giá trị của biểu thức có đáp án
-
1076 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
30/11/2024
Xem đáp án
* Lời giải:
Vì 90° < α < 180° nên cosα < 0.
Ta có: sin2α + cos2α = 1
Suy ra cosα = \( - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - \frac{1}{9}} = - \frac{{2\sqrt 2 }}{3}\).
Do đó \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{1}{3}}}{{ - \frac{{2\sqrt 2 }}{3}}} = - \frac{1}{{2\sqrt 2 }}\)
và \(\cot \alpha = \frac{1}{{\tan \alpha }} = - 2\sqrt 2 \).
* Phương pháp giải:
Áp dụng các công thức lượng giác cơ bản để biến đổi và thực hiện phép tính
* Lý thuyết cần nắm thêm về giá trị lượng giác:
1. Giá trị lượng giác
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
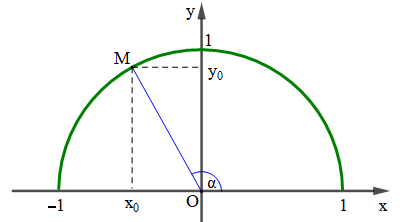
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho . Gọi (; ) là toạ độ điểm M, ta có:
- Tung độ của M là sin của góc α, kí hiệu là sinα = ;
- Hoành độ của M là côsin của góc α, kí hiệu là cosα = ;
- Tỉ số ( ≠ 0) là tang của góc α, kí hiệu là
- Tỉ số ( ≠ 0) là côtang của góc α, kí hiệu là
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.
2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
3. Giá trị lượng giác của một số góc đặc biệt
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt:
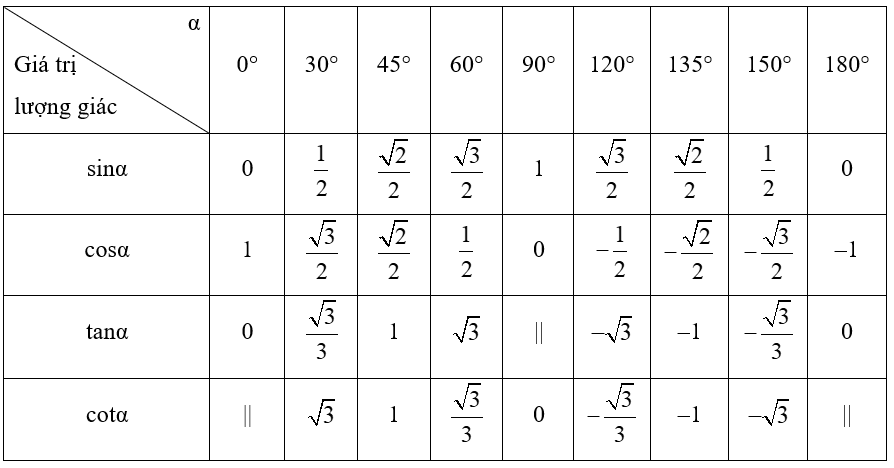Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Ví dụ 4. Tính giá trị các biểu thức sau:
a) A = .sin90° + .cos90° + .cos180°;
b) B = 3 – 135° + 2120° ‒ 3150°.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo
Giải Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Câu 2:
22/07/2024 Xem đáp án
Hướng dẫn giải:
Ta có: A = 2sin2α + 5cos2α = 2 . (1 – cos2α) + 5cos2α = 2 + 3cos2α
Với \(\cos \alpha = \frac{{\sqrt 2 }}{2}\), thay vào biểu thức A ta được
A = 2 + 3 . \({\left( {\frac{{\sqrt 2 }}{2}} \right)^2}\) = 2 + 3 . \(\frac{1}{2}\) = \(\frac{7}{2}\).
Vậy A = \(\frac{7}{2}\).
Câu 3:
19/07/2024Cho góc α (0° < α < 180°) với \(\cos \alpha = \frac{1}{3}\). Giá trị của sinα bằng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Vì 0° < α < 180° nên sinα > 0.
Lại có sin2α + cos2α = 1
Suy ra \(\sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = \frac{{2\sqrt 2 }}{3}\).
Câu 4:
23/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Vì 90° < α < 180° nên cosα < 0.
Do đó \[cos\alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - {{\left( {\frac{{12}}{{13}}} \right)}^2}} = - \sqrt {\frac{{25}}{{169}}} = - \frac{5}{{13}}\].
Câu 5:
23/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có \({\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\)
\( \Rightarrow {\cos ^2}\alpha = \frac{1}{{{{\tan }^2}\alpha + 1}} = \frac{1}{{{{\left( { - 2\sqrt 2 } \right)}^2} + 1}} = \frac{1}{9}\)\( \Rightarrow \cos \alpha = \pm \frac{1}{3}\).
Vì 0° < α < 180° ⇒ sinα > 0 mà \(\tan \alpha = - 2\sqrt 2 \)< 0 nên cosα < 0.
Do đó \(\cos \alpha = - \frac{1}{3}\).
Câu 6:
12/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Vì \(\cot \alpha = - \sqrt 2 \) nên \(\tan \alpha = \frac{1}{{\cot \alpha }} = - \frac{{\sqrt 2 }}{2}\), do đó D đúng.
Do 0° < α < 180° nên sinα > 0.
Ta có: \[{\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\]
\( \Rightarrow {\sin ^2}\alpha = \frac{1}{{{{\cot }^2}\alpha + 1}} = \frac{1}{{{{\left( { - \sqrt 2 } \right)}^2} + 1}} = \frac{1}{3}\)
\( \Rightarrow \sin \alpha = \frac{1}{{\sqrt 3 }}\) nên A đúng.
Lại có: \[\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} \Rightarrow \cos \alpha = \cot \alpha .\sin \alpha = - \sqrt 2 .\frac{1}{{\sqrt 3 }} = - \frac{{\sqrt 6 }}{3}\].
Do đó B sai, C đúng.
Câu 7:
17/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Do 0° < α < 180°, α ≠ 90° nên tanα, cotα cùng dấu và tanα + cotα > 0 nên tanα > 0.
Mà \(\sin \alpha = \frac{2}{5}\) > 0.
Do đó cosα > 0.
Ta có sin2α + cos2α = 1
Suy ra \(\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } = \sqrt {1 - {{\left( {\frac{2}{5}} \right)}^2}} = \frac{{\sqrt {21} }}{5}\).
Câu 8:
22/07/2024Cho \(\cos \alpha = \frac{1}{3}\). Tính \(A = \frac{{\tan \alpha + 4\cot \alpha }}{{\tan \alpha + \cot \alpha }}\).
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có
\(A = \frac{{\tan \alpha + 4\cot \alpha }}{{\tan \alpha + \cot \alpha }}\)\( = \frac{{\tan \alpha + 4.\frac{1}{{\tan \alpha }}}}{{\tan \alpha + \frac{1}{{\tan \alpha }}}}\)\( = \frac{{\frac{{{{\tan }^2}\alpha + 4}}{{\tan \alpha }}}}{{\frac{{{{\tan }^2}\alpha + 1}}{{\tan \alpha }}}}\)
\( = \frac{{{{\tan }^2}\alpha + 4}}{{{{\tan }^2}\alpha + 1}} = \frac{{\frac{1}{{{{\cos }^2}\alpha }} + 3}}{{\frac{1}{{{{\cos }^2}\alpha }}}} = 1 + 3{\cos ^2}\alpha \).
Thay \(\cos \alpha = \frac{1}{3}\) vào biểu thức \(A = 1 + 3.{\left( {\frac{1}{3}} \right)^2} = 1 + 3.\frac{1}{9} = \frac{4}{3}\).
Câu 9:
22/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Vì 0° < α < 90° nên cosα > 0, sinα > 0
Ta có \({\cos ^2}\alpha = \frac{1}{{1 + {{\tan }^2}\alpha }} = \frac{1}{{10}}\)\( \Rightarrow \cos \alpha = \frac{{\sqrt {10} }}{{10}}\)
Lại có \[\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} \Rightarrow \sin \alpha = \tan \alpha .\cos \alpha = 3.\frac{{\sqrt {10} }}{{10}} = \frac{{3\sqrt {10} }}{{10}}\].
Do đó \[P{\rm{ }} = {\rm{ }}cos\alpha {\rm{ }} + {\rm{ }}sin\alpha = \frac{{\sqrt {10} }}{{10}} + \frac{{3\sqrt {10} }}{{10}} = \frac{{2\sqrt {10} }}{5}\].
Câu 10:
17/07/2024Cho góc α (0° < α < 180°) thỏa mãn \(\cos \alpha = \frac{5}{{13}}\).
Giá trị của biểu thức \(P = 2\sqrt {4 + 5\tan \alpha } + 3\sqrt {9 - 12\cot \alpha } \) là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Vì 0° < α < 180° nên sinα > 0
Do đó \(\sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - {{\left( {\frac{5}{{13}}} \right)}^2}} = \frac{{12}}{{13}}\).
Suy ra \(\tan \alpha = \frac{{12}}{5}\); \(\cot \alpha = \frac{5}{{12}}\)
Do đó \(P = 2\sqrt {4 + 5.\frac{{12}}{5}} + 3\sqrt {9 - 12.\frac{5}{{12}}} = 2.4 + 3.2 = 8 + 6 = 14\).
Câu 11:
22/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Do tanα = 5 nên cosα ≠ 0.
Chia cả tử và mẫu của P cho cosα ta được
\(P = \frac{{2\frac{{\sin \alpha }}{{\cos \alpha }} + 3\frac{{\cos \alpha }}{{\cos \alpha }}}}{{3\frac{{\sin \alpha }}{{\cos \alpha }} - 2\frac{{\cos \alpha }}{{\cos \alpha }}}} = \)\(\frac{{2\tan \alpha + 3}}{{3\tan \alpha - 2}} = \frac{{2.5 + 3}}{{3.5 - 2}} = 1\).
Vậy P = 1.
Câu 12:
19/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có P = sin4α – cos4α \( = \left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right).\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = {\sin ^2}\alpha - {\cos ^2}\alpha \).
Do cotα = 3, suy ra sinα ≠ 0.
Chia cả hai vế của biểu thức cho sin2α ta được: \(\frac{P}{{{{\sin }^2}\alpha }} = 1 - {\cot ^2}\alpha \)
\( \Leftrightarrow P\left( {1 + {{\cot }^2}\alpha } \right) = 1 - {\cot ^2}\alpha \)
Thay cotα = 3 vào ta được: P.(1 + 9) = 1 – 9 \( \Leftrightarrow P = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}\).