Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án
Dạng 1: Cách làm các bài tập giải tam giác có đáp án
-
398 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
12/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Từ định lí tổng 3 góc trong tam giác, ta có ˆA=180∘−(ˆB+ˆC)=70∘.
Theo định lí sin, ta có asinA=bsinB=csinC
⇒{b=a.sinBsinA=10.sin50∘sin70∘≈8,15c=a.sinCsinA=10.sin60∘sin70∘≈9,22.
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Theo hệ quả của định lí côsin, ta có:
cosA=b2+c2−a22bc=82+92−722.8.9=23⇒ˆA≈48∘11′.
cosB=a2+c2−b22ac=72+92−822.7.9=1121⇒ˆB≈58∘24′.
Do đó ˆC=180∘−(ˆA+ˆB)≈73∘25′.
Câu 3:
12/07/2024Tam giác ABC có b = 12, c = 15, ˆA=140∘. Khi đó, tìm khẳng định sai trong các khẳng định dưới đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Theo định lý côsin ta có: a2=b2+c2−2bc.cosA.
Thay số ta được: a2=122+152−2.12.15.cos140∘≈644,76
⇒ a ≈ 25,4.
Lại có: cosB=a2+c2−b22ac≈25,42+152−1222.25,4.15≈0,95
⇒ˆB≈17,64∘.
Từ đó, ˆC=180∘−(ˆA+ˆB)≈180∘−(140∘+17,64∘)=22,36∘.
Câu 4:
20/07/2024Cho tam giác ABC biết a = 3, b = 5, c = 7. Tìm khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng hệ quả của định lí côsin, ta có: cosA=b2+c2−a22bc=52+72−322.5.7=1314
⇒ˆA≈21,79∘
Ta có: cosB=a2+c2−b22ac=32+72−522.3.7=1114.
⇒ˆB≈38,21∘.
Do đó: ˆC=180∘−(ˆA+ˆB)≈180∘−(21,79∘+38,21∘)=120∘.
Câu 5:
21/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng định lý côsin ta có:
cosA=b2+c2−a22bc⇔12=b2+122−1622.b.12⇔2b2−224=24b
⇔[b=6+2√37b=6−2√37(loai).
Vậy b = 6 + 2√37.
Lại có: asinA=csinC⇒sinC=sinA.ca=sin60∘.1216=3√38.
⇒ˆC≈40,5∘.
Vậy ˆB=180∘−(ˆA+ˆC)≈180∘−(60∘+40,5∘)=79,5∘.
Câu 6:
20/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Trong tam giác ABC:
ˆA=180∘−(ˆB+ˆC)≈180∘−(43∘42′+16∘20′)=119∘58′.
Theo định lý sin ta có:
asinA=bsinB=csinC
⇒b=a.sinBsinA≈46.sin43∘42′sin119∘58′≈36,68.
Và c=a.sinCsinA≈46.sin16∘20′sin119∘58′≈14,93.
Câu 7:
21/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: ˆB=180∘−(ˆA+ˆC)=180∘−(90∘+23∘)=67∘.
Lại có: asinA=bsinB=csinC
⇒b=a.sinBsinA=20.sin67∘≈18,41.
Và c=a.sinCsinA=20.sin23∘≈7,81.
Câu 8:
12/07/2024Cho tam giác ABC biết AB = 3, AC=3√2 và ˆC=45∘. Trong các phương án dưới đây, chọn phương án SAI?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có: AB2=AC2+BC2−2.AC.BC.cos45∘
⇔32=(3√2)2+BC2−2.BC.3√2.√22
⇔BC2−6BC+9=0
⇔ (BC – 3)2 = 0
⇒ BC = 3.
Dễ thấy AB2 + BC2 = AC2 nên theo định lý đảo của định lý Pythagore suy ra tam giác ABC vuông tại B.
Vậy ˆB=90∘, ˆA=45∘.
Câu 9:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Từ AB : AC = 3 : 4⇒AB3=AC4.
Đặt AB3=AC4=k, k > 0 ⇒ AB = 3k; AC = 4k.
Ta có: 1AH2=1AB2+1AC2⇔1242=19k2+116k2⇔k = 10.
Suy ra: AB = 30; AC = 40, từ đó suy ra BC = 50 (định lí Pythagore).
Lại có: cos B = ABBC=3050=35⇒ˆB≈53,13∘
⇒ˆC=90∘−ˆB≈36,87∘.
Câu 10:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: cos A = b2+c2−a22bc= 172+202−1622.17.20= 433680
⇒ˆA= 50,45∘.
Tương tự: cos B = a2+c2−b22ac= 162+202−1722.16.20= 367640
⇒ˆB≈55∘
Do đó: ˆC=180∘−(ˆA+ˆB)≈180∘−(50,45∘+55∘)=74,55∘.
Câu 11:
17/07/2024 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Trong tam giác ABC có: ˆB=180∘−(ˆA+ˆC)=180∘−(30∘+45∘)=105∘.
Theo định lý sin ta có: asinA=bsinB=csinC
Do đó: a = c.sinAsinC= 7,2.sin30∘sin45∘= 18√25.
Và b = c.sinBsinC= 7,2.sin105∘sin45∘= 18+18√35.
Câu 12:
23/07/2024Cho hình thoi ABCD có cạnh bằng 2 cm và ^ABC=60∘. Tìm khẳng định SAI trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
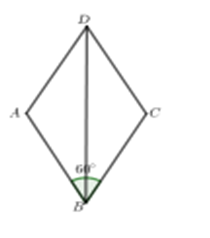
Vì ^ABC=60∘ nên ^BAD=120∘.
Ta có ABCD là hình thoi nên AB = AD = 2 cm.
Lại có BD là tia phân giác của góc ^ABC nên ^ABD=12^ABC=12.60∘=30∘.
Mà AB = AD nên tam giác ABD cân tại A.
Do đó: ^ADB=^ABD=30∘ và ^BAD=180∘−2^ABD=180∘−2.30∘=120∘.
Áp dụng định lí côsin trong tam giác ABD ta có:
BD2=AB2+AD2−2.AB.AD.cos^BAD
Thay số: BD2=22+22−2.2.2.cos120∘=12⇒BD=2√3cm.
Bài thi liên quan
-
Dạng 2: Áp dụng giải tam giác vào các bài toán thực tế có đáp án
-
12 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Thi Online Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án (1211 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 2. Định lý côsin và định lý sin có đáp án (817 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án (397 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Toán 10 CTST Bài 2. Hàm số bậc hai có đáp án (2638 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án (2526 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 1: Mệnh đề có đáp án (1410 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án (1156 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án (1095 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 1. Số gần đúng và sai số có đáp án (1063 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 1. Hàm số và đồ thị có đáp án (917 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 2: Tập hợp có đáp án (890 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 2: Hệ bất phương trình bậc nhất hai ẩn có đáp án (866 lượt thi)
- Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Các số đặc trưng đo xu thế trung tâm của mẫu số liệu có đáp án (766 lượt thi)
