Thi Online Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án
Dạng 2: Áp dụng giải tam giác vào các bài toán thực tế có đáp án
-
329 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Tính khoảng cách giữa hai điểm ở hai đầu của một ao cá nhà bác An. Biết khoảng cách từ chỗ bác An đứng đến hai đầu ao lần lượt là 700 m và 900 m và bác An quan sát nhìn hai điểm này dưới một góc 60° như hình vẽ.
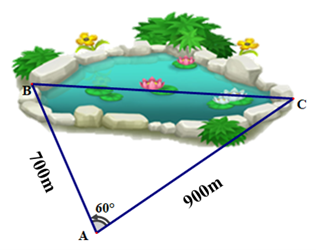
Xem đáp án
Hướng dẫn giải:
Theo định lí côsin ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cosA\)
\( = {700^2} + {900^2} - 2.700.900.cos60^\circ \)= 670 000.
Suy ra: BC = \(\sqrt {670000} \approx 818,5\)(m).
Câu 2:
22/07/2024Từ vị trí điểm C người ta quan sát một cây cao (như hình vẽ).
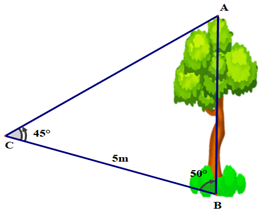
Biết BC = 5 m, \(\widehat {ACB} = 45^\circ ,\widehat {CBA} = 50^\circ \). Chiều cao của cây bằng bao nhiêu?
Xem đáp án
Hướng dẫn giải:
Áp dụng định lí tổng 3 góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)\( \Rightarrow \widehat A = 85^\circ \).
Theo định lí sin ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)\( \Leftrightarrow \frac{{AB}}{{\sin 45^\circ }} = \frac{5}{{\sin 85^\circ }}\)\( \Leftrightarrow AB = \sin 45^\circ .\frac{5}{{\sin 85^\circ }}\)≈ 3,55 (m).
Vậy chiều cao của cây khoảng 3,55 m.
Câu 3:
23/07/2024Khoảng cách từ A đến B không thể đo trực tiếp vì phải qua một đầm lầy nên người ta làm như sau: Xác định một điểm C sao cho ta đo được AC = 15 m, BC = 21 m và \[\widehat {ACB} = 80^\circ \]. Khoảng cách AB gần nhất với kết quả nào dưới đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta mô phỏng bài toán như hình vẽ sau:
Theo định lí côsin ta có:
\(A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\).
Thay số: \(A{B^2} = {21^2} + {15^2} - 2.21.15.\cos 80^\circ \)≈ 556,6
Suy ra: AB ≈ \(\sqrt {556,6} \)≈ 23,6 (m).
Vậy khoảng cách AB là khoảng 23,6 m và gần nhất với kết quả 24 m.
Câu 4:
19/07/2024Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc \(\widehat {COD} = 60^\circ \).
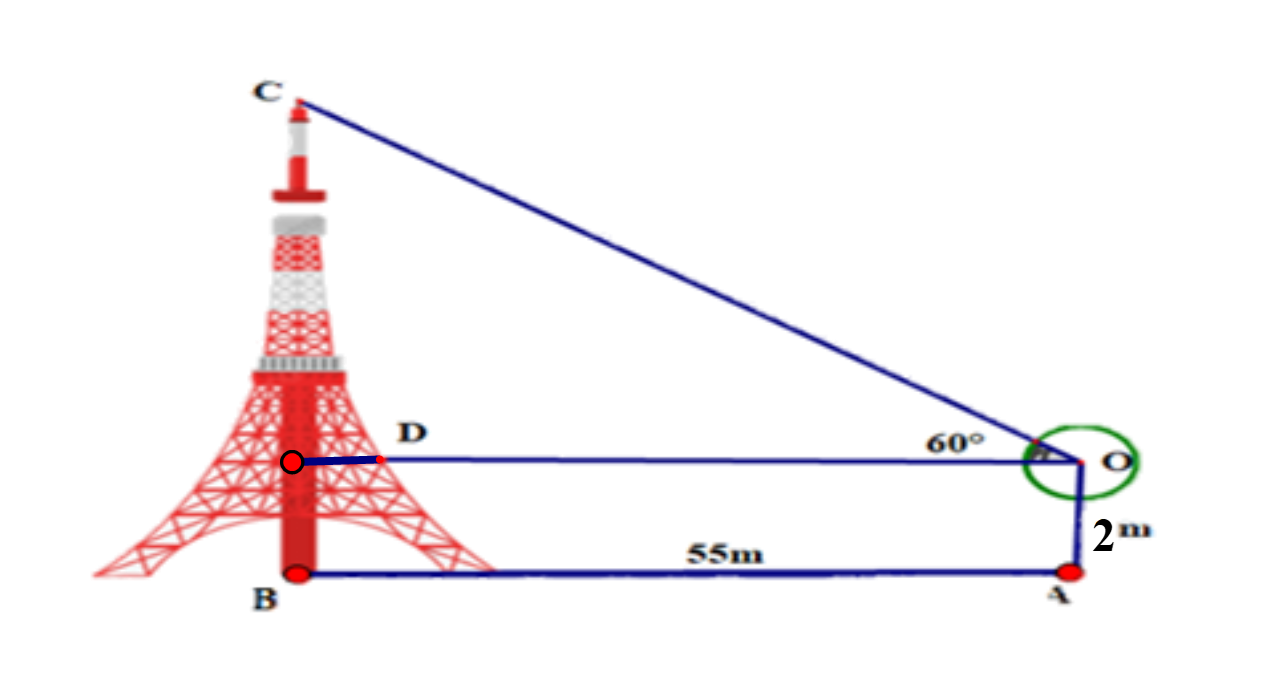
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét tam giác OCD vuông tại D có OD = AB = 55 (m); \(\widehat {COD} = 60^\circ \)
Nên CD = OD. tan\(\widehat {COD}\) = 55\(\sqrt 3 \)≈ 95,26 (m).
Vậy chiều cao của tháp là: 95,26 + 2 = 97,26 (m).
Câu 5:
20/07/2024Từ hai điểm A và B của một tòa nhà, người ta quan sát điểm pháo hoa nổ. Biết rằng AB = 120 m, phương nhìn AC tạo với phương ngang một góc 45°, phương nhìn BC tạo với phương ngang góc 15°30'.
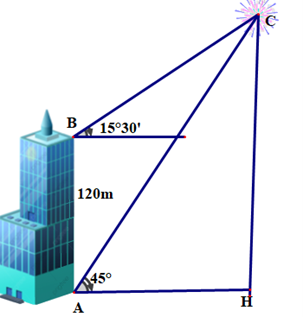
Hỏi điểm pháo hoa nổ cao so với mặt đất gần với giá trị nào sau đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có: \(\widehat {BAC} = \widehat {BAH} - \widehat {CAH} = 90^\circ - 45^\circ = 45^\circ \).
Lại có: \(\widehat {ABC} = 90^\circ + 15^\circ 30' = 105^\circ 30'\).
Trong tam giác ABC có: \(\widehat {BCA} = 180^\circ - \left( {\widehat {BAC} + \widehat {ABC}} \right) = 29^\circ 30'\).
Áp dụng định lí sin vào ∆ABC ta có:
\(\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{AB}}{{\sin \widehat {BCA}}}\)\( \Rightarrow \)AC = \(\sin \widehat {ABC}.\frac{{AB}}{{\sin \widehat {BCA}}}\)≈ 234,83 (m).
Trong tam giác vuông AHC có: \(\frac{{CH}}{{AC}} = \sin 45^\circ \)\( \Rightarrow \)CH = AC. sin 45° ≈ 166,05.
Vậy điểm pháo hoa nổ cao so với mặt đất khoảng 166,05 m.
Câu 6:
16/07/2024Hai chiếc tàu thủy M và N cách nhau 500 m. Từ M và N thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta thấy chiều cao AB của tháp dưới một góc \(\widehat {AMB} = 30^\circ \); \(\widehat {ANB} = 45^\circ \).
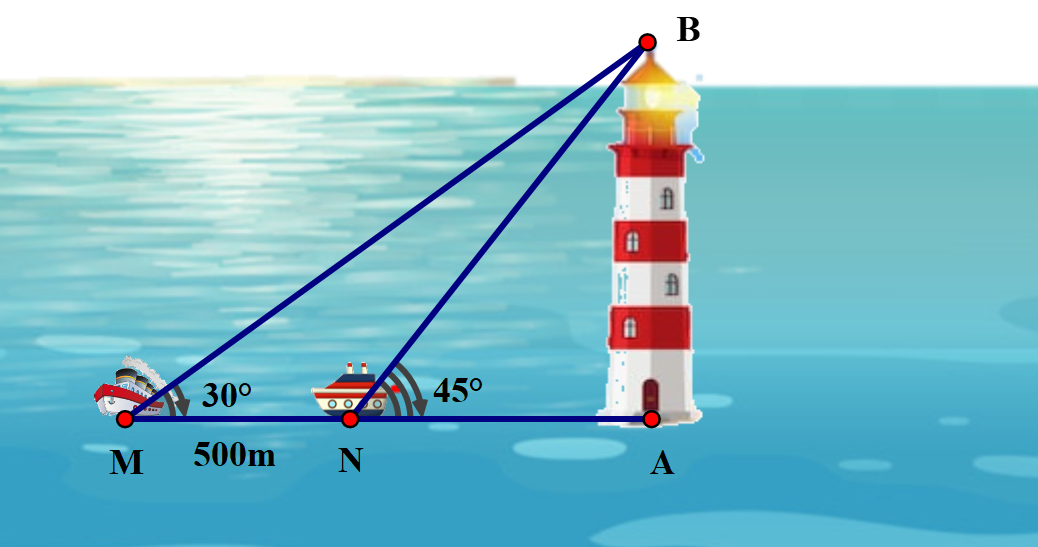
Tính chiều cao AB của tháp.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
\(\widehat {MNB} = 180^\circ - \widehat {BNA} = 135^\circ \)\( \Rightarrow \widehat {MBN} = 180^\circ - \widehat {BNM} - \widehat {BMN} = 15^\circ \)
Áp dụng định lí sin vào tam giác BMN ta có:
\(\frac{{MN}}{{\sin \widehat {MBN}}} = \frac{{BN}}{{\sin \widehat {BMN}}}\)\( \Rightarrow BN = \sin \widehat {BMN}.\frac{{MN}}{{\sin \widehat {MBN}}}\) ≈ 965,92 (m)
Xét tam giác BNA vuông tại A có: AB = BN. sin \(\widehat {BNA}\) ≈ 683 (m).
Câu 7:
20/07/2024Người ta muốn xây dựng một tuyến đường hầm qua một ngọn núi để các em vùng cao đi học được dễ hơn (như hình dưới).
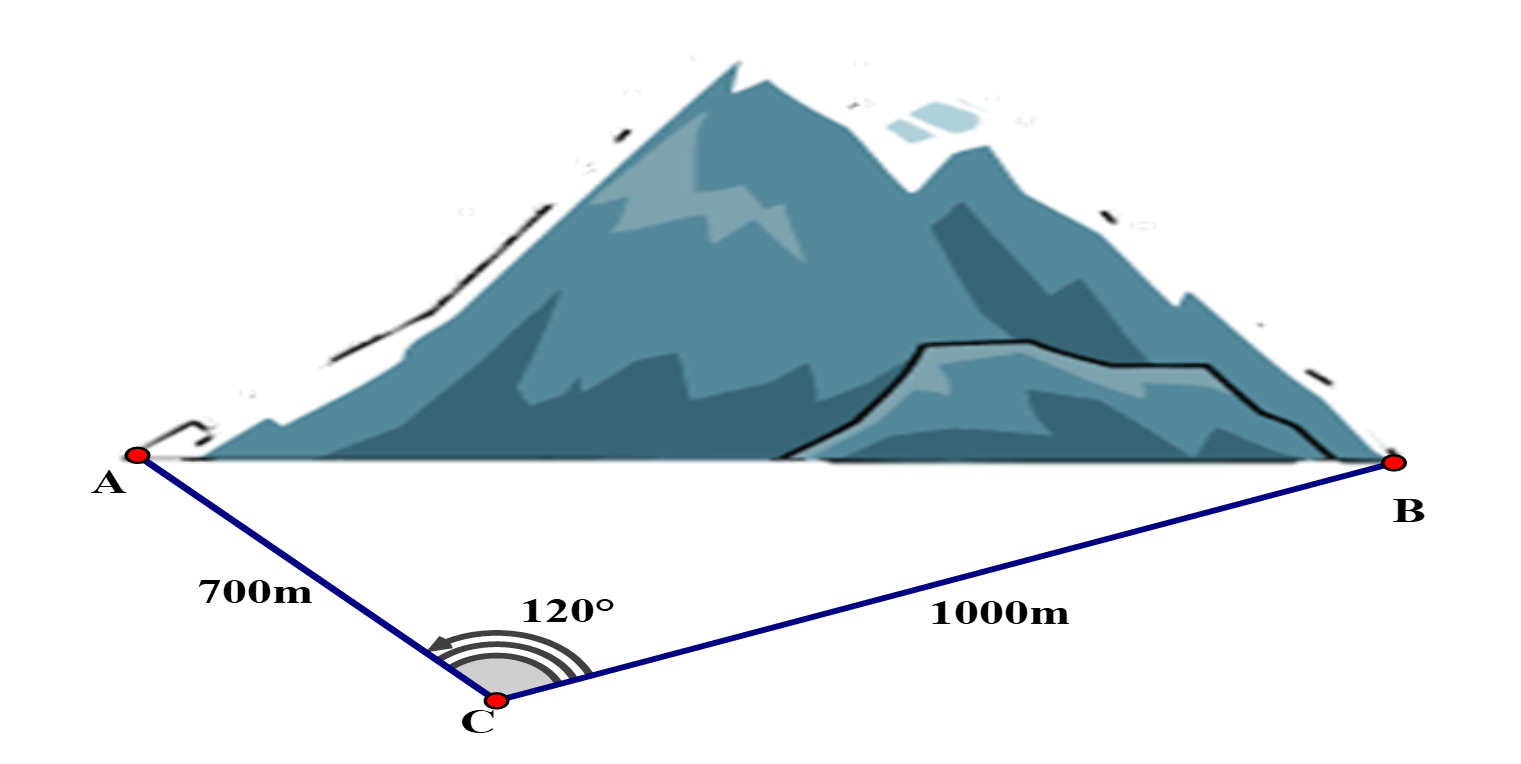
Độ dài đường hầm AB gần với kết quả nào dưới đây nhất?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng định lí côsin trong ∆ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2AC.BC.\cos \widehat C = 2\,190\,000\)
\( \Rightarrow AB = \sqrt {2\,\,190\,\,000} \approx 1479,86\left( m \right)\)
Độ dài đường hầm AB là: 1479,86 m.
Câu 8:
17/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta mô phỏng bài toán như hình vẽ sau:
Áp dụng định lí côsin ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\)
\( \Leftrightarrow 144 = A{B^2} + 64 - 16.AB.\cos 65^\circ \)
\[ \Leftrightarrow A{B^2} - 16.AB.\cos {65^o} - 80 = 0 \Leftrightarrow \left[ \begin{array}{l}AB \approx 13\\AB \approx - 6,18\,\,(L)\end{array} \right.\]
Do đó: AB = 13 km.
Ta có: AC + BC – AB = 12 + 8 – 13 = 7 (km)
Vậy số tiền phải tốn thêm 7 . 150 000 = 1 050 000 (đồng).
Câu 9:
13/07/2024Một người đi tàu điện từ trạm A đến trạm B. Khi đứng ở trạm A, người đó nhìn thấy một tháp C. Hướng nhìn từ người đó đến tháp tạo với hướng đi của tàu một góc 60°. Khi xe dừng ở trạm B, người đó vẫn thấy được tháp C, hướng nhìn từ người đó đến tháp ngược với hướng đi của tàu một góc 45°. Biết rằng đoạn đường tàu đi từ trạm A đến trạm B dài 10 km.
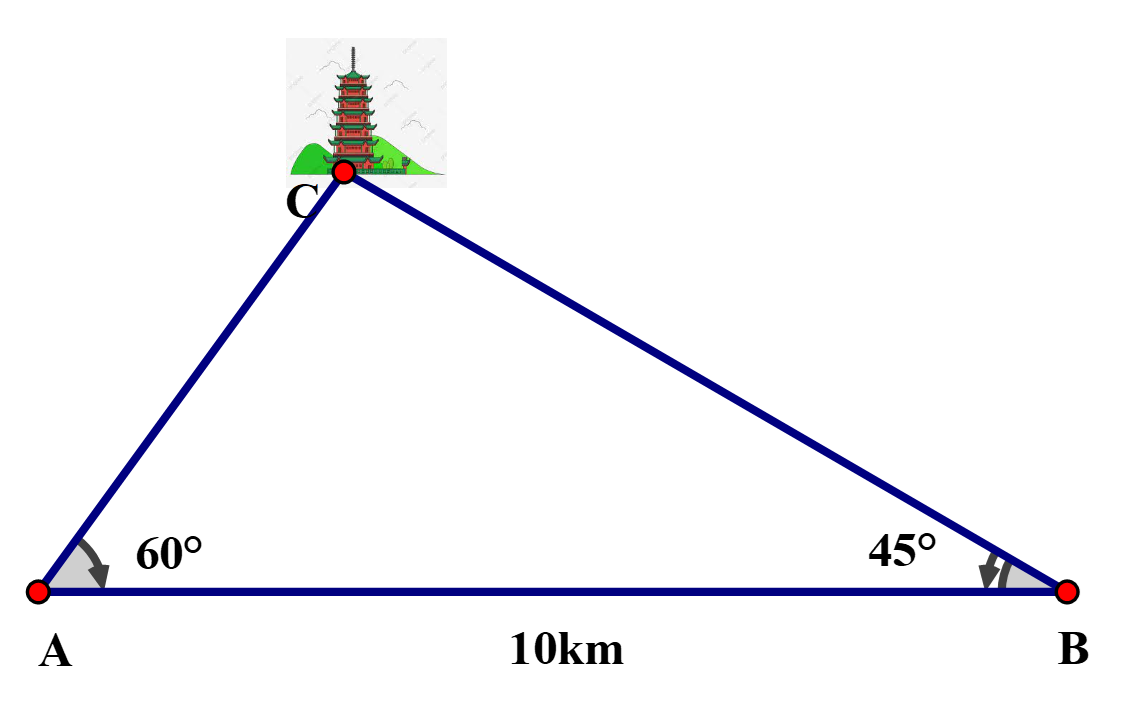
Khoảng cách từ trạm A đến tháp C là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Trong tam giác ABC có: \(\widehat C = 180^\circ - \widehat A - \widehat B = 75^\circ \).
Theo định lý sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)\( \Leftrightarrow \)AC = \(\frac{{AB.\sin B}}{{\sin C}}\)= \(\frac{{10.\sin 45^\circ }}{{\sin 75^\circ }}\)= −10 + 10\(\sqrt 3 \).
Vậy khoảng cách từ trạm A đến tháp C là −10 + 10\(\sqrt 3 \) km.
Câu 10:
21/07/2024Từ vị trí A, người ta quan sát một cây thông. Biết AH = 5 m, HB = 15 m, \(\widehat {BAC} = 45^\circ \).
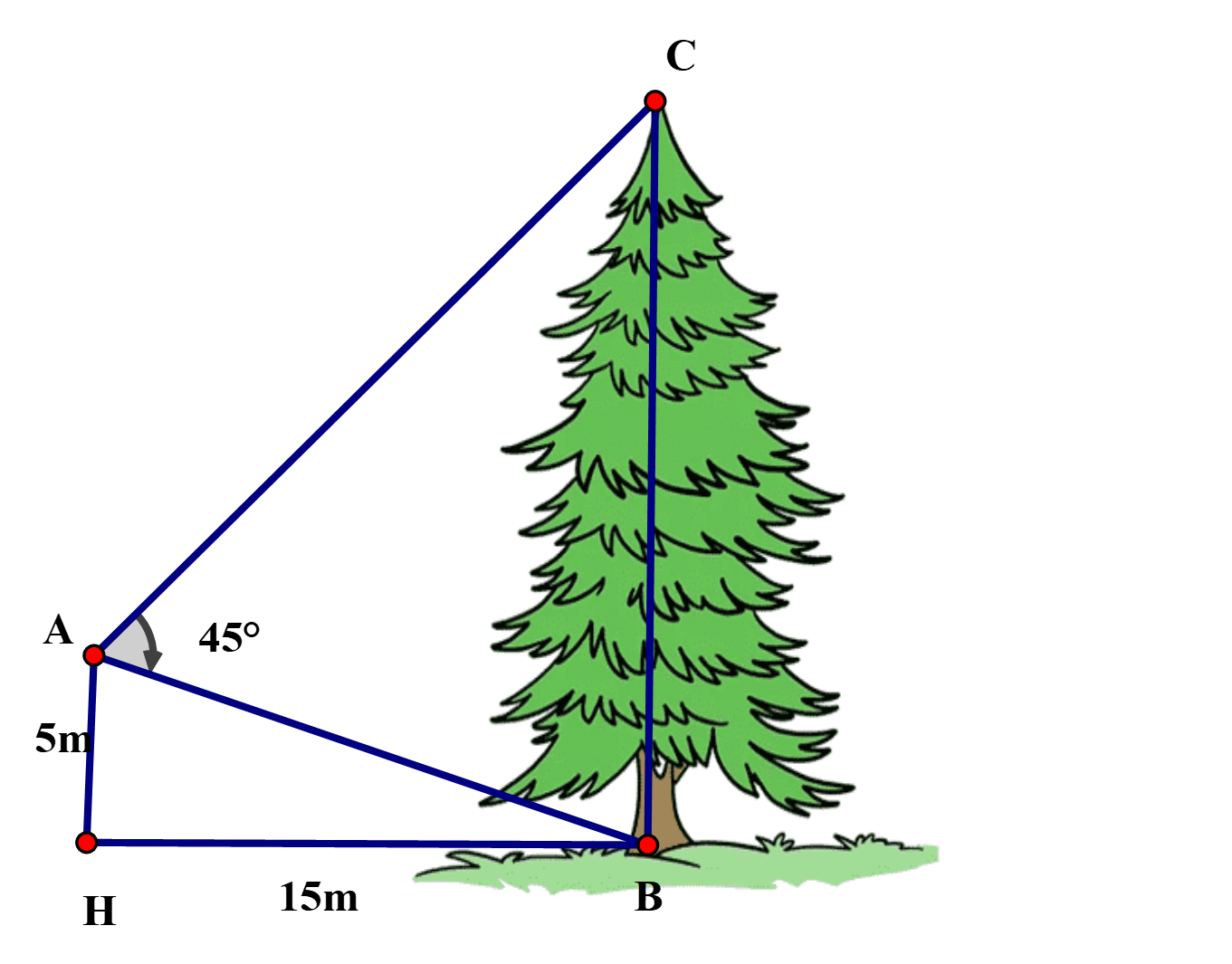
Chiều cao của cây bằng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Trong tam giác ABH vuông tại H ta có:
\[{\rm{AB}}\,{\rm{ = }}\,\sqrt {A{H^2} + H{B^2}} = \sqrt {{5^2} + {{15}^2}} = 5\sqrt {10} \].
Lại có: tan \(\widehat {ABH}\)= \(\frac{{AH}}{{HB}}\)= \(\frac{1}{3}\)\( \Rightarrow \)\(\widehat {ABH}\)≈18,43°.
\(\widehat {ABC} = 90^\circ - \widehat {ABH} \approx 71,57^\circ \) \( \Rightarrow \widehat {ACB} = 180^\circ - \widehat {CAB} - \widehat {ABC} \approx 63,43^\circ \).
Theo định lý sin trong tam giác ABC ta có:
\(\frac{{CB}}{{\sin \widehat {CAB}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\) \( \Rightarrow \)CB ≈ \[\frac{{5\sqrt {10} .\sin 45^\circ }}{{\sin 63,43^\circ }}\]≈12,5.
Chiều cao của cây khoảng 12,5 m.
Câu 11:
19/07/2024Để đo chiều cao của tháp có đỉnh A, chân tháp là B, người ta đứng dưới mặt đất quan sát ở hai điểm C và D sao cho B, C, D thẳng hàng (như hình vẽ).
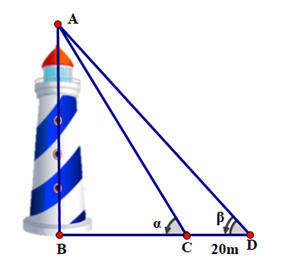
Qua đo đạc, ta thu được DC = 20 m, α = 58°; β = 47°. Chiều cao của tháp gần nhất với kết quả nào dưới đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có: \(\widehat {ACD} = 180^\circ - \alpha = 122^\circ \)\( \Rightarrow \widehat {CAD} = 180^\circ - \widehat {ACD} - \widehat {ADC} = 11^\circ \).
Theo định lý sin trong tam giác ADC ta có: \(\frac{{AC}}{{\sin \widehat {CDA}}} = \frac{{CD}}{{\sin \widehat {CAD}}}\)
\( \Rightarrow \)AC = \(\frac{{CD.\sin \widehat {CDA}}}{{\sin \widehat {CAD}}}\)≈ 76,66 m.
Trong tam giác ABC có: \(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\)
\( \Rightarrow \)AB = \(\frac{{AC.\sin \widehat {ACB}}}{{\sin \widehat {ABC}}}\) ≈\(\frac{{76,66.\sin 58^\circ }}{{\sin 90^\circ }}\) ≈ 65 m.
Vậy chiều cao của tháp là 65 m.
Câu 12:
20/07/2024Hình dưới đây vẽ một trường học nọ nằm ở vị trí A là góc tạo bởi hai con đường.
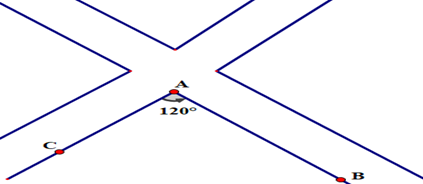
Nhà bạn An ở vị trí B cách trường 5 km, nhà bạn Hòa ở vị trí C cách trường 4 km . Biết \(\widehat {BAC} = 120^\circ \). Hỏi khoảng cách từ nhà bạn An đến nhà bạn Hòa (theo đường chim bay) gần với đáp án nào nhất?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Trong tam giác ABC, áp dụng định lý côsin ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
\( \Rightarrow B{C^2} = {4^2} + {5^2} - 2.4.5.\cos 120^\circ = 61\)
\( \Rightarrow BC = \sqrt {61} \approx 7,81\).
Hỏi khoảng cách từ nhà bạn An đến nhà bạn Hòa (theo đường chim bay) gần bằng 7,81 km.