28 câu hỏi trắc nghiệm thuộc Giải SBT Toán 11 Cánh Diều Bài tập cuối chương VI

Nếu $a^{\frac{3}{4}} < a^{\frac{4}{5}}$ thì:

A. a < 1;

B. 0 < a < 1;

C. a < 0;

D. a > 1.

Đáp án đúng là: D

Do $\frac{3}{4} < \frac{4}{5}$ và $a^{\frac{3}{4}} < a^{\frac{4}{5}}$ suy ra a > 1.

Câu 2:

Nếu 2^x = 3 thì 4^x bằng:

A. 6;

B. 9;

C. 12;

D. 8.

Đáp án đúng là: B

Ta có: $4^{x} = {(2^{2})}^{x} = {(2^{x})}^{2} = 3^{2} = 9.$

Câu 3:

14/07/2024

Nếu $\sqrt[6]{x} = a$ thì $\sqrt{x}$ bằng:

A. $\sqrt[3]{a};$

B. $\sqrt[4]{a};$

C. a³;

D. a⁴.

Đáp án đúng là: C

Ta có: $\sqrt{x} = x^{\frac{1}{2}} = x^{\frac{3}{6}} = {(\sqrt[6]{x})}^{3} = a^{3} .$

Câu 4:

15/07/2024

Rút gọn biểu thức $\sqrt{\sqrt[3]{x}}$ với x ≥ 0 nhận được:

A. $\sqrt[6]{x};$

B. $x^{\frac{1}{5}};$

C. $\sqrt[5]{x};$

D. $x^{\frac{1}{6}} .$

Đáp án đúng là: A

Với x ≥ 0 ta có: $\sqrt{\sqrt[3]{x}} = \sqrt[2 \cdot 3]{x} = \sqrt[6]{x} .$

Câu 5:

Tập xác định của hàm số $y = {(\sqrt{2})}^{x + 2}$ là:

A. (2; +∞);

B. ℝ;

C. (2; +∞) \ {–1};

D. ℤ.

Đáp án đúng là: B

Ta có: $\sqrt{2} > 0$ và $\sqrt{2} \neq 1$ nên hàm số $y = {(\sqrt{2})}^{x + 2}$ là hàm số mũ có tập xác định là R

Câu 6:

Tập xác định của hàm số log₂(x – 1) là:

A. [1; +∞);

B. [1; +∞) \ {2};

C. (1; +∞);

D. (0; +∞).

Đáp án đúng là: C

Điều kiện: x – 1 > 0 hay x > 1.

Suy ra tập xác định của hàm số log₂(x – 1) là (1; +∞).

Câu 7:

Giá trị của log₂9 – log₂36 bằng:

A. 2;

B. 4;

C. – 4;

D. – 2.

Đáp án đúng là: D

Ta có: $\log_{2} 9 - \log_{2} 36 = \log_{2} \frac{9}{36}$ $= \log_{2} \frac{1}{4} = \log_{2} 2^{- 2} = - 2.$

Câu 8:

23/07/2024

Nếu $\log_{4} \sqrt{a} = 16$ thì log₄a bằng:

A. 32;

B. 256;

C. 8;

D. 4.

Đáp án đúng là: A

Với a > 0 ta có: $\log_{4} a = \log_{4} {(\sqrt{a})}^{2} = 2 \log_{4} \sqrt{a} = 2 \cdot 16 = 32.$

Câu 9:

19/07/2024

Nếu log2 = a thì log 4 000 bằng:

A. 2a + 3;

B. 3a²;

C. $\frac{1}{2} a + 3;$

D. a² + 3.

Đáp án đúng là: A

Ta có: log4 000 = log(4.1 000) = log(2².10³)

= log2² + log10³ = 2log2 + 3 = 2a + 3.

Câu 10:

Nếu log₁₂6 = a thì log₂6 bằng:

A. $\frac{a}{1 + a};$

B. $\frac{2 a}{1 - a};$

C. $\frac{a}{1 - a};$

D. $\frac{2 a}{1 + a} .$

Đáp án đúng là: C

Ta có: $\log_{2} 6 = \frac{\log_{12} 6}{\log_{12} 2} = \frac{\log_{12} 6}{\log_{12} (\frac{12}{6})}$ $= \frac{\log_{12} 6}{\log_{12} 12 - \log_{12} 6} = \frac{a}{1 - a} .$

Câu 11:

Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. $y = {(\frac{e}{π})}^{x};$

B. $y = {(\sqrt{3})}^{x}$

C. y = log_0,3x;

D. y = –log₂x.

Đáp án đúng là: B

− Hàm số mũ $y = {(\sqrt{3})}^{x}$ đồng biến trên ℝ vì $\sqrt{3} > 1.$

− Ba hàm số còn lại nghịch biến trên tập xác định của chúng.

⦁ Hàm số mũ $y = {(\frac{e}{π})}^{x}$ nghịch biến trên ℝ vì $0 < \frac{e}{π} < 1.$

⦁ Hàm số lôgarit y = log_0,3x nghịch biến trên (0; +∞) vì 0 < 0,3 < 1.

⦁ Hàm số lôgarit $y = - \log_{2} x = \log_{\frac{1}{2}} x$ nghịch biến trên (0; +∞) vì $0 < \frac{1}{2} < 1.$

Câu 12:

Nghiệm của phương trình 3^{x – 1} = 1 là:

A. x = 1;

B. x = 0;

C. x = 2;

D. x = – 1.

Đáp án đúng là: A

Ta có: 3^{x – 1} = 1 ⇔ 3^{x – 1} = 3⁰ ⇔ x – 1 = 0 ⇔ x = 1.

Vậy phương trình có nghiệm x = 1.

Câu 13:

19/07/2024

Nghiệm của phương trình $0, 5^{x} = {(\sqrt{2})}^{x + 3}$ là:

A. x = 3;

B. x = 1;

C. x = – 3;

D. x = – 1.

Đáp án đúng là: D

Ta có: $0, 5^{x} = {(\sqrt{2})}^{x + 3} \Leftrightarrow {(2^{- 1})}^{x} = {(2^{\frac{1}{2}})}^{x + 3}$

$\Leftrightarrow 2^{- x} = 2^{\frac{x + 3}{2}} \Leftrightarrow - x = \frac{x + 3}{2}$

⇔ −2x = x + 3 ⇔ 3x + 3 = 0

⇔ x = –1.

Vậy phương trình có nghiệm x = – 1.

Câu 14:

Nghiệm của phương trình $\log_{\frac{1}{3}} x = - 2$ là:

A. $x = - \frac{1}{9};$

B. $x = \frac{1}{9} .$

C. x = 9;

D. x = – 9.

Đáp án đúng là: C

Ta có: $\log_{\frac{1}{3}} x = - 2 \Leftrightarrow x = {(\frac{1}{3})}^{- 2} = 9.$

Vậy phương trình có nghiệm x = 9.

Câu 15:

Nghiệm của phương trình $\log_{5} (2 x - 3) - \log_{\frac{1}{5}} (2 x - 3) = 0$ là

A. $x = \frac{3}{2};$

B. x = 8;

C. x = 2;

D. x = 1.

Đáp án đúng là: C

Ta có: $\log_{5} (2 x - 3) - \log_{\frac{1}{5}} (2 x - 3) = 0$

$\Leftrightarrow \log_{5} (2 x - 3) - \log_{5^{- 1}} (2 x - 3) = 0$

⇔ log₅ (2x – 3) + log₅ (2x – 3) = 0

⇔ 2log₅ (2x – 3) = 0

⇔ log₅ (2x – 3) = 0

⇔ 2x – 3 = 5⁰

⇔ 2x – 3 = 1 ⇔ x = 2.

Vậy phương trình có nghiệm x = 2.

Câu 16:

Tập nghiệm của bất phương trình $2^{\sqrt{x}} > 1$ là:

A. (0; +∞);

B. [0; +∞);

C. ℝ;

D. ℝ \ {0}.

Đáp án đúng là: A

Điều kiện: x ≥ 0.

Ta có: $2^{\sqrt{x}} > 1 \Leftrightarrow 2^{\sqrt{x}} > 2^{0} \Leftrightarrow \sqrt{x} > 0 \Leftrightarrow x > 0.$

Kết hợp với điều kiện x ≥ 0 suy ra: x > 0.

Vậy tập nghiệm của bất phương trình là (0; +∞).

Câu 17:

17/07/2024

Tập nghiệm của bất phương trình log₂(3x – 1) < 3 là:

A. (– ∞; 3);

B. $(\frac{1}{3}; 3);$

C. $(- \infty; \frac{10}{3});$

D. $(\frac{1}{3}; \frac{10}{3}) .$

Đáp án đúng là: B
Ta có: log₂(3x – 1) < 3 ⇔ 0 < 3x – 1 < 2³ ⇔ 0 < 3x – 1 < 8
$\Leftrightarrow \{\begin{cases} 3 x - 1 > 0 \\ 3 x - 1 < 8 \end{cases} \Leftrightarrow \{\begin{cases} x > \frac{1}{3} \\ x < 3 \end{cases} \Leftrightarrow \frac{1}{3} < x < 3.$
Vậy tập nghiệm của bất phương trình là:

Câu 18:

Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = a^x, y = b^x, y = c^x được cho bởi Hình 5. Kết luận nào sau đây là đúng đối với ba số a, b, c?

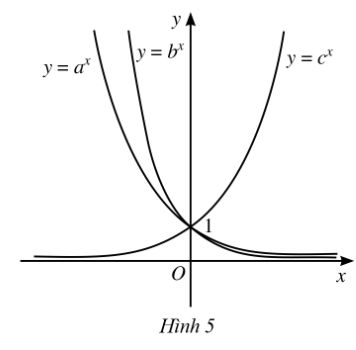
Media VietJack

A. c < a < b;

B. c < b < a;

C. a < b < c;

D. b < a < c.

Đáp án đúng là: D

Dựa vào đồ thị ta có:

Hàm số mũ y = c^x đồng biến trên ℝ. Suy ra c > 1.

Hàm số mũ y = a^x và y = b^x nghịch biến trên ℝ. Suy ra 0 < a < 1 và 0 < b < 1.

Thay x = 100 vào hàm số y = a^x và y = b^x ta thấy: a¹⁰⁰ > b¹⁰⁰ > 0. Suy ra 0 < b < a.

Vậy b < a < c.

Câu 19:

Cho a là số thực dương. Viết các biểu thức sau về lũy thừa cơ số a:
a)

a^{\sqrt{3}} . {(\frac{1}{a})}^{\sqrt{3} - 1};

{(a^{\sqrt{5}})}^{2 \sqrt{5}};

{(\frac{1}{a})}^{2 \sqrt{2}} . \sqrt[4]{a^{4 \sqrt{2}}};

a^{π} . \sqrt[3]{a^{3} : a^{6 π}} .

Với a > 0 ta có:
a)

a^{\sqrt{3}} . {(\frac{1}{a})}^{\sqrt{3} - 1} = a^{\sqrt{3}} . {(a^{- 1})}^{\sqrt{3} - 1}

= a^{\sqrt{3}} . a^{1 - \sqrt{3}} = a^{\sqrt{3} + 1 - \sqrt{3}} = a^{1} = a .

{(a^{\sqrt{5}})}^{2 \sqrt{5}} = a^{\sqrt{5} .2 \sqrt{5}} = a^{10} .

{(a^{\sqrt{5}})}^{2 \sqrt{5}} = a^{\sqrt{5} .2 \sqrt{5}} = a^{10} .

= a^{- 2 \sqrt{2}} . a^{\sqrt{2}} = a^{- 2 \sqrt{2} + \sqrt{2}} = a^{- \sqrt{2}} .

a^{π} . \sqrt[3]{a^{3} : a^{6 π}} = a^{π} . \sqrt[3]{a^{3 - 6 π}} = a^{π} . a^{\frac{3 - 6 π}{3}}

= a^{π} . a^{1 - 2 π} = a^{π + 1 - 2 π} = a^{1 - π} .

Câu 20:

Cho x, y là các số thực dương khác 1. Rút gọn các biểu thức sau:
a)

A = \frac{x^{3 \sqrt{3}} - 1}{x^{\sqrt{3}} - 1} - \frac{x^{2 \sqrt{3}} + x^{\sqrt{3}}}{x^{\sqrt{3}}};

B = \frac{x^{2 \sqrt{2}} - y^{2 \sqrt{3}}}{{(x^{\sqrt{2}} - y^{\sqrt{3}})}^{2}} + 1.

Tìm tập xác định của các hàm số sau:
a)

Với x > 0, y > 0, x, y ≠ 1 ta có:
a)

A = \frac{x^{3 \sqrt{3}} - 1}{x^{\sqrt{3}} - 1} - \frac{x^{2 \sqrt{3}} + x^{\sqrt{3}}}{x^{\sqrt{3}}}

= \frac{{(x^{\sqrt{3}})}^{3} - 1^{3}}{x^{\sqrt{3}} - 1} - \frac{{(x^{\sqrt{3}})}^{2} + x^{\sqrt{3}}}{x^{\sqrt{3}}}

= \frac{(x^{\sqrt{3}} - 1) [{(x^{\sqrt{3}})}^{2} + x^{\sqrt{3}} + 1]}{x^{\sqrt{3}} - 1} - \frac{x^{\sqrt{3}} (x^{\sqrt{3}} + 1)}{x^{\sqrt{3}}}

= x^{2 \sqrt{3}} + x^{\sqrt{3}} + 1 - x^{\sqrt{3}} - 1

= x^{2 \sqrt{3}} .

B = \frac{x^{2 \sqrt{2}} - y^{2 \sqrt{3}}}{{(x^{\sqrt{2}} - y^{\sqrt{3}})}^{2}} + 1 = \frac{{(x^{\sqrt{2}})}^{2} - {(y^{\sqrt{3}})}^{2}}{{(x^{\sqrt{2}} - y^{\sqrt{3}})}^{2}} + 1

= \frac{(x^{\sqrt{2}} - y^{\sqrt{3}}) (x^{\sqrt{2}} + y^{\sqrt{3}})}{{(x^{\sqrt{2}} - y^{\sqrt{3}})}^{2}} + 1

= \frac{x^{\sqrt{2}} + y^{\sqrt{3}}}{x^{\sqrt{2}} - y^{\sqrt{3}}} + 1

= \frac{x^{\sqrt{2}} + y^{\sqrt{3}} + x^{\sqrt{2}} - y^{\sqrt{3}}}{x^{\sqrt{2}} - y^{\sqrt{3}}}

= \frac{2 x^{\sqrt{2}}}{x^{\sqrt{2}} - y^{\sqrt{3}}} .

Câu 21:

18/07/2024

y = \frac{2^{x} - 3}{2^{x} + 3};

y = \sqrt{3^{x} - 1};

y = \frac{\log_{2} x}{3 - \log_{2} x};

y = \frac{1}{\sqrt{\log_{0, 2} x + 2}} .

a) Điều kiện: 2x + 3 ≠ 0 (luôn đúng)
Suy ra: Hàm số

y = \frac{2^{x} - 3}{2^{x} + 3}

có tập xác định là ℝ.
b) Điều kiện: 3x – 1 ≥ 0 ⇔ 3x ≥ 1 ⇔ 3x ≥ 30 ⇔ x ≥ 0 (vì 3 > 1)
Suy ra: Hàm số

y = \sqrt{3^{x} - 1}

có tập xác định là [0; + ∞).
c) Điều kiện:

\{\begin{cases} x > 0 \\ 3 - \log_{2} x \neq 0 \end{cases}

\Leftrightarrow \{\begin{cases} x > 0 \\ \log_{2} x \neq 3 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ x \neq 2^{3} \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ x \neq 8 \end{cases} .

Suy ra: Hàm số

y = \frac{\log_{2} x}{3 - \log_{2} x}

có tập xác định là (0; + ∞) \ {8}.
d) Điều kiện:

\{\begin{cases} x > 0 \\ \log_{0, 2} x + 2 > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ \log_{0, 2} x > - 2 \end{cases}

\Leftrightarrow \{\begin{cases} x > 0 \\ x < 0, 2^{- 2} \end{cases}

(vì 0 < 0,2 < 1)

\Leftrightarrow \{\begin{cases} x > 0 \\ x < 25 \end{cases} \Leftrightarrow 0 < x < 25.

Suy ra: Hàm số

y = \frac{1}{\sqrt{\log_{0, 2} x + 2}}

có tập xác định là (0; 25).

Câu 22:

23/07/2024

Cho b > 0 và $b^{\frac{2}{3}} = a .$ Viết b²; $\sqrt{a} \cdot b;$ $\frac{a^{6}}{b^{3}}$ theo luỹ thừa cơ số a.

Với b > 0 và

b^{\frac{2}{3}} = a

ta có:
•

b^{2} = b^{\frac{2}{3} \cdot 3} = {(b^{\frac{2}{3}})}^{3} = a^{3} .

•

\sqrt{a} \cdot b = a^{\frac{1}{2}} \cdot b^{\frac{2}{3} \cdot \frac{3}{2}} = a^{\frac{1}{2}} \cdot {(b^{\frac{2}{3}})}^{\frac{3}{2}}

= a^{\frac{1}{2}} \cdot a^{\frac{3}{2}} = a^{\frac{1}{2} + \frac{3}{2}} = a^{2} .

•

\frac{a^{6}}{b^{3}} = \frac{a^{6}}{b^{\frac{2}{3} \cdot \frac{9}{2}}} = \frac{a^{6}}{{(b^{\frac{2}{3}})}^{\frac{9}{2}}} = \frac{a^{6}}{a^{\frac{9}{2}}} = a^{6 - \frac{9}{2}} = a^{\frac{3}{2}} .

Câu 23:

Cho a > 0, a ≠ 1,

a^{\frac{1}{2}} = b .

Tính:
a) log_a b;

b) log_a (a³b²);

\log_{\sqrt{a}} (\frac{a}{b});

\log_{a b} (a \sqrt{b}) .

Giải mỗi phương trình sau:
a)

Với a > 0, a ≠ 1 và

a^{\frac{1}{2}} = b

nên b > 0. Ta có:
a)

\log_{a} b = \log_{a} a^{\frac{1}{2}} = \frac{1}{2} .

\log_{a} (a^{3} b^{2}) = \log_{a} [a^{3} . {(a^{\frac{1}{2}})}^{2}]

= \log_{a} (a^{3} . a) = \log_{a} a^{4} = 4.

\log_{\sqrt{a}} (\frac{a}{b}) = \log_{a^{\frac{1}{2}}} (\frac{a}{a^{\frac{1}{2}}})

= 2 \log_{a} a^{1 - \frac{1}{2}} = 2 \log_{a} a^{\frac{1}{2}} = 2 \cdot \frac{1}{2} = a .

\log_{a b} (a \sqrt{b}) = \log_{a \cdot a^{\frac{1}{2}}} (a \sqrt{a^{\frac{1}{2}}}) = \log_{a^{\frac{3}{2}}} (a . a^{\frac{1}{4}})

= \frac{2}{3} \log_{a} (a^{1 + \frac{1}{4}}) = \frac{2}{3} \log_{a} a^{\frac{5}{4}} = \frac{2}{3} . \frac{5}{4} = \frac{5}{6} .

Câu 24:

15/07/2024

0, 5^{2 x^{2} + x - 1} = \frac{1}{4};

2^{x^{2} - 6 x - \frac{5}{2}} = 16 \sqrt{2};

27^{x^{2} - 4 x + 4} = 9^{x^{2} - 4};

0, 05^{x - 3} = {(2 \sqrt{5})}^{x};

e) log₃ 3(x – 2) = –1;

g)log₅ (x² + 1) + log_0,2 (4 – 5x – x²) = 0.

Giải mỗi bất phương trình sau:
a) 2^{5x + 1} > 0,25;

a) $0, 5^{2 x^{2} + x - 1} = \frac{1}{4} \Leftrightarrow 0, 5^{2 x^{2} + x - 1} = 0, 5^{2}$

⇔ 2x² + x – 1 = 2

$\Leftrightarrow 2 x^{2} + x - 3 = 0 \Leftrightarrow [\begin{array}{l} x = - \frac{3}{2} \\ x = 1 \end{array} .$
Vậy phương trình có nghiệm $x \in \{- \frac{3}{2}; 1\} .$
b) $2^{x^{2} - 6 x - \frac{5}{2}} = 16 \sqrt{2}$
$\Leftrightarrow 2^{x^{2} - 6 x - \frac{5}{2}} = 2^{4} {.2}^{\frac{1}{2}}$
$\Leftrightarrow 2^{x^{2} - 6 x - \frac{5}{2}} = 2^{\frac{9}{2}}$
$\Leftrightarrow x^{2} - 6 x - \frac{5}{2} = \frac{9}{2}$
$\Leftrightarrow x^{2} - 6 x - 7 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 7 \end{array} .$
Vậy phương trình có nghiệm x ∈ {–1; 7}.
c) $27^{x^{2} - 4 x + 4} = 9^{x^{2} - 4}$
$\Leftrightarrow 3^{3 (x^{2} - 4 x + 4)} = 3^{2 (x^{2} - 4)}$
$\Leftrightarrow 3 (x^{2} - 4 x + 4) = 2 (x^{2} - 4)$
$\Leftrightarrow 3 x^{2} - 12 x + 12 = 2 x^{2} - 8$
$\Leftrightarrow x^{2} - 12 x + 20 = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 10 \end{array} .$
Vậy phương trình có nghiệm x ∈ {2; 10}.
d) $0, 05^{x - 3} = {(2 \sqrt{5})}^{x} \Leftrightarrow {(\frac{1}{20})}^{x - 3} = {(2 \sqrt{5})}^{x}$
$\Leftrightarrow {(\frac{1}{2 \sqrt{5}})}^{2 (x - 3)} = {(2 \sqrt{5})}^{x} \Leftrightarrow {(2 \sqrt{5})}^{- 2 (x - 3)} = {(2 \sqrt{5})}^{x}$
⇔ –2(x – 3) = x ⇔ –3x = –6 ⇔ x = 2.
Vậy phương trình có nghiệm x = 2.
e) log3 3(x – 2) = –1 ⇔ 3(x – 2) = 3–1
$\Leftrightarrow 3 (x - 2) = \frac{1}{3} \Leftrightarrow x - 2 = \frac{1}{9} \Leftrightarrow x = \frac{19}{9} .$
Vậy phương trình có nghiệm $x = \frac{19}{9} .$
g) Ta có: log5 (x2 + 1) + log0,2 (4 – 5x – x2) = 0
$\Leftrightarrow \log_{5} (x^{2} + 1) + \log_{5^{- 1}} (4 - 5 x - x^{2}) = 0$
⇔ log5 (x2 + 1) – log5 (4 – 5x – x2) = 0
⇔ log5 (x2 + 1) = log5 (4 – 5x – x2)
$\Leftrightarrow \{\begin{cases} x^{2} + 1 = 4 - 5 x - x^{2} \\ x^{2} + 1 > 0 \end{cases}$
$\Leftrightarrow x^{2} + 1 = 4 - 5 x - x^{2}$ (do x² + 1 > 0 ∀x ∈ ℝ)
$\Leftrightarrow 2 x^{2} + 5 x - 3 = 0$ $\Leftrightarrow [\begin{array}{l} x = - 3 \\ x = \frac{1}{2} \end{array} .$
Vậy phương trình có nghiệm $x \in \{- 3; \frac{1}{2}\} .$

Câu 25:

20/07/2024

{(\frac{4}{9})}^{x - 1} \leq {(\frac{3}{2})}^{x + 2};

\log_{16} (3 x + 4) < - \frac{1}{4};

d) log_0,2 (x² – 6x + 9) ≥ log_0,2 (x – 3).

2^{5 x + 1} > 0, 25 \Leftrightarrow 2^{5 x + 1} > 2^{- 2}

\Leftrightarrow 5 x + 1 > - 2 \Leftrightarrow x > - \frac{3}{5} .

Vậy bất phương trình có tập nghiệm là

(- \frac{3}{5}; + \infty) .

{(\frac{4}{9})}^{x - 1} \leq {(\frac{3}{2})}^{x + 2} \Leftrightarrow {(\frac{2}{3})}^{2 (x - 1)} \leq {(\frac{3}{2})}^{x + 2} \Leftrightarrow {(\frac{3}{2})}^{- 2 (x - 1)} \leq {(\frac{3}{2})}^{x + 2}

⇔ –2(x – 1) ≤ x + 2 (do

\frac{3}{2} > 1)

⇔ –3x ≤ 0 ⇔ x ≥ 0.
Vậy bất phương trình có tập nghiệm là (0; + ∞).
c) Ta có:

\log_{16} (3 x + 4) < - \frac{1}{4} \Leftrightarrow 0 < 3 x + 4 < 16^{- \frac{1}{4}}

\Leftrightarrow 0 < 3 x + 4 < \frac{1}{2} \Leftrightarrow \{\begin{cases} 3 x + 4 > 0 \\ 3 x + 4 < \frac{1}{2} \end{cases} \Leftrightarrow \{\begin{cases} x > - \frac{4}{3} \\ x < - \frac{7}{6} \end{cases} \Leftrightarrow - \frac{4}{3} < x < - \frac{7}{6} .

Vậy bất phương trình có tập nghiệm là

(- \frac{4}{3}; - \frac{7}{6}) .

d) Ta có: log0,2 (x2 – 6x + 9) ≥ log0,2 (x – 3)

\Leftrightarrow \{\begin{cases} x^{2} - 6 x + 9 \leq x - 3 \\ x^{2} - 6 x + 9 > 0 \end{cases}

(Vì 0 < 0,2 < 1)

\Leftrightarrow \{\begin{cases} x^{2} - 7 x + 12 \leq 0 \\ {(x - 3)}^{2} > 0 \end{cases} \Leftrightarrow \{\begin{cases} 3 \leq x \leq 4 \\ x \neq 3 \end{cases} \Leftrightarrow 3 < x \leq 4

Vậy bất phương trình có tập nghiệm là (3; 4].

Câu 26:

23/07/2024

Số lượng của một loài vi khuẩn sau x giờ được tính bởi công thức f(x) = Ae^rx, trong đó, A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0). Biết số vi khuẩn ban đầu là 1 000 con và sau 10 giờ tăng trưởng thành 5 000 con.

a) Tính tỉ lệ tăng trưởng của vi khuẩn.

b) Hỏi sau khoảng bao nhiêu giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu (làm tròn kết quả đến hàng đơn vị)?

Do số vi khuẩn ban đầu là 1 000 con nên ta có: A = 1 000.

a) Biết sau 10 giờ tăng trưởng thành 5 000 con nên f(x) = f(10) = 5 000.

Ta có: f(x) = Ae^rx suy ra: $r x = \ln (\frac{f (x)}{A})$

$\Rightarrow r = \frac{1}{x} . \ln (\frac{f (x)}{A}) = \frac{1}{10} \ln (\frac{5 000}{1 000}) = \frac{\ln 5}{10} .$

b) Khi số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu tức là f(x) = 10A nên ta có: $x = \frac{1}{r} . \ln (\frac{f (x)}{A}) = \frac{1}{r} \ln (\frac{10 A}{A}) = \frac{\ln 10}{r} .$

Thay  $r = \frac{\ln 5}{10}$   ta có  $x = \frac{\ln 10}{\frac{\ln 5}{10}} \approx 14.$

Vậy sau khoảng 14 giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu.

Câu 27:

11/07/2024

Với nước biển có nồng độ muối 30%, nhiệt độ T (^oC) của nước biển được tính bởi công thức T = 7,9ln(1,0245 – d) + 61,84, ở đó d (g/cm³) là khối lượng riêng của nước biển.

(Nguồn: Ron Larson, Intermediate Algebra, Cengage)

Biết vùng biển khơi mặt ở một khu vực có nồng độ muối 30% và nhiệt độ là 8 °C. Tính khối lượng riêng của nước biển ở vùng biển đó (làm tròn kết quả đến hàng phần chục nghìn).

Do vùng biển khơi mặt ở một khu vực có nồng độ muối 30% và nhiệt độ là 8 ^oC nên ta có T = 8. Suy ra: 7,9ln(1,0245 – d) + 61,84 = 8

$\Rightarrow \ln (1, 0245 - d) = - \frac{2 692}{395}$

$\Rightarrow 1, 0245 - d = e^{- \frac{2 692}{395}}$

$\Rightarrow d = 1, 0245 - e^{- \frac{2 692}{395}} \approx 1, 0234.$

Vậy khối lượng riêng của nước biển ở vùng biển đó là d ≈ 1,0234 (g/cm³).

Câu 28:

Cường độ của một trận động đất, kí hiệu là M (độ Richter), được cho bởi công thức M = logA – logA₀, ở đó A là biên độ rung chấn tối đa đo được bằng địa chấn kế và A₀ là biên độ chuẩn (hằng số phụ thuộc vào từng khu vực).

(Nguồn: https://vi.wikipedia.org/wiki/Độ_Richter)

Vào hồi 12 giờ 14 phút trưa ngày 27/07/2020, tại khu vực huyện Mộc Châu, Sơn La xảy ra trận động đất thứ nhất với cường độ 5,3 độ Richter. Trong vòng 20 tiếng đồng hồ, Sơn La đã xảy ra liên tiếp 7 trận động đất. Đến 8 giờ 26 phút sáng 28/07/2020, trận động đất thứ bảy xảy ra với cường độ 4 độ Richter.

Biết rằng biên độ chuẩn được dùng cho cả tỉnh Sơn La. Hỏi biên độ rung chấn tối đa của trận động đất thứ nhất gấp khoảng mấy lần biên độ rung chấn tối đa của trận động đất thứ bảy (làm tròn kết quả đến hàng đơn vị)?