Câu hỏi:
23/07/2024 140
Số lượng của một loài vi khuẩn sau x giờ được tính bởi công thức f(x) = Aerx, trong đó, A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0). Biết số vi khuẩn ban đầu là 1 000 con và sau 10 giờ tăng trưởng thành 5 000 con.
a) Tính tỉ lệ tăng trưởng của vi khuẩn.
b) Hỏi sau khoảng bao nhiêu giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu (làm tròn kết quả đến hàng đơn vị)?
Số lượng của một loài vi khuẩn sau x giờ được tính bởi công thức f(x) = Aerx, trong đó, A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0). Biết số vi khuẩn ban đầu là 1 000 con và sau 10 giờ tăng trưởng thành 5 000 con.
a) Tính tỉ lệ tăng trưởng của vi khuẩn.
b) Hỏi sau khoảng bao nhiêu giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu (làm tròn kết quả đến hàng đơn vị)?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Do số vi khuẩn ban đầu là 1 000 con nên ta có: A = 1 000.
a) Biết sau 10 giờ tăng trưởng thành 5 000 con nên f(x) = f(10) = 5 000.
Ta có: f(x) = Aerx suy ra:
b) Khi số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu tức là f(x) = 10A nên ta có:
Thay ta có
Vậy sau khoảng 14 giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu.
Do số vi khuẩn ban đầu là 1 000 con nên ta có: A = 1 000.
a) Biết sau 10 giờ tăng trưởng thành 5 000 con nên f(x) = f(10) = 5 000.
Ta có: f(x) = Aerx suy ra:
b) Khi số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu tức là f(x) = 10A nên ta có:
Thay ta có
Vậy sau khoảng 14 giờ thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng vi khuẩn ban đầu.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tập nghiệm của bất phương trình log2(3x – 1) < 3 là:
A. (– ∞; 3);
B.
C.
D.
Tập nghiệm của bất phương trình log2(3x – 1) < 3 là:
A. (– ∞; 3);
B.
C.
D.
Câu 4:
Cho a là số thực dương. Viết các biểu thức sau về lũy thừa cơ số a:
a)
b)
c)
d)
a)
c)
Câu 5:
Cho x, y là các số thực dương khác 1. Rút gọn các biểu thức sau:
a)
b)
a)
Câu 7:
Giải mỗi bất phương trình sau:
a) 25x + 1 > 0,25;
b)
c)
d) log0,2 (x2 – 6x + 9) ≥ log0,2 (x – 3).
a) 25x + 1 > 0,25;
c)
Câu 10:
Nghiệm của phương trình là:
A. x = 3;
B. x = 1;
C. x = – 3;
D. x = – 1.
Nghiệm của phương trình là:
A. x = 3;
B. x = 1;
C. x = – 3;
D. x = – 1.
Câu 12:
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = ax, y = bx, y = cx được cho bởi Hình 5. Kết luận nào sau đây là đúng đối với ba số a, b, c?
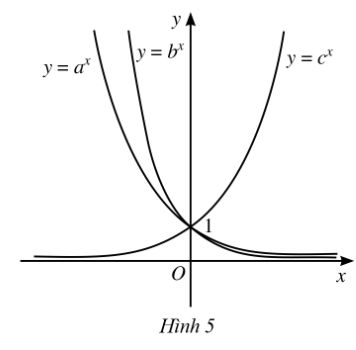
A. c < a < b;
B. c < b < a;
C. a < b < c;
D. b < a < c.
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = ax, y = bx, y = cx được cho bởi Hình 5. Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c < a < b;
B. c < b < a;
C. a < b < c;
D. b < a < c.
Câu 13:
Nghiệm của phương trình 3x – 1 = 1 là:
A. x = 1;
B. x = 0;
C. x = 2;
D. x = – 1.
Nghiệm của phương trình 3x – 1 = 1 là:
A. x = 1;
B. x = 0;
C. x = 2;
D. x = – 1.
Câu 15:
Nếu log2 = a thì log 4 000 bằng:
A. 2a + 3;
B. 3a2;
C.
D. a2 + 3.
Nếu log2 = a thì log 4 000 bằng:
A. 2a + 3;
B. 3a2;
C.
D. a2 + 3.


