Câu hỏi:
22/07/2024 106
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A.
B.
C. y = log0,3x;
D. y = –log2x.
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A.
B.
C. y = log0,3x;
D. y = –log2x.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
− Hàm số mũ đồng biến trên ℝ vì
− Ba hàm số còn lại nghịch biến trên tập xác định của chúng.
⦁ Hàm số mũ nghịch biến trên ℝ vì
⦁ Hàm số lôgarit y = log0,3x nghịch biến trên (0; +∞) vì 0 < 0,3 < 1.
⦁ Hàm số lôgarit nghịch biến trên (0; +∞) vì
Đáp án đúng là: B
− Hàm số mũ đồng biến trên ℝ vì
− Ba hàm số còn lại nghịch biến trên tập xác định của chúng.
⦁ Hàm số mũ nghịch biến trên ℝ vì
⦁ Hàm số lôgarit y = log0,3x nghịch biến trên (0; +∞) vì 0 < 0,3 < 1.
⦁ Hàm số lôgarit nghịch biến trên (0; +∞) vì
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tập nghiệm của bất phương trình log2(3x – 1) < 3 là:
A. (– ∞; 3);
B.
C.
D.
Tập nghiệm của bất phương trình log2(3x – 1) < 3 là:
A. (– ∞; 3);
B.
C.
D.
Câu 4:
Cho a là số thực dương. Viết các biểu thức sau về lũy thừa cơ số a:
a)
b)
c)
d)
a)
c)
Câu 5:
Cho x, y là các số thực dương khác 1. Rút gọn các biểu thức sau:
a)
b)
a)
Câu 9:
Nghiệm của phương trình là:
A. x = 3;
B. x = 1;
C. x = – 3;
D. x = – 1.
Nghiệm của phương trình là:
A. x = 3;
B. x = 1;
C. x = – 3;
D. x = – 1.
Câu 11:
Giải mỗi bất phương trình sau:
a) 25x + 1 > 0,25;
b)
c)
d) log0,2 (x2 – 6x + 9) ≥ log0,2 (x – 3).
a) 25x + 1 > 0,25;
c)
Câu 12:
Nghiệm của phương trình 3x – 1 = 1 là:
A. x = 1;
B. x = 0;
C. x = 2;
D. x = – 1.
Nghiệm của phương trình 3x – 1 = 1 là:
A. x = 1;
B. x = 0;
C. x = 2;
D. x = – 1.
Câu 13:
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = ax, y = bx, y = cx được cho bởi Hình 5. Kết luận nào sau đây là đúng đối với ba số a, b, c?
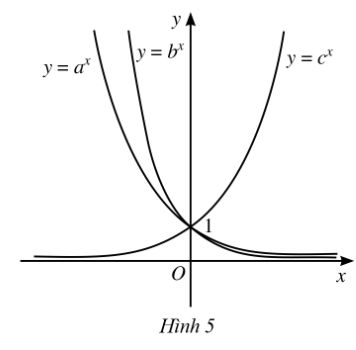
A. c < a < b;
B. c < b < a;
C. a < b < c;
D. b < a < c.
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = ax, y = bx, y = cx được cho bởi Hình 5. Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c < a < b;
B. c < b < a;
C. a < b < c;
D. b < a < c.
Câu 15:
Nếu log2 = a thì log 4 000 bằng:
A. 2a + 3;
B. 3a2;
C.
D. a2 + 3.
Nếu log2 = a thì log 4 000 bằng:
A. 2a + 3;
B. 3a2;
C.
D. a2 + 3.


