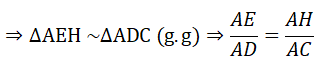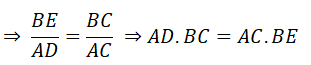Đề kiểm tra 1 tiết Toán 9 Chương 3 Hình học có đáp án
-
2614 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
19/07/2024Biết diện tích hình tròn là 64π () . Chu vi hình tròn này bằng:
Xem đáp án
Đáp án là B
S = π = 64π ⇒ R = 8
Chu vi hình tròn là: C = 2πR = 2π.8 = 16π cm
Câu 3:
19/07/2024Cho đường tròn O và góc nội tiếp ∠BAC = . Số đo độ của cung nhỏ BC bằng:
Xem đáp án
Đáp án là D
Câu 4:
19/07/2024Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.
Xem đáp án
Đáp án là C
Câu 5:
23/07/2024Cho tứ giác ABCD nội tiếp đường tròn (O). Hai cạnh đối AB và CD cắt nhau tại một điểm M ở ngoài (O), biết ∠BAD = thì góc BMC bằng:
Xem đáp án
Đáp án là A
Câu 7:
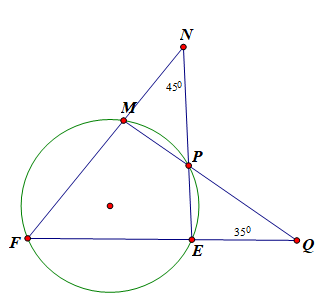
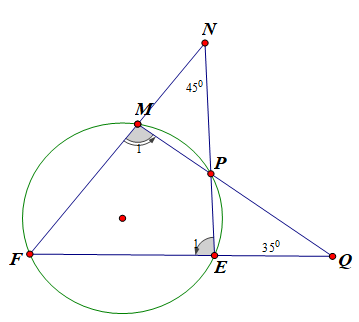
19/07/2024Cho hình vẽ, biết ∠(EQM) = ; ∠(FNE) = . Tính số đo ∠(NFQ)
Xem đáp án
Đáp án là A
Xét tam giác NEF có: ∠F + ∠N + ∠ = ⇒ ∠F + ∠E1 =
Xét tam giác FQM có: ∠F + ∠Q + ∠M1 = ⇒ ∠F + ∠M1 =
Do FMPE là tứ giác nội tiếp nên ∠E1 + ∠M1 =
Do đó ta có: 2∠F + = ⇒ ∠F =
Câu 9:
18/07/2024Phần tự luận
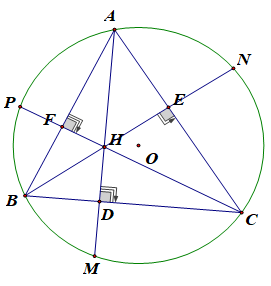
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
a) Tứ giác CEHD nội tiếp
Xem đáp án
a) Xét tứ giác CEHD có:
∠(CED) = (do BE là đường cao)
∠(HDC) = (do AD là đường cao)
⇒ ∠(CED) + ∠(HDC) =
Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp
Câu 10:
14/11/2024Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
b) Bốn điểm B, C, E, F cùng nằm trên một đường tròn
Xem đáp án
*Lời giải:
b) Xét tứ giác BFEC có:
∠(BFC) = (Do CF là đường cao)
∠(BEC ) = (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
*Phương pháp giải:
- Áp dụng các dấu hiệu nhận biết tứ giác nội tiếp đường tròn:
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp giải:Để chứng minh tứ giác nội tiếp ta có thể dùng một trong bốn dấu hiệu nhận biết tứ giác nội tiếp.
Cách 1: Chứng minh tứ giác có tổng hai góc đối bằng .
Cách 2: Chứng minh bốn đỉnh của tứ giác cùng các đều 1 điểm.
Cách 3: Chứng minh hai góc có đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh đó một góc không đổi.
Các 4: Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
* Lý thuyết cần nắm và các dạng bài tập về tứ giác nội tiếp/ ngoại tiếp đường tròn
- Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn.
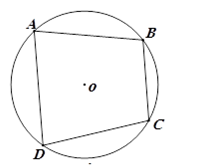
Trong hình vẽ trên, ta nói: Tứ giác ABCD nội tiếp đường tròn (O) và đường tròn (O) ngoại tiếp tứ giác ABCD.
Định lí
- Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng .
- Nếu một tứ giác có tổng số đo hai góc đối diện bằng thì tứ giác đó nội tiếp được đường tròn.
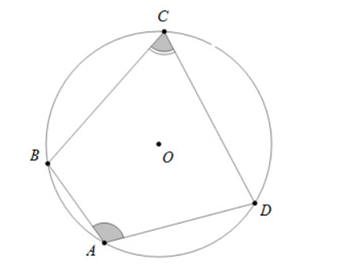
Xét hình vẽ:
- Tứ giác ABCD nội tiếp đường tròn (O) hoặc
- Tứ giác ABCD có hoặc thì tứ giác ABCD nội tiếp đường tròn.
Một số dấu hiệu nhận biết tứ giác nội tiếp
- Tứ giác có tổng các góc đối bằng là tứ giác nội tiếp.
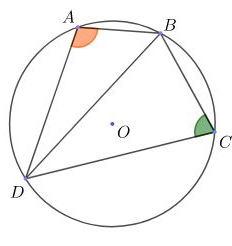
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay tứ giác ABCD là tứ giác nội tiếp.
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của một đỉnh đối diện là tứ giác nội tiếp.
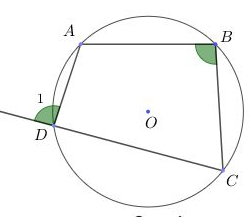
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay tứ giác ABCD là tứ giác nội tiếp.
- Tứ giác có bốn đỉnh cách đều một điểm cố định (mà ta xác định được) là tứ giác nội tiếp, điểm cách đều đó là tâm đường tròn nội tiếp tứ giác.
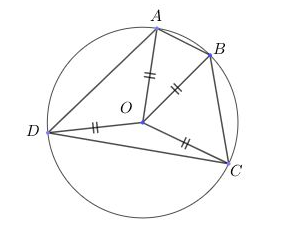
Xét hình vẽ:
Nếu OA = OB = OC = OD => Tứ giác ABCD nội tiếp đường tròn (O) hay tứ giác ABCD là tứ giác nội tiếp.
Điểm O chính là tâm đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc không đổi là tứ giác nội tiếp.
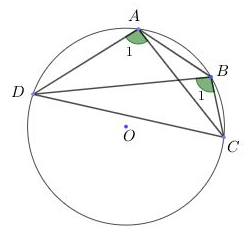
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay ABCD là tứ giác nội tiếp.
Dạng bài tập
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp giải:Để chứng minh tứ giác nội tiếp ta có thể dùng một trong bốn dấu hiệu nhận biết tứ giác nội tiếp.
Cách 1: Chứng minh tứ giác có tổng hai góc đối bằng .
Cách 2: Chứng minh bốn đỉnh của tứ giác cùng các đều 1 điểm.
Cách 3: Chứng minh hai góc có đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh đó một góc không đổi.
Các 4: Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Dạng 2: Chứng minh nhiều điểm thuộc cùng một đường tròn
Phương pháp giải: Ta chia các điểm đó thành các tứ giác, tam giác sau đó chứng minh cho các tứ giác, tam giác đó cùng nội tiếp một đường tròn.
Dạng 3: Sửng dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song, vuông góc…
Phương pháp giải:Sử dụng các tính chất của tứ giác nội tiếp.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp (mới 2024 + Bài Tập) - Toán 9
50 Bài tập Đường tròn ngoại tiếp, Đường tròn nội tiếp Toán 9 mới nhất
Câu 11:
20/07/2024Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
c) AE.AC = AH.AD ; AD.BC = BE.AC
Xem đáp án
c) Xét ΔAEH và ΔADC có:
∠(AEH) = ∠(ADC) =
∠(DAC) là góc chung
⇒ AE.AC = AD.AH
Xét Δ BEC và ΔADC có:
∠(BEC) = ∠(ADC) =
∠(ACD) là góc chung
⇒ ΔBEC ∼ ΔADC (g.g)
Câu 12:
02/11/2024Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
d) H và M đối xứng nhau qua BC
Xem đáp án
*Lời giải
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠() = ∠() ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠() = ∠()
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.
*Phương pháp giải
- vận dụng tính chất về góc nội tiếp chắc cung:
+ 2 góc nội tiếp chắn cùng 1 cung sẽ có số đo bằng nhau
*Lý thuyến cần nắm về đường tròn:
1. Định nghĩa góc nội tiếp
- Góc có đỉnh nằm trên đường tròn và hai cạnh là hai dây cung của đường tròn là góc nội tiếp.
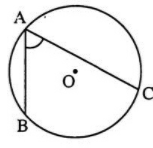
Góc có đỉnh A nằm trên đường tròn (O) và AB, AC là hai cạnh của góc cũng là hai dây của đường tròn. Do vậy là góc nội tiếp của đường tròn (O).
2. Định lý
- Trong một đường tròn, số đo góc nội tiếp bằng một nửa số đo cung bị chắn.
3. Hệ quả
Trong một đường tròn
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp (có số đo nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn nửa đường tròn là góc vuông.
Các dạng bài tập
Dạng 1: Chứng minh hai góc bằng nhau, đoạn thẳng bằng nhau, tam giác đồng dạng
Dùng hệ quả trong phần tóm tắt lí thuyết để chứng minh hai góc bằng nhau, hai đoạn thẳng bằng nhau.
Dạng 2: Chứng minh đường thẳng vuông góc, ba điểm thẳng hàng
Sử dụng các định lí, tính chất, hệ quả của góc ở tâm, góc nội tiếp.
Áp dụng quan hệ từ vuông góc đến song song, tiên đề Ơ clit.
Xem thêm các bài viết liên quan hay, chi tiết: