Câu hỏi:
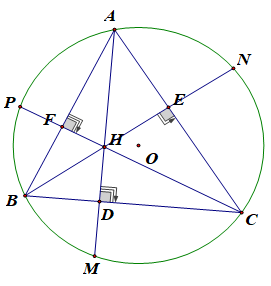
14/11/2024 177Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
b) Bốn điểm B, C, E, F cùng nằm trên một đường tròn
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
*Lời giải:
b) Xét tứ giác BFEC có:
∠(BFC) = (Do CF là đường cao)
∠(BEC ) = (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
*Phương pháp giải:
- Áp dụng các dấu hiệu nhận biết tứ giác nội tiếp đường tròn:
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp giải:Để chứng minh tứ giác nội tiếp ta có thể dùng một trong bốn dấu hiệu nhận biết tứ giác nội tiếp.
Cách 1: Chứng minh tứ giác có tổng hai góc đối bằng .
Cách 2: Chứng minh bốn đỉnh của tứ giác cùng các đều 1 điểm.
Cách 3: Chứng minh hai góc có đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh đó một góc không đổi.
Các 4: Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
* Lý thuyết cần nắm và các dạng bài tập về tứ giác nội tiếp/ ngoại tiếp đường tròn
- Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn.
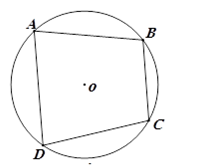
Trong hình vẽ trên, ta nói: Tứ giác ABCD nội tiếp đường tròn (O) và đường tròn (O) ngoại tiếp tứ giác ABCD.
Định lí
- Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng .
- Nếu một tứ giác có tổng số đo hai góc đối diện bằng thì tứ giác đó nội tiếp được đường tròn.
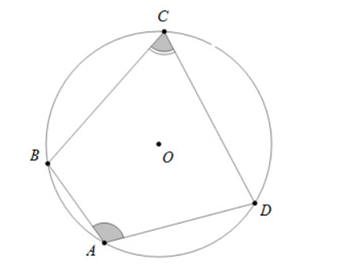
Xét hình vẽ:
- Tứ giác ABCD nội tiếp đường tròn (O) hoặc
- Tứ giác ABCD có hoặc thì tứ giác ABCD nội tiếp đường tròn.
Một số dấu hiệu nhận biết tứ giác nội tiếp
- Tứ giác có tổng các góc đối bằng là tứ giác nội tiếp.
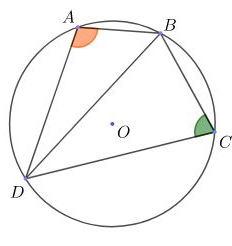
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay tứ giác ABCD là tứ giác nội tiếp.
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của một đỉnh đối diện là tứ giác nội tiếp.
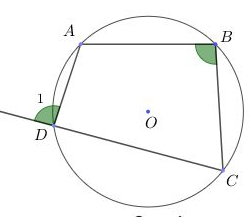
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay tứ giác ABCD là tứ giác nội tiếp.
- Tứ giác có bốn đỉnh cách đều một điểm cố định (mà ta xác định được) là tứ giác nội tiếp, điểm cách đều đó là tâm đường tròn nội tiếp tứ giác.
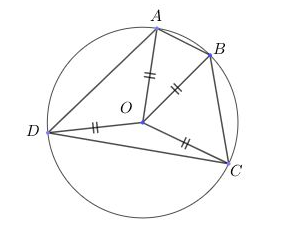
Xét hình vẽ:
Nếu OA = OB = OC = OD => Tứ giác ABCD nội tiếp đường tròn (O) hay tứ giác ABCD là tứ giác nội tiếp.
Điểm O chính là tâm đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc không đổi là tứ giác nội tiếp.
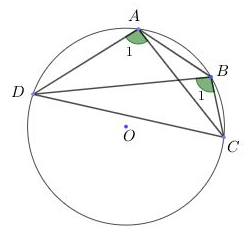
Xét hình vẽ:
Nếu => Tứ giác ABCD nội tiếp đường tròn hay ABCD là tứ giác nội tiếp.
Dạng bài tập
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp giải:Để chứng minh tứ giác nội tiếp ta có thể dùng một trong bốn dấu hiệu nhận biết tứ giác nội tiếp.
Cách 1: Chứng minh tứ giác có tổng hai góc đối bằng .
Cách 2: Chứng minh bốn đỉnh của tứ giác cùng các đều 1 điểm.
Cách 3: Chứng minh hai góc có đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh đó một góc không đổi.
Các 4: Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Dạng 2: Chứng minh nhiều điểm thuộc cùng một đường tròn
Phương pháp giải: Ta chia các điểm đó thành các tứ giác, tam giác sau đó chứng minh cho các tứ giác, tam giác đó cùng nội tiếp một đường tròn.
Dạng 3: Sửng dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song, vuông góc…
Phương pháp giải:Sử dụng các tính chất của tứ giác nội tiếp.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp (mới 2024 + Bài Tập) - Toán 9
50 Bài tập Đường tròn ngoại tiếp, Đường tròn nội tiếp Toán 9 mới nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
d) H và M đối xứng nhau qua BC
Câu 2:
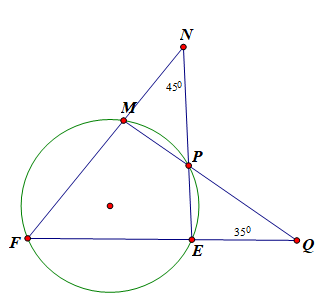
Cho đường tròn O và góc nội tiếp ∠BAC = . Số đo độ của cung nhỏ BC bằng:
Câu 3:
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Các tứ giác nào sau đây nội tiếp được đường tròn.
Câu 4:
Cho tứ giác ABCD nội tiếp đường tròn (O). Hai cạnh đối AB và CD cắt nhau tại một điểm M ở ngoài (O), biết ∠BAD = thì góc BMC bằng:
Câu 10:
Phần tự luận
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
a) Tứ giác CEHD nội tiếp
Câu 11:
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
c) AE.AC = AH.AD ; AD.BC = BE.AC