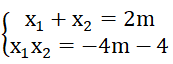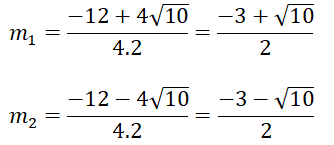Câu hỏi:
04/01/2025 633Cho phương trình (ẩn x) : x2 – 2mx – 4m – 4 = 0(1)
b) Tìm m để phương trình (1) có 2 nghiệm x1,x2 thỏa mãn x12+x22-x1x2=13 = 13
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
b) Gọi x1 ; x2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
x12+x22 -x1x2 = (x1+x2)2- 3x1 x2 = 4m2 + 3(4m + 4)
Theo bài ra: x12+x22 - x1 x2=13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ = 122 -4.4.(-1) = 160 ⇒
Phương trình có 2 nghiệm phân biệt
Vậy với 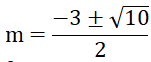
*Phương pháp giải:
Sử dụng viet tính x theo m
Sử dụng điều kiện để phương trình có 2 nghiệm
*Lý thuyết:
- Định lí Vi- ét:
+ Phương trình bậc hai có dạng () có hai nghiệm , , khi đó ta có:
+ Cho hai số u và v có tổng u + v = S và có tích u.v = P thì u và v là các nghiệm của phương trình:
- Định lí Vi-ét:
+) () có ()
+)
- Dấu của nghiệm phương trình bậc hai:
+) Hai nghiệm phân biệt cùng dấu
+) Hai nghiệm phân biệt dương
+) Hai nghiệm phân biệt âm
+) Hai nghiệm phân biệt trái dấu
Xem thêm
Bài tập về Hệ thức Vi-et và công thức Hệ thức Vi-et hay nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
Câu 2:
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
d) Tính theo R diện tích tam giác BDC.
Câu 3:
b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B
Câu 4:
Cho phương trình (ẩn x) : – 2mx – 4m – 4 = 0(1)
a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.
Câu 5:
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
Câu 6:
Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
Câu 7:
Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70.