Phần tự luận

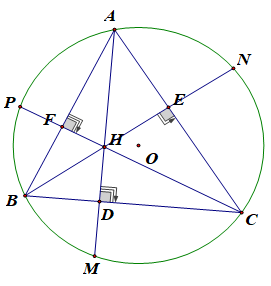
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

a) Tứ giác CEHD nội tiếp

Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

d) Tính theo R diện tích tam giác BDC.

Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.

Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.

Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC

Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70$m^2$.

Cho phương trình (ẩn x) : $x^2$ – 2mx – 4m – 4 = 0(1)

b) Tìm m để phương trình (1) có 2 nghiệm $x_1,x_2$ thỏa mãn ${x_1}^2+{x_2}^2-x_1{x}_2=13$ = 13

Cho phương trình (ẩn x) :$x^2$ – 2mx – 4m – 4 = 0(1)

a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.

b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B

a) Vẽ đồ thị (P) hàm số y= $x^2$/4

Giải các phương trình và hệ phương trình sau:

c) $\left\{\begin{array}{l}\sqrt{5}x-2y=7\\ x-\sqrt{5}y=2\sqrt{5}\end{array}\right.$