Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án
Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 2
-
1084 lượt thi
-
38 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 3:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Câu 4:
21/07/2024Cho hàm số y = f(x) có đồ thị như hình dưới đây.
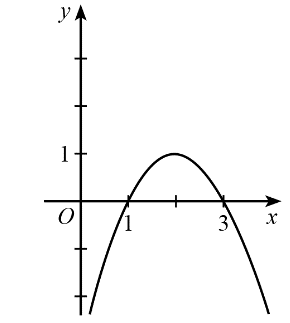
Trong các phát biểu sau, phát biểu nào sai?
 Xem đáp án
Xem đáp án
Đáp án: A
Câu 6:
08/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Lời giải
Bất phương trình ở đáp án Dcó dạng ax2 + bx + c ≥ 0 với a = 1, b = 2, c = -3
*Phương pháp giải:
SGK
*Lý thuyết:
Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng:
ax2 + bx + c ≤ 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c > 0, với a ≠ 0.
Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình ta được bất đẳng thức đúng.
Xem thêm
Lý thuyết Giải bất phương trình bậc hai một ẩn - Toán 10 Chân trời sáng tạo
Câu 8:
10/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 9:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: x2 – 8x + 7 ≥ 0 ⇔ [x≤1x≥7.
Suy ra tập nghiệm của bất phương trình là S = (– ∞; 1] ∪ [7; + ∞].
Do đó, [6; + ∞) ⊄ S.
Câu 10:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình – x2 + 2(m – 1)x + m – 3 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆' > 0
⇔ (m – 1)2 – (– 1) . (m – 3) > 0 ⇔ m2 – m – 2 > 0 ⇔[m<−1m>2.
Vậy m ∈ (– ∞; – 1) ∪ (2; + ∞).
Câu 11:
10/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình √−x2+4x=2x−2 ta được
– x2 + 4x = 4x2 – 8x + 4.
Sau khi thu gọn ta được 5x2 – 12x + 4 = 0. Từ đó tìm được x = 2 hoặc x=25.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 12:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cách 1. Thay lần lượt các giá trị ở từng đáp án vào cho đến khi tìm được giá trị thỏa mãn.
Cách 2. Giải phương trình
Bình phương hai vế của phương trình √3x2−6x+1=√x2−3 ta được
3x2 – 6x + 1 = x2 – 3.
Rút gọn ta được x2 – 3x + 2 = 0. Từ đó ta tìm được x = 1 hoặc x = 2.
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.
Vậy phương trình đã cho có 1 nghiệm là x = 2.
Câu 13:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
√−x2+4x−3=√2m+3x−x2⇔{−x2+4x−3≥0−x2+4x−3=2m+3x−x2⇔{1≤x≤3x=2m+3
Để phương trình (1) có nghiệm thì 1 ≤ 2m + 3 ≤ 3 ⇔ – 1 ≤ m ≤ 0 ⇒ m ∈ [– 1; 0].
Suy ra a = – 1, b = 0, do đó a2 + b2 = 1.
Câu 14:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 15:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 16:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 17:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai vectơ →a và →b cùng phương ⇔→a=k→b⇒{4=k(2m+6)−m=k⇒[m=−1m=−2.
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: →AB=(−2;−1),→AC=(4;−3).
Do đó, →AB⋅→AC=(−2)⋅4+(−1)⋅(−3)=−8+3=−5.
Câu 20:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Câu 21:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Câu 22:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Câu 23:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Cách 1. Thay tọa độ các điểm A, B lần lượt vào các phương trình trong các đáp án thì thấy đáp án B không thỏa mãn.
Cách 2. Nhận thấy rằng các phương trình ở các đáp án A, C, D thì vectơ chỉ phương của các đường thẳng đó cùng phương, riêng chủ có đáp án B thì không. Do đó chọn đáp án B.
Câu 25:
23/07/2024Câu 28:
16/07/2024 Xem đáp án
Xem đáp án
Câu 29:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính bằng nửa độ dài đoạn AB.
Ta có →AB=(4;−4), suy ra AB=√42+(−4)2=4√2.
Suy ra bán kính đường tròn là R=AB2=2√2.
Tọa độ tâm là {xI=1+52=3yI=3+(−1)2=1. Suy ra I(3; 1).
Phương trình đường tròn cần lập là: (x – 3)2 + (y – 1)2 = 8.
Câu 30:
12/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải
Ta có: 12 + 52 – 2 . 1 – 4 . 5 – 4 = 0, do đó A thuộc đường tròn (C).
Đường tròn (C) có tâm là I(1; 2). Tiếp tuyến của (C) tại A(1; 5) có vectơ pháp tuyến →AI=(0;−3), nên có phương trình
0(x – 1) – 3(y – 5) = 0 hay y – 5 = 0.
*Phương pháp giải:
- Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).
+ Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.
+ Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2
*Lý thuyết:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
- Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
- Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.
Xem thêm
Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)
Câu 31:
22/07/2024Trong mặt phẳng tọa độ Oxy, elip nào dưới đây có phương trình chính tắc dạng
x2a2+y2b2=1(a>b>0)?
 Xem đáp án
Xem đáp án
Đáp án: C
Câu 32:
21/07/2024 Xem đáp án
Xem đáp án
Câu 33:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Câu 34:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: 16x2 + 25y2 = 400 ⇔x225+y216=1.
Do đó, elip (E) có a = 5, b = 4, nên c = 3.
Vậy (E) có trục nhỏ bằng 2b = 8, có trục lớn bằng 2a = 10, có tiêu cự bằng 2c = 6 và có các tiêu điểm F1(– 3; 0) và F2(3; 0). Do đó, đáp án B sai.
Câu 35:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: a2 = 5 và b2 = 4 nên c2 = a2 + b2 = 9, suy ra c = 3.
Vậy tiêu cự của hypebol là 2c = 6.
Câu 36:
19/07/2024Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
 Xem đáp án
Xem đáp án
Đáp án:
a) Gọi đường thẳng cần lập là d.
Vectơ pháp tuyến của đường thẳng 3x + 5y – 2 = 0 cũng là một vectơ pháp tuyến của đường thẳng d nên phương trình đường thẳng d có dạng 3x + 5y + c = 0 (c ≠ – 2).
Vì d đi qua điểm M(– 1; – 4) nên 3 . (– 1) + 5 . (– 4) + c = 0. Suy ra c = 23 (t/m).
Vậy phương trình tổng quát của đường thẳng d là 3x + 5y + 23 = 0.
b) Gọi đường thẳng cần lập là a.
Đường thẳng a vuông góc với đường thẳng 2x + 3y + 7 nên lấy vectơ pháp tuyến →n=(2;3) của đường thẳng 2x + 3y + 7 là vectơ chỉ phương của đường thẳng a. Khi đó, một vectơ pháp tuyến của đường thẳng a là →na=(3;−2).
Đường thẳng a đi qua điểm N(1; 1) và có vectơ pháp tuyến là →na=(3;−2) nên có phương trình là 3(x – 1) – 2(y – 1) = 0 hay 3x – 2y – 1 = 0.
Câu 37:
21/07/2024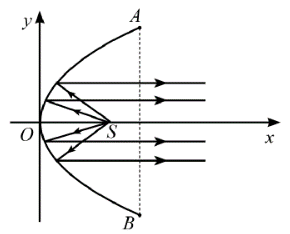
 Xem đáp án
Xem đáp án
Đáp án:
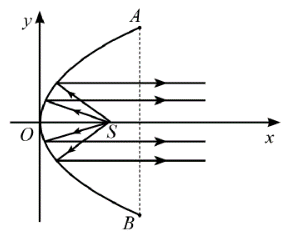
Parabol có phương trình chính tắc là: y2 = 2px (p > 0).
Vì AB = 40 cm và h = 30 cm nên A(30; 20).
Do A(30; 20) thuộc parabol nên ta có: 202 = 2p . 30 ⇒p=203.
Vậy parabol có phương trình chính tắc là: y2 = 403x.
Câu 38:
21/07/2024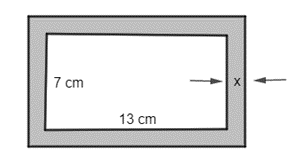
 Xem đáp án
Xem đáp án
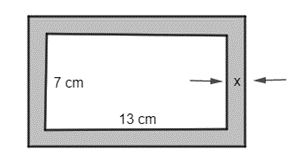
Diện tích hình chữ nhật bên trong khung ảnh (không bao gồm viền) là 7 . 13 = 91 (cm2).
Vì độ rộng viền xung quanh là x cm nên x > 0 và kích thước của khung ảnh là (7 + 2x) cm × (13 + 2x) cm.
Diện tích viền khung ảnh là: (7 + 2x)(13 + 2x) – 91 = 4x2 + 40x (cm2).
Theo bài ra ta có: 4x2 + 40x ≤ 44.
Giải bất phương trình trên ta được x ∈ [– 11; 1]. Do x > 0 nên x ∈ (0; 1].
Vậy độ rộng viền khung ảnh lớn nhất là 1 cm.
Bài thi liên quan
-
Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án - Đề 1
-
38 câu hỏi
-
60 phút
-
Có thể bạn quan tâm
- Đề kiểm tra giữa học kì 2 Toán 10 Chân trời sáng tạo có đáp án (1083 lượt thi)
Các bài thi hot trong chương
- Đề thi Học kì 1 Toán 10 Chân trời sáng tạo có đáp án (595 lượt thi)
- Đề thi Giữa kì 1 Toán 10 có đáp án (579 lượt thi)
