Đề kiểm tra 45 phút Toán 8 Chương 4 Đại Số có đáp án (Đề 5)
-
2160 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Đúng điền Đ, sai điền S vào các chỗ trống ở các khẳng định sau:
a)
Xem đáp án
a) S b) Đ
Câu 7:
18/07/2024Phần tự luận (7 điểm)
Chứng minh rằng nếu x > 0 và y > 0 thì
Xem đáp án
Ta có:
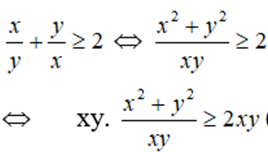
⇔ x2 + y2 ≥ 2xy ⇔ x2 – 2xy + y2 ≥ 0
⇔ (x – y)2 ≥ 0 (luôn đúng).
Câu 8:
19/07/2024Giải bất phương trình:
Xem đáp án
a) (x + 2)2 + 3(x + 1) ≥ x2 – 4
⇔ x2 + 4x + 4 + 3x + 3 ≥ x2 – 4
⇔ 7x + 7 ≥ –4
⇔ 7x ≥ –11
⇔ x ≥ -11/7
Tập nghiệm: S = {x|x ≥ -11/7}
b)
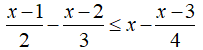
⇔ 6(x – 1) – 4(x – 2) ≤ 12x – 3(x – 3)
⇔ 6x – 6 – 4x + 8 ≤ 12x – 3x + 9
⇔ 2x + 2 ≤ 9x + 9
⇔ –7x ≤ 7 ⇔ x ≥ –1
Tập nghiệm: S = {x|x ≥ -1}
Câu 9:
22/07/2024Giải phương trình:
Xem đáp án
a) |2 – x| = |x – 5| ⇔ 2 – x = x – 5 hoặc 2 – x = –(x – 5)
⇔ 2x = 7 hoặc 2 – x = –x + 5 (vô nghiệm)
⇔ x = 7/2
Tập nghiệm: S = {7/2}
b) Điều kiện: x ≥ 0.
Khi đó: |2 – x| = x ⇔ 2 – x = x hoặc 2 – x = –x
⇔ x = 1
Tập nghiệm: S = {1}.
c) Ta có: |x| + |2 – x| ≥ |x + 2 – x| = 2
Dấu “=” xảy ra khi x và 2 – x cùng dấu.
- Nếu x ≥ 0 và 2 – x ≥ 0 ⇔ 0 ≤ x ≤ 2.
- Nếu x ≤ 0 và 2 – x ≤ 0 ⇔ x ≤ 0 và x ≥ 2 (vô nghiệm).
Vậy: 0 ≤ x ≤ 2.
Tập nghiệm: S = {x| 0 ≤ x ≤ 2}
Câu 10:
17/07/2024Cho a, b, c thỏa mãn: Chứng minh:
Xem đáp án
Ta có:
0 < a < 1 ⇒ a - 1 < 0 ⇒ a(a - 1) < 0 ⇒ a2 - a < 0 (1)
Tương tự:
0 < b < 1 ⇒ b2 - b < 0 (2)
0 < c < 1 ⇒ c2 - c < 0 (3)
Cộng (1); (2); (3) vế theo vế ta được:
a2 + b2 + c2 - a - b - c < 0
⇔ a2 + b2 + c2 < a + b + c
⇔ a2+ b2 + c2 < 2 (do a + b + c = 2)