Câu hỏi:
18/07/2024 246Phần tự luận (7 điểm)
Chứng minh rằng nếu x > 0 và y > 0 thì
xy+yx≥2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
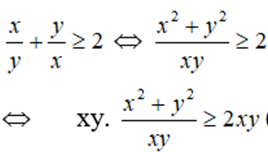
![]()
⇔ x2 + y2 ≥ 2xy ⇔ x2 – 2xy + y2 ≥ 0
⇔ (x – y)2 ≥ 0 (luôn đúng).