Đề kiểm tra 45 phút Toán 8 Chương 4 Đại Số có đáp án (Đề 3)
-
1901 lượt thi
-
9 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Đúng ghi Đ, sai ghi S vào ô trống. Cho a > b ta có:
Xem đáp án
a) S b) Đ c) S d) Đ
Câu 6:
22/07/2024Phần tự luận (7 điểm)
Chứng minh bất đẳng thức:
Xem đáp án
Ta có: a4 + 1 ≥ a(a2 + 1) ⇔ a4 + 1 ≥ a3 + a
⇔ a4 – a3 + 1 – a ≥ 0 ⇔ a3(a – 1) – (a – 1) ≥ 0
⇔ (a – 1)(a3 – 1) ≥ 0 ⇔ (a – 1)2(a2 + a + 1) ≥ 0
Ta thấy:
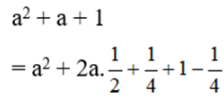
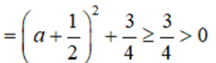
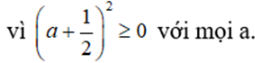
Vậy ≥ 0 với mọi a hay a4 + 1 ≥ a(a2 + 1)
Câu 7:
22/07/2024Giải bất phương trình:
Xem đáp án
a) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
b) (x – 3)2 + 4(2 – x) > x(x + 7)
⇔ x2 – 6x + 9 + 8 – 4x > x2 + 7x
⇔ –17x > –17
⇔ x < -17/-17
⇔ x < 1
Tập nghiệm: S = {x | x < 1}.
Câu 8:
22/07/2024Giải phương trình:
Xem đáp án
a) |x – 1| = |3 – 2x|
⇔ x – 1 = 3 – 2x hoặc x – 1 = –(3 – 2x)
⇔ 3x = 4 hoặc –x = –2
⇔ x = 4/3 hoặc x = 2
Tập nghiệm: S = {4/3; 2}
b) |–4x| + 3x = 1 ⇔ |4x| = 1 – 3x (*)
Điều kiện: 1 – 3x ≥ 0 ⇔ 1 ≥ 3x ⇔ (1/3) ≥ x hay x ≤ 1/3
Khi đó (*) ⇔ 4x = 1 – 3x hoặc 4x = –(1 – 3x)
⇔ 7x = 1 hoặc x = –1
⇔ x = 1/7 hoặc x = –1 (thỏa mãn điều kiện x ≤ 1/3 )
Tập nghiệm: S = {1/7; -1}
Câu 9:
22/07/2024a) Tìm x sao cho giá trị của biểu thức không lớn hơn giá trị của biểu thức
b) Cho hai số a, b > 0 và
Xem đáp án
a) x2 + 1 ≤ (x - 2)2 ⇔ x2 + 1 ≤ x2 - 4x + 4 ⇔ 4x ≤ 3
⇔ x ≤ 3/4
Vậy: x ≤ 3/4
b) a, b > 0
Ta có: a + b = 1 suy ra: (a + b)2 = 1 ⇒ a2 + 2ab + b2 = 1 (1)
Mặt khác (a - b)2 ≥ 0 với mọi a, b ⇒ a2 - 2ab + b2 ≥ 0 (2)
Cộng (1) và (2) vế theo vế, ta được:
2a2 + 2b2 ≥ 1 ⇒ 2(a2 + b2) ≥ 1 ⇒ a2 + b2 ≥ 1/2