Câu hỏi:
22/07/2024 154
Phần tự luận (7 điểm)
Chứng minh bất đẳng thức:
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: a4 + 1 ≥ a(a2 + 1) ⇔ a4 + 1 ≥ a3 + a
⇔ a4 – a3 + 1 – a ≥ 0 ⇔ a3(a – 1) – (a – 1) ≥ 0
⇔ (a – 1)(a3 – 1) ≥ 0 ⇔ (a – 1)2(a2 + a + 1) ≥ 0
Ta thấy:
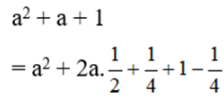
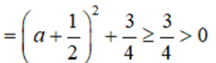
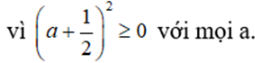
Vậy ≥ 0 với mọi a hay a4 + 1 ≥ a(a2 + 1)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
a) Tìm x sao cho giá trị của biểu thức không lớn hơn giá trị của biểu thức
b) Cho hai số a, b > 0 và
Xem đáp án »
22/07/2024
159











