30 câu hỏi trắc nghiệm thuộc 234 bài trắc nghiệm Hàm số và mũ Logarit từ đề thi Đại học cực hay có lời giải (P1) (Đề 4)

Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực R.

Xem đáp án

Câu 4:

Hàm số $y = a^{x} (0 < a < 1)$ có đồ thị (C). Mệnh đề nào sau đây sai?

A. Đồ thị (C) có tiệm cận y = 0.

B. Đồ thị (C) luôn nằm phía trên trục hoành

C. Đồ thị (C) luôn đi qua $M (0; 1)$ .

D. Hàm số luôn đồng biến trên R.

Xem đáp án

Chọn D

Câu 5:

Biết đồ thị hàm số $y = a^{x}$ và đồ thị hàm số $y = \log_{b} x$ cắt nhau tại điểm $A (\frac{1}{2}; 2)$ . Giá trị của biểu thức $T = a^{2} + 2 b^{2}$ bằng

Xem đáp án

Câu 6:

Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực R?

Xem đáp án

Câu 7:

14/07/2024

Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập R?

Xem đáp án

Câu 8:

Trong các hàm số sau, hàm số nào nghịch biến trên R?

Xem đáp án

Câu 9:

10/07/2024

Hàm số $y = {(0, 5)}^{x}$ có đồ thị là hình nào trong các hình sau đây?

Xem đáp án

Câu 10:

12/07/2024

Đồ thị sau là của hàm số nào?

Xem đáp án

Câu 11:

21/07/2024

Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

Xem đáp án

Câu 12:

18/07/2024

Trong các hàm số sau, hàm số nào nghịch biến?

Xem đáp án

Câu 13:

18/07/2024

Cho a > 1, chọn khẳng định đúng

B. Hàm số $y = \log_{a} x$ nghịch biến trên R

C. Hàm số $y = \log_{a} x$ đồng biến trên $(0; + \infty)$

D. Hàm số $y = \log_{a} x$ nghịch biến trên $(0; + \infty)$

Xem đáp án

Câu 14:

Cho hàm số $y = \log_{a} x$ $(0 < a \neq 1)$ có đồ thị là hình bên dưới. Giá trị của a bằng

Xem đáp án

Câu 15:

21/07/2024

Hàm số nào dưới đây đồng biến trên tập xác định của nó?

Xem đáp án

Câu 16:

Hàm số $y = \log_{3} (x^{2} - 2 x)$ nghịch biến trên khoảng nào?

Xem đáp án

Câu 17:

14/07/2024

Cho a,b,c dương và khác 1. Các hàm số $y = \log_{a} x, \log_{b} x, \log_{c} x$ có đồ thị như hình vẽ

Khẳng định nào dưới đây đúng?

Xem đáp án

Câu 18:

Hàm số $\log_{a} x$ và $\log_{b} x$ có đồ thị như hình vẽ dưới đây

Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ $x_{1}$ , $x_{2}$ . Biết rằng $x_{2} = 2 x_{1}$ , giá trị của $\frac{a}{b}$ bằng

Xem đáp án

Câu 19:

22/07/2024

Cho hàm số $y = \log_{a} x, y = \log_{b} x, y = \log_{c} x$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?

Xem đáp án

Câu 20:

Trong hình dưới đây, điểm B là trung điểm của đoạn thẳng AC. Khẳng định nào sau đây là đúng?

Xem đáp án

Câu 21:

Cho $y = e x + e^{- x}$ Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên R.

B. Hàm số nghịch biến trên R.

C. Hàm số đạt cực đại tại x = -1.

D. Hàm số đạt cực tiểu tại x = -1.

Xem đáp án

Câu 22:

16/07/2024

Trong y học các khối u ác tính được điều trị bằng xạ trị và hoá trị (sử dụng thuốc hoá học trị liệu). Xét một thí nghiệm y tế trong đó những con chuột có khối u ác tính được điều trị bằng một loại thuốc hoá học trị liệu. Tại thời điểm bắt đầu sử dụng thuốc khối u có thể tích khoảng $0, 5 c m^{3}$ , thể tích khối u sau t (ngày) điều trị xác định bởi công thức: $V (t) = 0, 005 e^{0, 24 t} + 0, 495 e^{- 0, 12 t}$ , $0 \leq t \leq 18 c m^{3}$ . Hỏi sau khoảng bao nhiêu ngày thì thể tích khối u là nhỏ nhất ?

A. 10,84 ngày

B. 9,87 ngày

C. 1,25 ngày

D. 8,13 ngày

Xem đáp án

Câu 23:

22/07/2024

Đồ thị hàm số nào dưới đây không có tiệm cận ngang?

Xem đáp án

Câu 24:

Điều kiện logarit | Lý thuyết, công thức, các dạng bài tập và cách giải

Hàm số $y = \log_{0, 5} (- x^{2} + 4 x)$ đồng biến trên khoảng

Xem đáp án

Câu 25:

06/12/2024

Tập hợp các số thực m để phương trình $\log_{2} x = m$ có nghiệm thực là

Xem đáp án

Đáp án đúng là D

Lời giải

*Phương pháp giải:

Xét hàm số $y = \log_{a} x$ , ta có 3 điều kiện hàm logarit ở dạng tổng quát như sau:

- $0 < a \neq 1$

- Xét trường hợp hàm số $y = \log_{a} [U (x)]$ điều kiện . Nếu $a$ chứa biến $x$ thì ta bổ sung điều kiện $0 < a \neq 1$

- Xét trường hợp đặc biệt: $y = \log_{a} {[U (x)]}^{n}$ điều kiện $U (x)$ >0 nếu n lẻ; $U (x) \neq 0$ nếu n chẵn.

*Lý thuyết:

1. Hàm số logarit

- Hàm số logarit cơ số $a$ là hàm số có dạng $y = \log_{a} x (0 < a \neq 1)$ .

- Hàm số logarit có đạo hàm tại $\forall x > 0$ và $y^{'} = {(\log_{a} x)}^{'} = \frac{1}{x \ln a}$

(đặc biệt ${(\ln x)}^{'} = \frac{1}{x}$ )

- Giới hạn liên quan $lim_{x \to 0} \frac{\ln (1 + x)}{x} = 1$ .

- Đạo hàm: $y = \log_{a} x \Rightarrow y^{'} = {(\log_{a} x)}^{'} = \frac{1}{x \ln a}; y = \log_{a} u (x) \Rightarrow y^{'} = \frac{u^{'} (x)}{u (x) \ln a}$

(đặc biệt ${(\ln x)}^{'} = \frac{1}{x}$ )

Khảo sát $y = \log_{a} x$ :

- TXĐ: $D = (0; + \infty)$

- Chiều biến thiên:

+ Nếu $a > 1$ thì hàm đồng biến trên $(0; + \infty)$ .

+ Nếu $0 < a < 1$ thì hàm nghịch biến trên $(0; + \infty)$ .

- Đồ thị:

+ Đồ thị hàm số có tiệm cận đứng $x = 0$ .

+ Đồ thị hàm số luôn đi qua các điểm $(1; 0)$ và $(a; 1)$ .

+ Đồ thị nằm hoàn toàn phía bên phải trục tung vì $x > 0$ .

+ Dáng đồ thị:

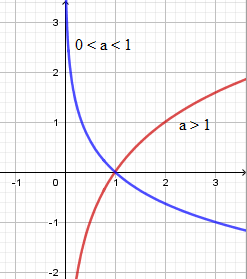
2. Điều kiện hàm logarit

Xét hàm số $y = \log_{a} x$ , ta có 3 điều kiện hàm logarit ở dạng tổng quát như sau:

- $0 < a \neq 1$

- Xét trường hợp hàm số $y = \log_{a} [U (x)]$ điều kiện . Nếu $a$ chứa biến $x$ thì ta bổ sung điều kiện $0 < a \neq 1$

- Xét trường hợp đặc biệt: $y = \log_{a} {[U (x)]}^{n}$ điều kiện $U (x)$ >0 nếu n lẻ; $U (x) \neq 0$ nếu n chẵn.

Tổng quát lại:

$y = \log_{a} u (x) (a > 0, a \neq 1)$

thì điều kiện xác định là $u (x) > 0$ và $u (x)$ xác định.

Xem thêm

TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12

Câu 26:

21/07/2024

Hàm số nào sau đây đồng biến trên $(- \infty; + \infty)$

Xem đáp án

Câu 27:

Cho hàm số y = f(x) liên tục và xác định trên R và có đồ thị như hình vẽ

Có bao nhiêu giá trị nguyên của m để bất phương trình

A. 5

B. Vô số.

C. 7

D. 6

Xem đáp án

Câu 28:

09/07/2024

Cho các hàm số $f_{0} (x), f_{1} (x), f_{2} (x), . . . .$ thỏa mãn:

$f_{0} (x) = \ln x + |\ln x - 2019|, f_{n + 1} (x) = |f_{n} (x)| - 1 \forall n \in N$ .Số nghiệm của phương trình $f_{2020} (x) = 0$ là

A. 6058.

B. 6057.

C. 6059.

D. 6063.

Xem đáp án

Câu 29: