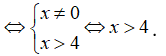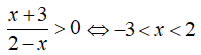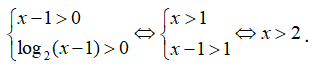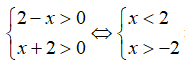174 Bài tập Hàm số mũ Logarit cực hay từ đề thi đại học có đáp án
174 Bài tập Hàm số mũ Logarit cực hay từ đề thi đại học có đáp án(P1) (Đề 3)
-
672 lượt thi
-
35 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Tìm tập xác định của hàm số y .
 Xem đáp án
Xem đáp án
Chọn D
Hàm số xác định khi và chỉ khi : ![]()
Câu 2:
14/07/2024Tìm tập xác định của hàm số .
 Xem đáp án
Xem đáp án
Chọn C
Xét hàm số
Điều kiện xác định của hàm số : ![]()
![]()
Tập xác định 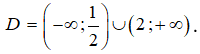
Câu 4:
14/07/2024Tập hợp các giá trị của x để biểu thức có nghĩa là
 Xem đáp án
Xem đáp án
Ta có ![]()
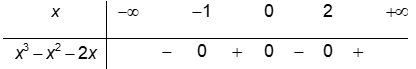
Vậy ![]() thì biểu thức có nghĩa.
thì biểu thức có nghĩa.
Chọn B
Câu 5:
13/11/2024Hàm số nào dưới đây đồng biến trên tập xác định của nó?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Ta có hàm số đồng biến trên khi a > 1 nên chọn đáp án B.
*Phương pháp giải:
- Dựa vào tính đơn điệu của hàm số mũ: Cho hàm số y = ax, (a > 0; a ≠ 1). Khi đó:
Nếu a > 1 thì hàm số đồng biến trên R
Nếu 0 < a < 1 thì hàm số nghịch biến trên R
*Các dạng bài tập thường gặp sự đồng biến/nghịch biến của hàm mũ:
* Phương pháp chung:
Bước 1: Tìm tập xác định D.
Bước 2: Tính đạo hàm y' = f'(x).
Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.
Bước 4: Lập bảng biến thiên.
Bước 5: Kết luận.
- Dựa vào tính đơn điệu của hàm số mũ:
Cho hàm số y = ax, (a > 0; a ≠ 1). Khi đó:
Nếu a > 1 thì hàm số đồng biến trên R
Nếu 0 < a < 1 thì hàm số nghịch biến trên R
* Dạng bài toán:
Dạng 1: Tìm giá trị của m để hàm số đơn điệu trên R.
* Phương pháp làm bài:
– Bước 1: Tính f′(x).
– Bước 2: Nêu các điều kiện của bài toán:
+ Hàm số y=f(x) đồng biến trên R⇔y′=f′(x)⩾0,với ∀x∈R và y′=0 tại một hữu hạn điểm.
+ Hàm số y=f(x) nghịch biến trên R⇔y′=f′(x)⩽0,với ∀x∈R và y′=0 tại một hữu hạn điểm.
– Bước 3: Từ các điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất và tam thức bậc hai để tìm m.
Dạng 2: Tìm m để hàm số đơn điệu trên miền D đã cho trước.
* Phương pháp làm bài:
– Bước 1: Nêu các điều kiện để hàm số đơn điệu trên D:
+ Hàm số y=f(x) đồng biến trên D⇔y′=f′(x)⩾0, với ∀x∈D.
+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)⩽0,với ∀x∈D.
– Bước 2: Từ điều kiện trên hãy sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.
- Bước 3: Kết luận
c) Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng
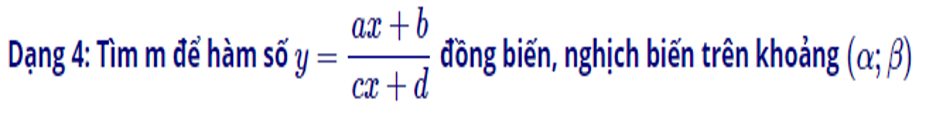
– Bước 1: Tính y′
– Bước 2: Nêu điều kiện để hàm số đồng biến và nghịch biến:
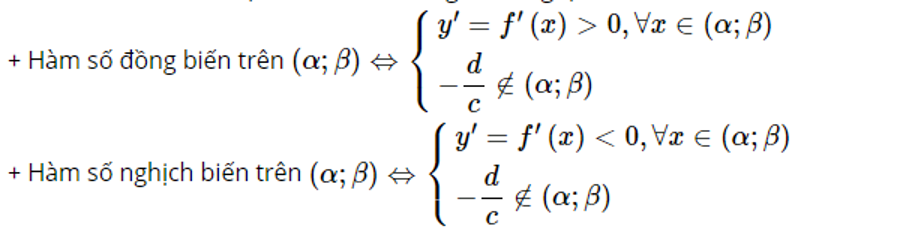
– Bước 3: Đưa ra kết luận.
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án)
Bài tập Sự đồng biến nghịch biến của hàm số Toán 12 mới nhất
Câu 6:
14/07/2024Tập xác định D của hàm số y = là
 Xem đáp án
Xem đáp án
Chọn D
Hàm số y = xác định khi ![]()
Vậy tập xác định ![]()
Câu 7:
15/07/2024Tìm tập xác định D của hàm số f(x) =
 Xem đáp án
Xem đáp án
Chọn D
Do không nguyên nên hàm số xác định khi và chỉ khi: ![]()
Vậy tập xác định của hàm số trên là ![]()
Câu 8:
20/07/2024Tập xác định của hàm số là?
 Xem đáp án
Xem đáp án
Chọn B
Hàm số xác định khi: 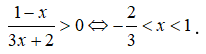
Vậy tập xác định của hàm số là: 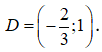
Câu 9:
16/07/2024Tìm tất cả các giá trị thực của tham số m để hàm số có tập xác định là .
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện xác định của hàm số trên ![]()
Để tập xác định của hàm số là thì 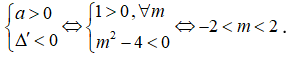
Vậy đáp án đúng là đáp án D.
Câu 14:
23/07/2024Hàm số có tập xác định là
 Xem đáp án
Xem đáp án
Chọn B
Hàm số xác định khi
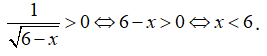
Vậy tập xác định của hàm số là ![]()
Câu 16:
20/07/2024Hàm số có tập xác định là D = khi
 Xem đáp án
Xem đáp án
Chọn C
Hàm số có tập xác định là D = ![]()
Đặt ![]() Khi đó, bất phương trình (1) trở thành:
Khi đó, bất phương trình (1) trở thành:
![]()
![]()
Xét hàm số ![]()
Ta có: f '(t) = -2t + 1; f '(t) = 0
Bảng biến thiên:
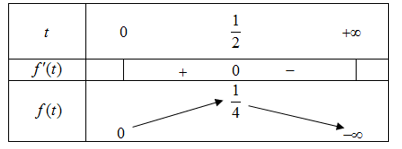
Dựa vào bảng biến thiên, suy ra 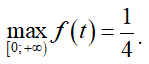
Từ (*) suy ra 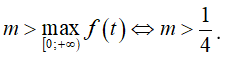
Câu 17:
13/07/2024Tìm tất cả các giá trị thực của tham số m để hàm số có tập xác định là .
 Xem đáp án
Xem đáp án
Chọn D
Hàm số có tập xác định là khi và chỉ khi
![]()
![]()
Câu 18:
13/07/2024Tập xác định của hàm số có chứa bao nhiêu số nguyên?
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện:
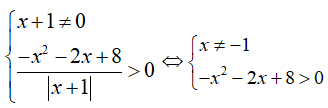
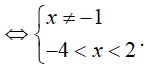
Vậy tập xác định của hàm số f(x) là ![]() suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1
suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1
Câu 19:
16/07/2024Tập xác định của hàm số là Giá trị của a bằng
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện xác định của hàm số đã cho là:
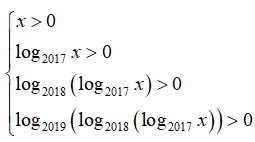
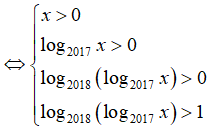
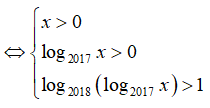
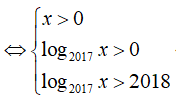
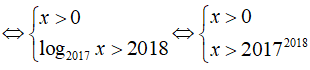
![]()
Câu 20:
13/07/2024Tìm tất cả các giá trị của tham số m để hàm số xác định trên khoảng
 Xem đáp án
Xem đáp án
Chọn A
Cách 1
Điều kiện: x > 0
Hàm số xác định khi:
![]()
![]()
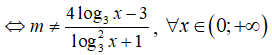
Để hàm số xác định trên thì phương trình 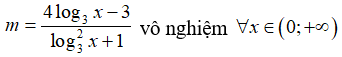
Xét hàm số 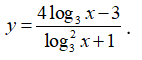
Đặt ![]() khi đó ta có
khi đó ta có
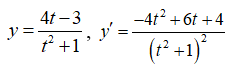
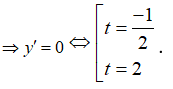
Ta có BBT:
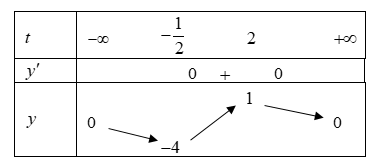
Để hàm số xác định trên ![]()
Cách 2:
Đề hàm số xác định trên khoảng ![]() thi phương trình
thi phương trình ![]() vô nghiệm.
vô nghiệm.
TH1: m = 0 thì PT trở thành ![]()
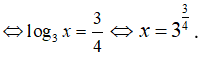
Vậy m = 0 không thỏa mãn.
TH2: 0 thì để PT vô nghiệm ![]()
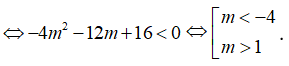
Để hàm số xác định trên ![]()
Câu 21:
14/07/2024Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện xác định:
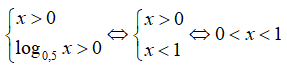
Từ đó suy ra tập xác định là D = (0;1)
Câu 22:
17/07/2024Bất phương trình có tập xác định D bằng
 Xem đáp án
Xem đáp án
Chọn B
Bất phương trình có điều kiện xác định:
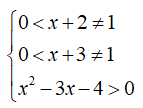
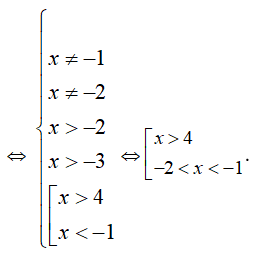
Vậy tập xác định của bất phương trình là ![]()
Câu 23:
20/07/2024Có bao nhiêu giá trị nguyên của tham số m trên [-2018;2018] để hàm số có tập xác định là ?
 Xem đáp án
Xem đáp án
Chọn C
Hàm số có tập xác định là khi và chỉ khi:
![]()
![]()
Câu 24:
13/07/2024Tìm tập xác định D của hàm số y = -log(2x-).
 Xem đáp án
Xem đáp án
Chọn B
Xét hàm số y = -log(2x-)
Điều kiện xác định 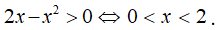
Tập xác định D = (0;2)
Câu 25:
14/07/2024Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019;2019) để hàm số sau có tập xác định là
 Xem đáp án
Xem đáp án
Chọn D
Hàm số xác định với mọi ![]() thì
thì 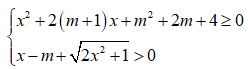 luôn đúng với mọi
luôn đúng với mọi ![]()
+) Ta có: ![]()
![]()
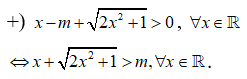
Xét hàm số ![]()
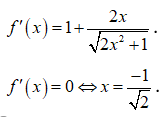
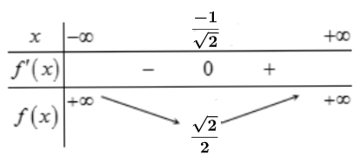
Từ bảng biến thiên ta thấy để 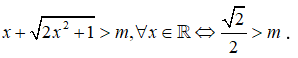
Kết hợp điều kiện
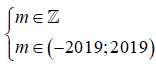
![]()
Kết luận: có 2019 giá trị của m thỏa mãn bài toán.
Câu 26:
22/07/2024Với giá trị nào của x thì biểu thức: f(x) = xác định?
 Xem đáp án
Xem đáp án
Chọn A
Biểu thức f(x) = xác định ![]()
![]()
![]()
Câu 27:
21/07/2024Cho hàm số y = với 0 < a 1. Mệnh đề nào sau đây SAI?
 Xem đáp án
Xem đáp án
Chọn D
Đồ thị hàm số y = với 0 < a 1. có tiệm cận ngang là trục hoành và không có tiệm cận đứng nên chọn D.
Câu 28:
17/07/2024Hàm số nào sau đây có đồ thị như hình bên?
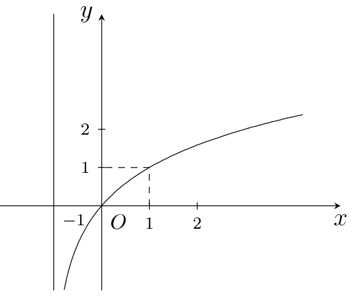
 Xem đáp án
Xem đáp án
Chọn C
Đồ thị hàm số đi qua điểm (0;0) nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm (1;1) nên loại D.
Vậy đáp án C thỏa mãn.
Câu 29:
21/07/2024Hàm số nào sau đây là hàm số mũ?
 Xem đáp án
Xem đáp án
Chọn B
Cho số thực dương a 1. Hàm số y = được gọi là hàm số mũ cơ số a.
Vậy đáp án đúng là .
Câu 30:
17/07/2024Đường cong ở hình vẽ dưới đây là đồ thị của hàm số nào dưới đây ?
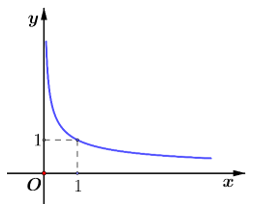
 Xem đáp án
Xem đáp án
Chọn B
Nhìn đồ thị ta thấy:
+ Tập xác định của hàm số: 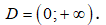
+ y' < 0 với mọi ![]()
+ Đồ thị đi qua điểm (1;1)
Vậy chỉ có hàm số ![]() thỏa mãn cả ba điều kiện trên.
thỏa mãn cả ba điều kiện trên.
Câu 31:
13/07/2024Cho dãy số thỏa mãn với mọi n1. Tìm số nguyên dương n > 1 nhỏ nhất để là một số nguyên.
 Xem đáp án
Xem đáp án
Chọn A
Với số tự nhiên n1, ta có:
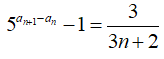
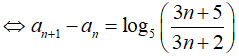
![]()
Suy ra:
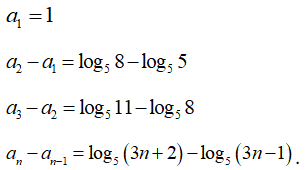
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n1
với mọi số tự nhiên n1
Để ![]()
![]()
Ta kiểm tra với các giá trị từ bé đến lớn
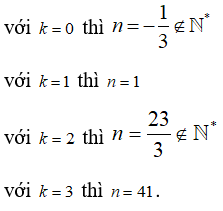
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
Câu 32:
14/07/2024Cho hàm số . Biết rằng ,f(2) + f(3) + ....+f(2020) = ln trong đó , là phân số tối giản, a, b. Tính b - 3a
 Xem đáp án
Xem đáp án
Chọn A
Ta có
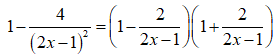
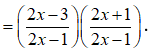

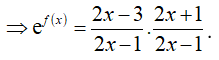
Vì f(2) + f(3) + ....+f(2020) = ln nên 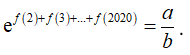
Mà ![]()
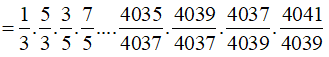
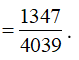
Do đó 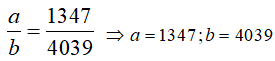
=> b - 3a = -2
Câu 33:
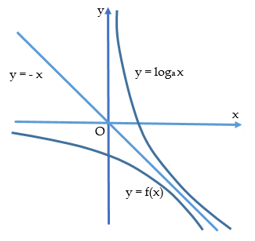
13/07/2024Biết đồ thị hàm số và y = f(x) đối xứng nhau qua đường thẳng y = f(x)(như hình vẽ). Giá trị là
 Xem đáp án
Xem đáp án
Chọn A
Gọi A(x;y) là điểm nằm trên đồ thị của hàm số , A(x',y') là điểm đối xứng với A qua đường thẳng y = -x,
ta có biểu thức tọa độ 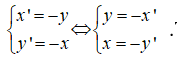
Thay vào hàm số ta được 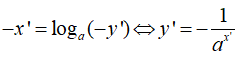
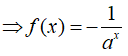
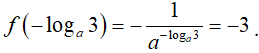
Vậy chọn A
Câu 34:
20/07/2024Trong hình dưới đây, điểm B là trung điểm của đoạn thẳng AC. Khẳng định nào sau đây là đúng?
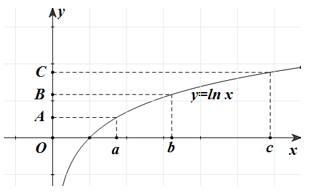
 Xem đáp án
Xem đáp án
Chọn B
Ta có ![]() và B là trung điểm của AC nên
và B là trung điểm của AC nên
![]()
![]()
Vậy ![]()
Câu 35:
20/07/2024Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số qua điểm I(2;1). Giá trị của biểu thức bằng
 Xem đáp án
Xem đáp án
Chọn D
Xét (); y = f(x) (C) và (C) đối xứng với () qua I(2;1).
Gọi điểm ![]() đối xứng với nhau qua điểm I(2;1), ta có:
đối xứng với nhau qua điểm I(2;1), ta có:
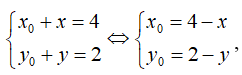
thay vào phương trình của () ta được:
![]()
![]()
Suy ra ![]() = -2017
= -2017
Như vậy, ![]()
Bài thi liên quan
-
174 Bài tập Hàm số mũ Logarit cực hay từ đề thi đại học có đáp án(P1) (Đề 1)
-
34 câu hỏi
-
50 phút
-
-
174 Bài tập Hàm số mũ Logarit cực hay từ đề thi đại học có đáp án(P1) (Đề 2)
-
35 câu hỏi
-
50 phút
-