Nội dung bài viết

    Xem thêm

    Giải bài tập trang 57, 58 Chuyên đề Toán 10 Bài 3 - Chân trời sáng tạo

    Với Giải bài tập trang 57, 58 Chuyên đề Toán 10 trong Bài 3: Parabol sách Chuyên đề Toán lớp 10 Chân trời sáng tạo  hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 57, 58.

    1 1,548 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập trang 57, 58 Chuyên đề Toán 10 Bài 3 - Chân trời sáng tạo

    Khám phá 1 trang 57 Chuyên đề Toán 10: Chứng tỏ rằng nếu điểm M(x0; y0) nằm trên parabol (P) thì điểm M'(x0; –y0) cũng nằm trên parabol (P).

    Lời giải:

    M(x0; y0) thuộc (P) thì y02=2px0.

    Có −y02=y02=2px0 nên M'(x0; –y0) cũng thuộc (P).

    Thực hành 1 trang 58 Chuyên đề Toán 10: Tìm toạ độ tiêu điểm, toạ độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:

    a) (P1): y2 = 2x;

    b) (P2): y2 = x;

    c) P3:y2=15x.

    Lời giải:

    a) Có 2p = 2, suy ra p = 1.

    Toạ độ tiêu điểm của parabol là F12;0.

    Toạ độ đỉnh của parabol là O(0; 0).

    Phương trình đường chuẩn của parabol là x = −12.

    Trục đối xứng của parabol là trục Ox.

    b) Có 2p = 1, suy ra p = 12.

    Toạ độ tiêu điểm của parabol là F14;0.

    Toạ độ đỉnh của parabol là O(0; 0).

    Phương trình đường chuẩn của parabol là x = -14

    Trục đối xứng của parabol là trục Ox.

    c) Có 2p = 15 suy ra p = 110

    Toạ độ tiêu điểm của parabol là F120;0.

    Toạ độ đỉnh của parabol là O(0; 0).

    Phương trình đường chuẩn của parabol là x = -120

    Trục đối xứng của parabol là trục Ox.

    Vận dụng 1 trang 58 Chuyên đề Toán 10: Trong mặt phẳng Oxy, cho điểm A(2; 0) và đường thẳng d: x + 2 = 0. Viết phương trình của đường (L) là tập hợp các tâm J(x; y) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.

    Lời giải:

    Có JA = 2−x2+0−y2=2−x2+y2.

    Khoảng cách từ J đến d là: d(J; d) = |x + 2|.

    Đường tròn (C) luôn đi qua A và tiếp xúc với d ⇔ JA = d(J; d)

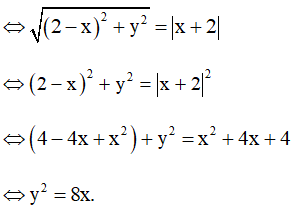
    Chuyên đề Toán 10 Bài 3: Parabol - Chân trời sáng tạo (ảnh 1)

    Vậy (L) là một parabol có phương trình y2 = 8x.

    Khám phá 2 trang 58 Chuyên đề Toán 10: Cho điểm M(x; y) trên parabol (P): y2 = 2px (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm F của (P).

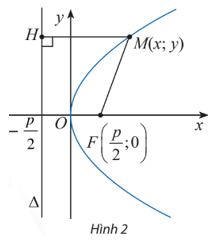
    Chuyên đề Toán 10 Bài 3: Parabol - Chân trời sáng tạo (ảnh 1)

    Lời giải:

    Vì M thuộc (P) nên y2 = 2px.

    Khoảng cách từ điểm M đến tiêu điểm F là: MF = x−p22+y−02

    =x2−px+p24+y2=x2−px+p24+2px=x2+px+p24

    =x+p22=x+p2=x+p2 (vì x + p2 > 0).

    Thực hành 2 trang 58 Chuyên đề Toán 10: Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng:

    a) Điểm M1(1; –4) trên (P1): y2 = 16x;

    b) Điểm M2(3; –3) trên (P2): y2 = 3x;

    c) Điểm M3(4; 1) trên P3: y2=14x.

    Lời giải:

    a) Có 2p = 16, suy ra p = 8.

    Bán kính qua tiêu của M1 là: 

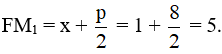
    Chuyên đề Toán 10 Bài 3: Parabol - Chân trời sáng tạo (ảnh 1)

    b) Có 2p = 3, suy ra p = 32

    Bán kính qua tiêu của M2 là:

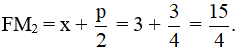
    Chuyên đề Toán 10 Bài 3: Parabol - Chân trời sáng tạo (ảnh 1)

    c) Có 2p = 14 suy ra p = 18

    Bán kính qua tiêu của M3 là:

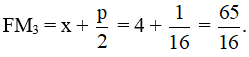
    Chuyên đề Toán 10 Bài 3: Parabol - Chân trời sáng tạo (ảnh 1)

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải bài tập trang 59 Chuyên đề Toán 10 Bài 3

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,548 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: