Nội dung bài viết

    Xem thêm

    Giải Bài tập trang 45, 46, 47 VTH Toán 7 Tập 1 - Kết nối tri thức

    Với Giải Bài tập trang 45, 46, 47 VTH Toán 7 Tập 1 trong Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 45, 46, 47.

    1 715 21/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Bài tập trang 45, 46, 47 VTH Toán 7 Tập 1 - Kết nối tri thức

    Bài 1 (3.17) trang 45 VTH Toán 7 Tập 1: Cho Hình 3.11, biết rằng mn // pq. Tính số đo các góc mHK, vHn.

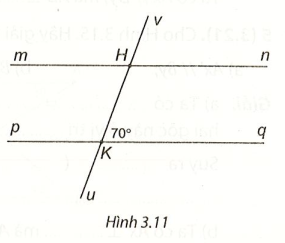
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    Ta có mn // pq

    Suy ra mHK^=HKq^=70° (hai góc so le trong)

    và vHn^=HKq^=70° (hai góc đồng vị)

    Bài 2 (3.18) trang 46 VTH Toán 7 Tập 1: Cho Hình 3.12.

    a) Giải thích tại sao Am // By.

    b) Tính CDm^.

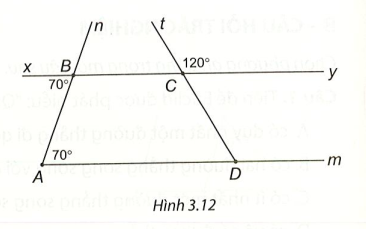
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    a) Ta có ABx^=BAD^=70°, mà hai góc này ở vị trí so le trong

    Suy ra Am // By (dấu hiệu nhận biết hai đường thẳng song song).

    b) Ta có Am // By, suy ra tCy^=CDm^=120° (hai góc đồng vị).

    Bài 3 (3.19) trang 46 VTH Toán 7 Tập 1: Cho Hình 3.13.

    a) Giải thích tại sao xx' // yy'

    b) Tính số đo góc MNB.

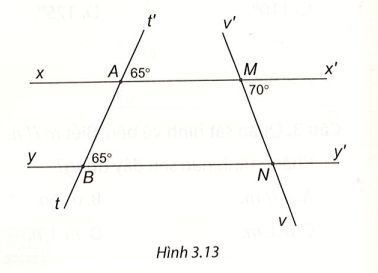
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    a) Ta có t' AM^=ABN^=65°.

    Mà hai góc này ở vị trí đồng vị

    Suy ra xx’ // yy’ (dấu hiệu nhận biết hai đường thẳng song song).

    b) Ta có xx’ // yy’ nên MNB^=NM^=70° (2 góc so le trong).

    Bài 4 (3.20) trang 46 VTH Toán 7 Tập 1: Cho Hình 3.14, biết rằng Ax // Dy, A^=90°,BCy^=50°. Tính số đo các góc ADC và ABC.

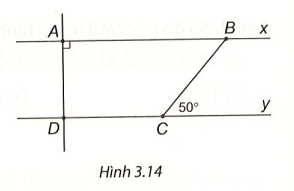
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    Ta có Ax // Dy, suy ra ABC^=yCB^=50° (hai góc so le trong)

    nên ABC^=50°

    Ta có Ax // Dy mà AD ⊥AB A^=90°, suy ra Dy ⊥ AD nên ADC^=90°

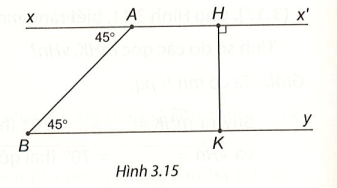
    Bài 5 (3.21) trang 46 VTH Toán 7 Tập 1: Cho Hình 3.15. Giải thích tại sao:

    a) Ax' // By

    b) By⊥HK.

    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    a) Ta có BAx^=ABy^=45°, mà hai góc này ở vị trí so le trong nên Ax // By hay Ax' // By (dấu hiệu nhận biết hai đường thẳng song song).

    b) Ta có HK⊥Ax' mà Ax' // By. Suy ra By⊥HK.

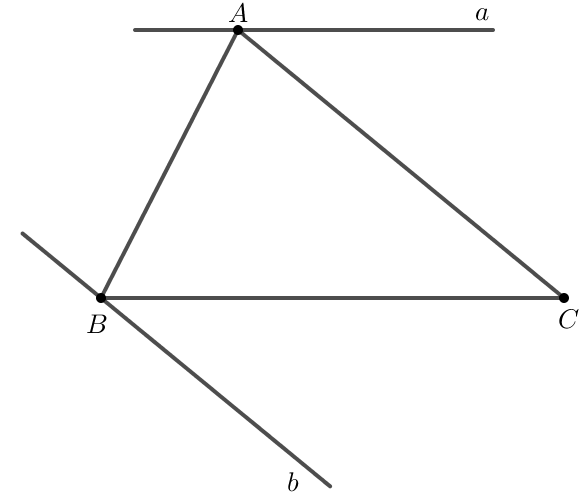
    Bài 6 (3.22) trang 47 VTH Toán 7 Tập 1: Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

    Lời giải:

    Theo tiên đề Euclid, chỉ vẽ được duy nhất một đường thẳng a, một đường thẳng b.

    Qua điểm A nằm ngoài đoạn BC, vẽ được duy nhất một đường thẳng song song với BC. Do đó ta chỉ có thể vẽ được 1 đường thẳng a.

    Qua điểm B nằm ngoài đoạn AC, vẽ được duy nhất một đường thẳng song song với AC. Do đó ta chỉ có thể vẽ được 1 đường thẳng b.

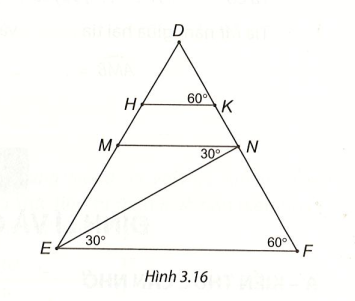
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Bài 7 (3.23) trang 47 VTH Toán 7 Tập 1: Cho Hình 3.16. Giải thích tại sao:

    a) MN // EF;

    b) HK // EF;

    c) HK // MN.

    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải:

    a) Ta có MNE^=NEF^=30°, mà hai góc này ở vị trí so le trong. Suy ra MN // EF (dấu hiệu nhận biết hai đường thẳng song song).

    b) Ta có DKH^=DFE^=60°, mà hai góc này ở vị trí đồng vị. Suy ra HK // EF (dấu hiệu nhận biết hai đường thẳng song song).

    c) Ta có HK // EF và MN // EF nên HK // MN.

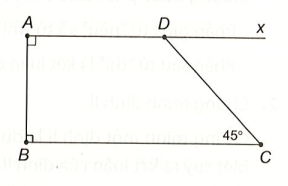
    Bài 8 trang 47 VTH Toán 7 Tập 1: Quan sát hình vẽ dưới đây tính CDx^.

    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải

    Ta có AD ⊥ AB và BC ⊥ AB nên AD // BC

    Suy ra CDx^=DCB^=45° (hai góc so le trong)

    Bài 9 trang 47 VTH Toán 7 Tập 1: Quan sát hình vẽ dưới đây và tính AMB^

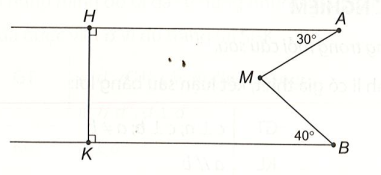
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Lời giải

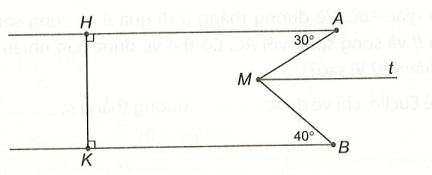
    Vở thực hành Toán 7 Bài 10: Tiên đề Euclid. Tính chất hai đường thẳng song song - Kết nối tri thức (ảnh 1)

    Ta có HA ⊥ HK và KB ⊥ HK  nên HA // KB

    Kẻ Mt // HA suy ra KB // Mt

    Ta có: AH // Mt, suy ra HAM^=AMt^=30° (hai góc so le trong)

    Ta có: BK // Mt, suy ra KBM^=BMt^=40° (hai góc so le trong)

    Tia Mt nằm giữa hai tia MA và MB nên AMB^=AMt^+BMt^=30°+40°=70°.

    Xem thêm lời giải Vở thực hành Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Câu hỏi trắc nghiệm trang 45 VTH Toán 7 Tập 1

     

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 715 21/08/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: