Chuyên đề Tin học 12 Bài 1 (Cánh diều): Đồ thị, phân loại đồ thị

Giải Chuyên đề Tin học 12 Bài 1: Đồ thị, phân loại đồ thị

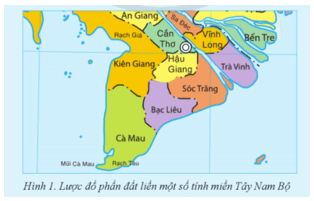
Khởi động trang 53 Chuyên đề Tin học 12: Để mô tả các cặp tỉnh có địa giới giáp ranh nhau, ta có thể nêu bằng lời, ví dụ, quan sát lược đồ bốn tỉnh Bạc Liêu, Cà Mau, Sóc Trăng và Kiên Giang trong Hình 1, ta nói "Các cặp tỉnh: (Bạc Liêu, Cà Mau), (Bạc Liêu, Sóc Trăng), (Bạc Liêu, Kiên Giang), (Kiên Giang, Cà Mau) giáp ranh nhau; còn (Kiên Giang, Sóc Trăng) và (Sóc Trăng, Cà Mau) không giáp ranh nhau". Em có cách mô tả nào khác về mối quan hê giáp ranh giữa các tỉnh đó không?

Lời giải:

Để mô tả các cặp tỉnh có địa giới giáp ranh nhau, ta có thể nêu bằng lời, ví dụ, quan sát lược đồ bốn tỉnh Bạc Liêu, Cà Mau, Sóc Trăng và Kiên Giang trong Hình 1, ta nói "Các cặp tỉnh: (Bạc Liêu, Cà Mau), (Bạc Liêu, Sóc Trăng), (Bạc Liêu, Kiên Giang), (Kiên Giang, Cà Mau) giáp ranh nhau; còn (Kiên Giang, Sóc Trăng) và (Sóc Trăng, Cà Mau) không giáp ranh nhau". Em mô tả nào khác về mối quan hê giáp ranh giữa các tỉnh đó như sau:

Bạc Liêu ---- Cà Mau

| |

| |

Sóc Trăng ---- Kiên Giang

Trong biểu đồ này, mỗi đường nối giữa hai điểm biểu thị rằng hai tỉnh đó giáp ranh nhau. Như vậy, ta có thể thấy rằng Bạc Liêu giáp ranh với Cà Mau, Sóc Trăng, và Kiên Giang; Cà Mau giáp ranh với Bạc Liêu và Kiên Giang; Sóc Trăng giáp ranh với Bạc Liêu; và Kiên Giang giáp ranh với Bạc Liêu và Cà Mau. Còn Sóc Trăng và Cà Mau không có đường nối, cho thấy hai tỉnh này không giáp ranh nhau. Tương tự, Kiên Giang và Sóc Trăng cũng không giáp ranh nhau.

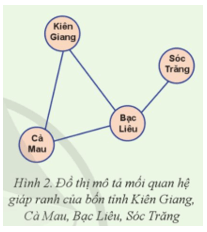
Hoạt động 1 trang 54 Chuyên đề Tin học 12: Việc mô tả mối quan hệ giáp ranh của bốn tỉnh Kiên Giang, Cà Mau, Bạc Liêu, Sóc Trăng trong phần khởi động có thể biểu diễn bằng bốn đỉnh (tương ứng với bốn vòng tròn nét liền) và bốn cạnh (tương ứng với bốn đường nối giữa hai vòng tròn cho biết cặp tỉnh giáp ranh) như trong Hình 2.

Em hãy vẽ Hình 2 vào vở và vẽ thêm hai vòng tròn mô tả hai tỉnh Cần Thơ, Hậu Giang cùng với các cạnh để mô tả mối quan hệ giáp ranh của sáu tỉnh.

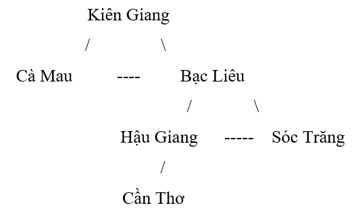
Lời giải:

- Hậu Giang giáp với: Bạc Liêu, Sóc Trăng, Kiên Giang.

- Cần Thơ giáp với: Kiên Giang, Hậu Giang

Câu 1 trang 56 Chuyên đề Tin học 12: Em hãy nêu ví dụ thực tế có thể sử dụng mô hình đồ thị để mô tả.

Lời giải:

Ví dụ về Mạng xã hội: Trong mạng xã hội, mỗi người dùng là một đỉnh và mối quan hệ bạn bè hoặc theo dõi là các cạnh. Điều này giúp phân tích mạng lưới xã hội và tìm ra các mối quan hệ quan trọng.

Ví dụ về Mối quan hệ dinh dưỡng giữa các loài: Chuột là thức ăn của Rắn nhưng Rắn không phải là thức ăn của Chuột, Rắn là thức ăn của Diều hâu.

Câu 2 trang 56 Chuyên đề Tin học 12: Xét đơn đồ thị có hướng gồm 6 đỉnh, các đỉnh được đánh chỉ số tương ứng từ 0 đến 5 từ 0 đến 5.

a) Em hãy xây dựng đồ thị, biết rằng với hai đỉnh được đánh chỉ số u, v (0 ≤ u, v ≤ 5), nếu u > v và u - v là một số nguyên tố thì đỉnh có chỉ số u có cạnh tới được đỉnh có chỉ số v.

b) Xác định bậc ra, bậc vào của từng đỉnh.

Lời giải:

Xét đơn đồ thị có hướng gồm 6 đỉnh, các đỉnh được đánh chỉ số tương ứng từ 0 đến 5:

Xác định các số nguyên tố từ 1 đến 5 (vì u và v có giá trị từ 0 đến 5 và u > v). Các số nguyên tố trong khoảng này là 2, 3 và 5. Vậy, chúng ta sẽ có một cạnh từ đỉnh u đến đỉnh v nếu u - v bằng một trong những số nguyên tố này.

a) Xây dựng đồ thị:

- Đỉnh 1 không có cạnh tới bất kỳ đỉnh nào khác vì không có số nguyên tố nào khi trừ đi 1.

- Đỉnh 2 sẽ có một cạnh tới đỉnh 0 (2 - 0 = 2).

- Đỉnh 3 sẽ có cạnh tới đỉnh 0 (3 - 0 = 3).

- Đỉnh 4 sẽ có cạnh tới đỉnh 1 và 3 (4 - 1 = 3 và 4 - 3 = 1, nhưng 1 không phải là số nguyên tố).

- Đỉnh 5 sẽ có cạnh tới đỉnh 0, 2 và 3 (5 - 0 = 5, 5 - 2 = 3 và 5 - 3 = 2).

Dựa vào cách xây dựng trên, ta có thể vẽ đồ thị như sau:

0 ← 2 ← 4

↓ ↓

1 3 ← 5

b) Xác định bậc ra và bậc vào của từng đỉnh:

- Đỉnh 0: Bậc vào = 3 (từ đỉnh 2, 3, 5), Bậc ra = 0.

- Đỉnh 1: Bậc vào = 1 (từ đỉnh 4), Bậc ra = 0.

- Đỉnh 2: Bậc vào = 1 (từ đỉnh 5), Bậc ra = 1 (tới đỉnh 0).

- Đỉnh 3: Bậc vào = 2 (từ đỉnh 4, 5), Bậc ra = 0.

- Đỉnh 4: Bậc vào = 0, Bậc ra = 2 (tới đỉnh 1 và 3).

- Đỉnh 5: Bậc vào = 0, Bậc ra = 3 (tới đỉnh 0, 2 và 3).

Vận dụng trang 56 Chuyên đề Tin học 12: Em hãy chọn ra 6 quận/huyện trong tỉnh/thành phố nơi em ở và xây dựng đồ thị vô hướng thể hiện mối quan hệ giáp ranh của các quận/huyện đó.

Lời giải:

Các quận/huyện được chọn là:

1. Quận Ba Đình

2. Quận Hoàn Kiếm

3. Quận Đống Đa

4. Quận Hai Bà Trưng

5. Quận Thanh Xuân

6. Quận Cầu Giấy

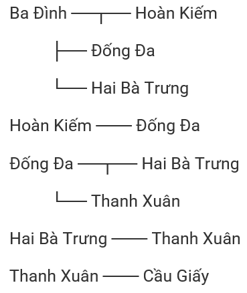
Theo thông tin giáp ranh, đồ thị vô hướng được xây dựng như sau:

Mỗi quận/huyện được biểu diễn bằng một đỉnh, và một đường nối giữa hai đỉnh biểu thị cho việc hai quận/huyện đó giáp ranh với nhau

Câu hỏi tự kiểm tra trang 56 Chuyên đề Tin học 12: Trong các câu sau đây, những câu nào đúng khi nói về đồ thị?

a) Trong đồ thị, mỗi cạnh thể hiện mối quan hệ giữa hai đối tượng (hai đỉnh).

b) Bậc của một đỉnh trong đơn đồ thị vô hướng có thể lẻ

c) Trong đồ thị có hướng tổng bậc ra của tất cả các đỉnh bằng tổng bậc vào của tất cả các đỉnh.

d) Tuỳ theo mối quan hệ của hai đỉnh u, v bất kì mà cạnh nối hai đỉnh đó có thứ tự hay không và tương ứng là đồ thị có hướng hay đồ thị vô hướng.

Lời giải:

a) Đúng. Vì đây là định nghĩa cơ bản của một đồ thị. Trong đồ thị, mỗi cạnh đại diện cho mối liên hệ giữa hai đối tượng (hai đỉnh) được kết nối với nhau.

b) Sai. Vì bậc của một đỉnh trong đơn đồ thị vô hướng luôn là số chẵn. Lý do là vì mỗi cạnh trong đồ thị vô hướng được xem như hai nửa cạnh có hướng ngược nhau. Do đó, khi đếm bậc của một đỉnh, mỗi cạnh sẽ được tính hai lần, dẫn đến kết quả là số chẵn.

c) Đúng. Vì trong đồ thị có hướng, mỗi cạnh xuất phát từ một đỉnh và đi vào một đỉnh khác. Do đó, tổng số bậc ra của tất cả các đỉnh bằng tổng số bậc vào của tất cả các đỉnh. Điều này thể hiện định luật bảo toàn bậc trong đồ thị có hướng.

d) Đúng. Vì đồ thị vô hướng: Hai đỉnh u và v được kết nối với nhau bởi một cạnh, và thứ tự kết nối hai đỉnh không quan trọng. Do đó, đồ thị vô hướng không phân biệt hướng của cạnh. Đồ thị có hướng: Cạnh nối hai đỉnh u và v được ký hiệu là (u, v), thể hiện mối quan hệ có hướng từ u sang v. Thứ tự kết nối hai đỉnh có quan trọng, và đồ thị có hướng phân biệt hướng của cạnh.

Vậy các câu đúng là: a,c,d.