Chuyên đề Tin học 12 Bài 5 (Cánh diều): Mô tả đặc trưng độ tập trung dữ liệu

Giải Chuyên đề Tin học 12 Bài 5: Mô tả đặc trưng độ tập trung dữ liệu

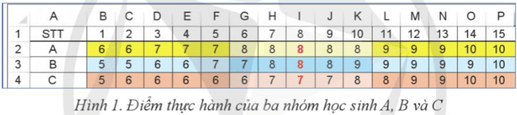
Khởi động trang 76 Chuyên đề Tin học 12: Bảng tính ở Hình 1 ghi lại điểm một bài thực hành môn Tin học được sắp xếp tăng dần của ba nhóm học sinh A, B và C. Coi mỗi dãy điểm là một mẫu số liệu. Theo em, trong ba tham số: trung bình, trung vị và mốt, tham số nào đặc trưng tốt cho từng mẫu số liệu?

Lời giải:

Bảng tính ở Hình 1 ghi lại điểm một bài thực hành môn Tin học được sắp xếp tăng dần của ba nhóm học sinh A, B và C. Coi mỗi dãy điểm là một mẫu số liệu.Theo em, trong ba tham số: trung bình, trung vị và mốt, tham số nào đặc trưng tốt cho từng mẫu số liệu như sau:

- Nhóm A:

Trung bình: Có thể không phản ánh chính xác do sự phân bố đều của dữ liệu.

Trung vị: Là 8, phản ánh tốt sự phân bố dữ liệu vì nó nằm ở giữa của dãy điểm.

Mốt: Là 8, phản ánh tốt vì nó xuất hiện nhiều lần, phản ánh điểm số phổ biến.

- Nhóm B:

Trung bình: Có thể cao hơn trung vị do sự tập trung điểm số cao ở cuối dãy.

Trung vị: Là 8, nhưng không đặc trưng tốt vì điểm số phổ biến hơn là 9.

Mốt: Là 9, đặc trưng tốt nhất vì nó phản ánh điểm số xuất hiện nhiều nhất.

- Nhóm C:

Trung bình: Có thể rất cao do nhiều điểm số 10.

Trung vị: Là 9, nhưng không phản ánh chính xác sự tập trung điểm số ở mức cao nhất.

Mốt: Là 10, phản ánh chính xác nhất vì nó là điểm số xuất hiện nhiều nhất và cao nhất trong nhóm.

- Trung bình và trung vị có thể không phản ánh chính xác sự phân bố điểm số nếu có sự tập trung điểm số ở một mức nhất định. Điều này đặc biệt rõ ràng ở nhóm C, nơi mà mốt là 10, phản ánh sự tập trung điểm số cao nhất trong nhóm. Mốt là tham số đặc trưng tốt nhất cho cả ba nhóm học sinh vì nó phản ánh điểm số xuất hiện nhiều nhất trong mỗi nhóm.

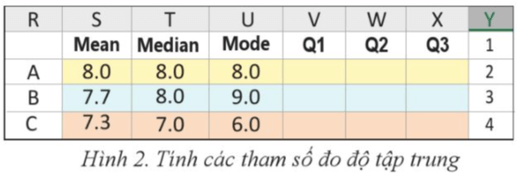
Hoạt động 1 trang 76 Chuyên đề Tin học 12: Em hãy sử dụng Excel để tính số trung bình cộng, mốt và số trung vị của ba mẫu A, B và C cho ở Hình 1 để nhận được kết quả như Hình 2.

Lời giải:

Em sử dụng Excel để tính số trung bình cộng, mốt và số trung vị của ba mẫu A, B và C cho ở Hình 1 để nhận được kết quả như Hình 2 như sau:

- Nhập dữ liệuđầu vào:

Mở Excel và nhập dữ liệu điểm của ba mẫu A, B và C vào từng cột tương ứng.

- Tính số trung bình cộng (Mean):

Sử dụng hàm =AVERAGE() để tính số trung bình cộng cho mỗi mẫu.

- Tìm mốt (Mode):

Sử dụng hàm =MODE.SNGL() để tìm giá trị xuất hiện nhiều nhất.

- Tính số trung vị (Median):

Sử dụng hàm =MEDIAN() để tính số trung vị.

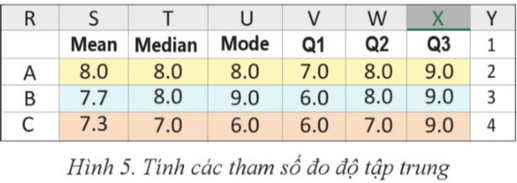
Hoạt động 2 trang 78 Chuyên đề Tin học 12: Em hãy sử dụng Excel để tính tứ phân vị của ba mẫu dữ liệu A, B và C cho ở Hình 1 để nhận được kết quả như Hình 5. Từ đó rút ra các nhận xét về sự phân bố dữ liệu dựa trên tứ phân vị.

Lời giải:

Em sử dụng Excel để tính tứ phân vị của ba mẫu dữ liệu A, B và C cho ở Hình 1 để nhận được kết quả như Hình 5 như sau:

1. Nhập dữ liệu đầu vào:

Mở Excel và nhập dữ liệu của ba mẫu A, B và C vào từng cột tương ứng.

2. Tính tứ phân vị:

Sử dụng hàm “=QUARTILE.INC(array,quart)” hoặc “=QUARTILE.EXC(array, quart)” để tính tứ phân vị.

Array là dãy dữ liệu cần tính, và quart là số thứ tự của phân vị (0, 1, 2, 3, 4).

* Nhận xét về sự phân bố dữ liệu dựa trên tứ phân vị như sau:

So sánh Q1, Q2 (trung vị), và Q3 để xem sự phân bố dữ liệu.

Nếu Q1 gần Q2 hơn Q3, dữ liệu có xu hướng tập trung ở phía dưới.

Nếu Q3 gần Q2 hơn Q1, dữ liệu có xu hướng tập trung ở phía trên.

Nếu Q1, Q2, và Q3 cách đều nhau, dữ liệu phân bố đều.

Dựa trên mô tả hình ảnh, mẫu A có sự phân bố đều với Q1, Q2, và Q3 cách đều nhau. Mẫu B và C có sự phân bố không đều với Q1 cách xa Q2 hơn so với Q3, cho thấy dữ liệu tập trung nhiều hơn ở phía trên.

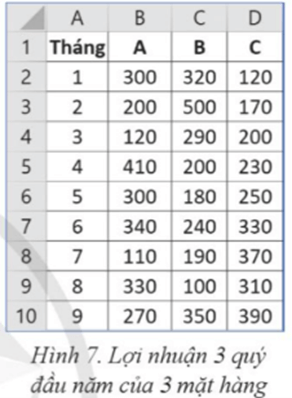
Vận dụng trang 80 Chuyên đề Tin học 12: Bảng tính ở Hình 7 ghi lại lợi nhuận 3 quý đầu năm của 3 mặt hàng A, B, C trong một đơn vị kinh doanh (đơn vị là triệu đồng). Coi mỗi cột giá trị là một mẫu số liệu. Hãy tính các tham số đo độ tập trung dữ liệu của ba mẫu A, B, C và nêu nhận xét dựa vào kết quả tính các tham số này.

Em có thể lựa chọn tập dữ liệu khác làm mẫu số liệu cần khám phá độ tập trung dữ liệu, ví dụ về chỉ số sức khỏe, giá chứng khoán, yếu tố thời tiết trong một chuỗi ngày cần quan tâm.

Lời giải:

Bảng tính ở Hình 7 ghi lại lợi nhuận 3 quý đầu năm của 3 mặt hàng A, B, C trong một đơn vị kinh doanh (đơn vị là triệu đồng). Coi mỗi cột giá trị là một mẫu số liệu. Em tính các tham số đo độ tập trung dữ liệu của ba mẫu A, B, C như sau:

1. Nhập dữ liệu đầu vào:Mở Excel và nhập dữ liệu lợi nhuận của ba mẫu A, B, và C vào từng cột tương ứng.

2. Tính tham số đo độ tập trung:

Sử dụng hàm =AVERAGE() để tính trung bình cộng.

Sử dụng hàm =MEDIAN() để tính trung vị.

Sử dụng hàm =MODE.SNGL() để tìm mốt.

Sử dụng hàm =STDEV.P() hoặc =STDEV.S() để tính độ lệch chuẩn.

3. Nhận xét dựa vào kết quả tính các tham số này như sau:

So sánh trung vị, trung bình cộng và mốt để đánh giá sự phân bố dữ liệu.

Độ lệch chuẩn càng nhỏ cho thấy dữ liệu càng tập trung quanh trung bình cộng.

Câu hỏi tự kiểm tra trang 80 Chuyên đề Tin học 12: Trong các câu sau, những câu nào đúng về các hàm tính độ tập trung dữ liệu?

a) Cách duy nhất để tính số trung bình của mẫu số liệu là sử dụng hàm AVERAGE.

b) Hàm MODE có thể cho kết quả #N/A.

c) Sử dụng được hàm MEDIAN để tính tứ phân vị thứ hai (Q,).

d) Hàm QUARTILE. EXC tính được tứ phân vị thứ 0 và thứ 4, tương ứng cho kết quả giống hàm MIN và MAX.

Lời giải:

Những câu sau đúng về các hàm tính độ tập trung dữ liệu: là b, c, và d. Cụ thể như sau:

a) Câu này Sai.

Vì mặc dù hàm AVERAGE là một cách phổ biến để tính số trung bình của mẫu số liệu, nhưng không phải là cách duy nhất. Ngoài ra, ta cũng có thể tính trung bình bằng cách khác như sử dụng tổng (SUM) chia cho số lượng (COUNT) các giá trị.

b) Câu này Đúng.

Vì hàm MODE hoặc MODE.SNGL có thể trả về kết quả là #N/A nếu không có giá trị nào xuất hiện nhiều lần trong mẫu số liệu.

c) Câu này Đúng.

Vì hhàm MEDIAN có thể được sử dụng để tính tứ phân vị thứ hai (Q2), còn được biết đến là số trung vị.

d) Câu này Đúng.

Vì hàm QUARTILE.EXC có thể tính được tứ phân vị thứ 0 và thứ 4, và chúng tương ứng với kết quả của hàm MIN và MAX. Tức là tứ phân vị thứ 0 là giá trị nhỏ nhất và tứ phân vị thứ 4 là giá trị lớn nhất của mẫu số liệu.