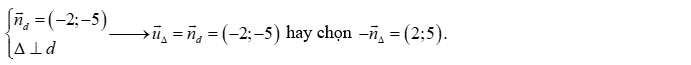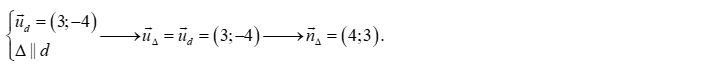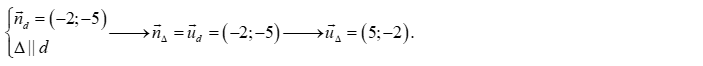Chuyên đề Phương pháp tọa độ trong mặt phẳng lớp 10 (Kết nối tri thức) | Chuyên đề dạy thêm Toán 10

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Kết nối tri thức bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Phương pháp tọa độ trong mặt phẳng

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM

DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƯƠNG, VECTƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG, HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG

Câu 1: Trong mặt phẳng $Oxy$, đường thẳng $\left(d\right):ax+by+c=0,\left(a^2+b^2\ne 0\right)$. Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng $\left(d\right)$?

A. $\overrightarrow{n}=\left(a;-b\right)$

B. $\overrightarrow{n}=\left(b;a\right)$

C. $\overrightarrow{n}=\left(b;-a\right)$

D. $\overrightarrow{n}=\left(a;b\right)$

Lời giải

Chọn D

Ta có một vectơ pháp tuyến của đường thẳng $\left(d\right)$ là $\overrightarrow{n}=\left(a;b\right)$.

Do đó chọn đáp án D. $\overrightarrow{n_1}=\left(-a;b\right).$

Câu 2: Cho đường thẳng $d$ có một vectơ pháp tuyến là $\stackrel{\rightharpoonup }{n}=\left(a;b\right)$, $a,b\in ℝ$. Xét các khẳng định sau:

1. Nếu $b=0$ thì đường thẳng $d$ không có hệ số góc.

2. Nếu $b\ne 0$ thì hệ số góc của đường thẳng $d$ là $\frac{a}{b}$.

3. Đường thẳng $d$ có một vectơ chỉ phương là $\stackrel{\rightharpoonup }{u}=\left(b;-a\right)$.

4. Vectơ $k\overrightarrow{n}$, $k\in ℝ$ là vectơ pháp tuyến của $d$.

Có bao nhiêu khẳng định sai?

A. 3

B. 2

C. 1

D. 4

Lời giải

Chọn B

$d$ có một vectơ pháp tuyến là $\stackrel{\rightharpoonup }{n}=\left(a;b\right)\Rightarrow$ phương trình $d:ax+by+c=0$.

Nếu $b=0$ thì đường thẳng $d:ax+c=0$ không có hệ số góc $\Rightarrow$ khẳng định 1 đúng.

Nếu $b\ne 0$ thì đường thẳng $d:y=-\frac{a}{b}x-\frac{c}{b}$ có hệ số góc là $-\frac{a}{b}\Rightarrow$khẳng định 2 sai.

Với $\stackrel{\rightharpoonup }{u}=\left(b;-a\right)\Rightarrow \stackrel{\rightharpoonup }{u}.\stackrel{\rightharpoonup }{n}=0\Rightarrow \stackrel{\rightharpoonup }{u}\perp \stackrel{\rightharpoonup }{n}$ là một vectơ chỉ phương của $d\Rightarrow$ khẳng định 3 đúng.

Chọn $k=0\in ℝ\Rightarrow k\overrightarrow{n}=\left(0;0\right)$ không phải là vectơ pháp tuyến của $d\Rightarrow$khẳng định 4 sai.

Vậy có 2 mệnh đề sai.

Câu 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng $d:x-2y+3=0$. Vectơ pháp tuyến của đường thẳng $d$ là

A. $\overrightarrow{n}=\left(1;-2\right)$

B. $\overrightarrow{n}=\left(2;1\right)$

C. $\overrightarrow{n}=\left(-2;3\right)$

D. $\overrightarrow{n}=\left(1;3\right)$

Lời giải

Chọn A

Câu 4: Cho đường thẳng $\left(d\right):3x+2y-10=0$. Véc tơ nào sau đây là véctơ chỉ phương của $\left(d\right)$?

A. $\overrightarrow{u}=\left(3;2\right)$

B. $\overrightarrow{u}=\left(3;-2\right)$

C. $\overrightarrow{u}=\left(2;-3\right)$

D. .$\overrightarrow{u}=\left(-2;-3\right)$

Lời giải

Chọn C

Đường thẳng $\left(d\right)$ có một véctơ pháp tuyến là $\overrightarrow{n}=\left(3;2\right)$ nên $\left(d\right)$ có một véctơ chỉ phương là $\overrightarrow{u}=\left(2;-3\right)$.

Câu 5: Cho đường thẳng:

một vectơ pháp tuyến của đường thẳng $\Delta$ có tọa độ

A. $\left(5;-3\right)$

B. $\left(6;1\right)$

C. $\left(\frac{1}{2};3\right)$

D. $\left(-5;3\right)$

Lời giải

Chọn B

có một vectơ chỉ phương là $\overrightarrow{u}=\left(-\frac{1}{2};3\right)$

suy ra có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;\frac{1}{2}\right)$

Do đó đường thẳng $\Delta$ cũng có một vectơ pháp tuyến có tọa độ $\left(6;1\right)$.

Câu 6: Trong hệ trục tọa độ $Oxy$, Véctơ nào là một véctơ pháp tuyến của đường thẳng $d$

A. $\overrightarrow{n}\left(-2;-1\right)$

B. $\overrightarrow{n}\left(2;-1\right)$

C. $\overrightarrow{n}\left(-1;2\right)$

D. $\overrightarrow{n}\left(1;2\right)$

Lời giải

Chọn A

Một VTCP của đường thẳng $d$ là $\overrightarrow{u}\left(-1;2\right)\Rightarrow$ một VTPT của $d$ là $\overrightarrow{n}\left(-2;-1\right)$.

Câu 7: Vectơ chỉ phương của đường thẳng $d:$

A. .$\overrightarrow{u}=\left(-4;3\right)$

B. $\overrightarrow{u}=\left(4;3\right)$

C. $\overrightarrow{u}=\left(3;4\right)$

D. $\overrightarrow{u}=\left(1;-2\right)$

Lời giải

Chọn A

Đường thẳng d:

có vectơ chỉ phương là $\overrightarrow{u}=\left(-4;3\right)$.

Câu 8: Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục $Ox$:

A. $\overrightarrow{u}=\left(1;0\right)$

B. $\overrightarrow{u}=(1;-1)$

C. $\overrightarrow{u}=(1;1)$

D. $\overrightarrow{u}=(0;1)$

Lời giải

Chọn A

Vector $\overrightarrow{i}=(1;0)$ là một vector chỉ phương của trục $Ox$

Các đường thẳng song song với trục $Ox$ có 1 vector chỉ phương là $\overrightarrow{u}=\overrightarrow{i}=(1;0)$

Câu 9: Cho đường thẳng $d:7x+3y-1=0$. Vectơ nào sau đây là Vectơ chỉ phương của d?

A. $\overrightarrow{u}=\left(7;3\right)$

B. $\overrightarrow{u}=\left(3;7\right)$

C. $\overrightarrow{u}=\left(-3;7\right)$

D. $\overrightarrow{u}=\left(2;3\right)$

Lời giải

Chọn C

Đường thẳng d có 1 VTPT là $\overrightarrow{n}=\left(7;3\right)$ nên d có 1 VTCP là $\overrightarrow{u}=\left(-3;7\right)$.

Câu 10: Cho đường thẳng $d:2x+3y-4=0$. Véctơ nào sau đây là véctơ pháp tuyến của đường thẳng $d$?

A. $\overrightarrow{n_1}=\left(3;2\right)$

B. $\overrightarrow{n_1}=\left(-4;-6\right)$

C. .$\overrightarrow{n_1}=\left(2;-3\right)$

D. $\overrightarrow{n_1}=\left(-2;3\right)$

Lời giải

Chọn B

Véctơ pháp tuyến của đường thẳng $d$: $\overrightarrow{n_1}=\left(-4;-6\right)$.

Câu 11: Cho đường thẳng $d:5x+3y-7=0.$ Vectơ nào sau đây là một vec tơ chỉ phương của đường thẳng $d$?

A. $\overrightarrow{n_1}=\left(3;5\right)$

B. $\overrightarrow{n_2}=\left(3;-5\right)$

C. $\overrightarrow{n_3}=\left(5;3\right)$

D. $\overrightarrow{n_4}=\left(-5;-3\right)$

Lời giải

Chọn D

Đường thẳng $d:5x+3y-7=0$ có vec tơ pháp tuyến là: $\overrightarrow{n}=\left(5;3\right).$

Ta có: $\overrightarrow{n}.\overrightarrow{n_2}=0.$

$\Rightarrow d$ có một vec tơ chỉ phương là $\overrightarrow{n_2}=\left(3;-5\right).$

Câu 12: Cho đường thẳng $\Delta :x-2y+3=0$ . Véc tơ nào sau đây không là véc tơ chỉ phương của $\Delta$?

A. $\overrightarrow{u}=\left(4;-2\right)$

B. $\overrightarrow{v}=\left(-2;-1\right)$

C. $\overrightarrow{m}=\left(2;1\right)$

D. $\overrightarrow{q}=\left(4;2\right)$

Lời giải

Chọn A

Nếu $\overrightarrow{u}$ là một véc tơ chỉ phương của đường thẳng $\Delta$ thì $k.\overrightarrow{u},\forall k\ne 0$ cũng là véc tơ chỉ phương của đường thẳng $\Delta$.

Từ phương trình đường thẳng $\Delta$ ta thấy đường thẳng $\Delta$ có một véc tơ chỉ phương có toạ độ là $\left(2;1\right)$. Do đó véc tơ $\overrightarrow{u}=\left(4;-2\right)$ không phải là véc tơ chỉ phương của $\Delta$.

Câu 13: Cho hai điểm $A=\left(1;2\right)$ và $B=\left(5;4\right)$. Vectơ pháp tuyến của đường thẳng $AB$ là

A. $\left(-1;-2\right)$

B. $\left(1;2\right)$

C. $\left(-2;1\right)$

D. $\left(-1;2\right)$

Lời giải

Chọn D

Ta có $\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)$ suy ra vectơ pháp tuyến của đường thẳng $AB$ là $\overrightarrow{n_{AB}}=\left(-1;2\right)$.

Câu 14: Cho đường thẳng $d:7x+3y-1=0$. Vectơ nào sau đây là Vectơ chỉ phương của đường thẳng d?

A. $\overrightarrow{u}=\left(7;3\right)$

B. $\overrightarrow{u}=\left(3;7\right)$

C. $\overrightarrow{u}=\left(-3;7\right)$

D. $\overrightarrow{u}=\left(2;3\right)$

Lời giải

Chọn C

Đường thẳng d có 1 VTPT là $\overrightarrow{n}=\left(7;3\right)$ nên d có 1 VTCP là $\overrightarrow{u}=\left(-3;7\right)$

Câu 15: Vectơ nào dưới đây là một vectơ pháp tuyến của $d:x-2y+2018=0$?

A. ${\overrightarrow{n}}_1\left(0;-2\right)$

B. ${\overrightarrow{n}}_3\left(-2;0\right)$

C. ${\overrightarrow{n}}_4\left(2;1\right)$

D. ${\overrightarrow{n}}_2\left(1;-2\right)$

Lời giải

Chọn D

Đường thẳng $d:x-2y+2018=0$ có vectơ pháp tuyến là ${\overrightarrow{n}}_2\left(1;-2\right)$.

Câu 16: Vectơ nào trong các vectơ dưới đây là vectơ pháp tuyến của đường thẳng $y+2x-1=0$?

A. $\left(2;-1\right)$

B. $\left(1;2\right)$

C. $\left(-2;1\right)$

D. $\left(-2;-1\right)$

Lời giải

Chọn D

$\left(d\right):y+2x-1=0\iff 2x+y-1=0$;

$\left(d\right)$ có VTPT là $\overrightarrow{n}=\left(2;1\right)$ hay ${\overrightarrow{n}}^{/}=\left(-2;-1\right)$

Câu 17: Trong mặt phẳng $Oxy$, cho đường thẳng $d:2x-y+1=0$ , một véctơ pháp tuyến của $d$ là

A. $\left(-2;-1\right)$.

B. $\left(2;-1\right)$.

C. $\left(-1;-2\right)$.

D. $\left(1;-2\right)$.

Lời giải

Chọn B

Một véctơ pháp tuyến của đường thẳng $d$ là $\overrightarrow{n}=\left(2;-1\right)$.

Câu 18: Trong mặt phẳng với hệ tọa độ $Oxy$ cho đường thẳng $d:2x-3y+4=0$. Vectơ nào sau đây là một vectơ chỉ phương của d.

A. $\overrightarrow{u_4}=\left(3;-2\right)$.

B. $\overrightarrow{u_2}=\left(2;3\right)$ .

C. $\overrightarrow{u_1}=\left(2;-3\right)$.

D. $\overrightarrow{u_3}=\left(3;2\right)$

Lời giải

Chọn D

Ta thấy đường thẳng $d$ có một vectơ pháp tuyến là $\left(2;-3\right)$. Do đó $\overrightarrow{u_3}=\left(3;2\right)$ là một vectơ chỉ phương của d.

Câu 19: Vectơ nào sau đây là một Vectơ chỉ phương của đường thẳng $\Delta :6x-2y+3=0$?

A. $\overrightarrow{u}\left(1;3\right)$

B. $\overrightarrow{u}\left(6;2\right)$

C. $\overrightarrow{u}\left(-1;3\right)$

D. $\overrightarrow{u}\left(3;-1\right)$

Lời giải

Chọn A

+) Một véctơ pháp tuyến của đường thẳng $\Delta$ là $\overrightarrow{n}\left(6;-2\right)$ nên véctơ chỉ phương của đường thẳng $\Delta$ là $\overrightarrow{u}\left(1;3\right)$.

Câu 20: Cho hai điểm $M\left(2;3\right)$ và $N\left(-2;5\right)$. Đường thẳng $MN$ có một vectơ chỉ phương là:

A. $\overrightarrow{u}=\left(4;2\right)$

B. $\overrightarrow{u}=\left(4;-2\right)$

C. $\overrightarrow{u}=\left(-4;-2\right)$

D. $\overrightarrow{u}=\left(-2;4\right)$

Lời giải

Chọn B

$\overrightarrow{MN}=\left(-4;2\right)$

Do đó vectơ chỉ phương của $MN$ là $\overrightarrow{u}=\left(4;-2\right)$.

Câu 21: Trong mặt phẳng với hệ tọa độ $Oxy,$ cho đường thẳng $d:x-2y+1=0.$ Một vectơ chỉ phương của đường thẳng $d$ là

A. $\overrightarrow{u}=\left(1;-2\right)$

B. $\overrightarrow{u}=\left(2;1\right)$

C. $\overrightarrow{u}=\left(2;-1\right)$

D. $\overrightarrow{u}=\left(1;2\right)$

Lời giải

ChọnB

Đường thẳng $d:x-2y+1=0$ có vectơ pháp tuyến là $\overrightarrow{n}=(1;-2)$

$\Rightarrow$Vectơ chỉ phương của $d$ là $\overrightarrow{u}=(2;1)$.

Câu 22: Đường thẳng $d$ có một vectơ chỉ phương là $\overrightarrow{u}=\left(2;-1\right)$. Trong các vectơ sau, vectơ nào là một vectơ pháp tuyến của $d$?

A. $\overrightarrow{n_1}=\left(-1;2\right).$

B.$\overrightarrow{n_2}=\left(1;-2\right).$

C. $\overrightarrow{n_3}=\left(-3;6\right).$

D. $\overrightarrow{n_4}=\left(3;6\right).$

Lời giải

Đường thẳng d có VTCP: $\overrightarrow{u}\left(2;-1\right)$

$\to$VTPT $\overrightarrow{n}\left(1;2\right)$ hoặc $3\overrightarrow{n}=\left(3;6\right).$

Chọn D

Câu 23: Đường thẳng $d$ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(4;-2\right)$. Trong các vectơ sau, vectơ nào là một vectơ chỉ phương của $d$?

A. $\overrightarrow{u_1}=\left(2;-4\right).$

B. $\overrightarrow{u_2}=\left(-2;4\right).$

C. $\overrightarrow{u_3}=\left(1;2\right).$

D. $\overrightarrow{u_4}=\left(2;1\right).$

Lời giải

Đường thẳng d có VTPT: $\overrightarrow{n}\left(4;-2\right)$

$\to$ VTCP $\overrightarrow{u}\left(2;4\right)$ hoặc $\frac{1}{2}\overrightarrow{u}=\left(1;2\right).$

Chọn C

Câu 24: Đường thẳng $d$ có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;-4\right)$. Đường thẳng $\Delta$ vuông góc với $d$ có một vectơ pháp tuyến là:

A. $\overrightarrow{n_1}=\left(4;3\right).$

B. $\overrightarrow{n_2}=\left(-4;-3\right).$

C. $\overrightarrow{n_3}=\left(3;4\right).$

D. $\overrightarrow{n_4}=\left(3;-4\right).$

Lời giải

Chọn D

Câu 25: Đường thẳng $d$ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(-2;-5\right)$. Đường thẳng $\Delta$ vuông góc với $d$ có một vectơ chỉ phương là:

A. $\overrightarrow{u_1}=\left(5;-2\right).$

B. $\overrightarrow{u_2}=\left(-5;2\right).$

C. $\overrightarrow{u_3}=\left(2;5\right).$

D. $\overrightarrow{u_4}=\left(2;-5\right).$

Lời giải

Chọn C

Câu 26: Đường thẳng $d$ có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;-4\right)$. Đường thẳng $\Delta$ song song với $d$ có một vectơ pháp tuyến là:

A. $\overrightarrow{n_1}=\left(4;3\right).$

B. $\overrightarrow{n_2}=\left(-4;3\right).$

C. $\overrightarrow{n_3}=\left(3;4\right).$

D. $\overrightarrow{n_4}=\left(3;-4\right).$

Lời giải

Chọn A

Câu 27: Đường thẳng $d$ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(-2;-5\right)$. Đường thẳng $\Delta$ song song với $d$ có một vectơ chỉ phương là:

A. $\overrightarrow{u_1}=\left(5;-2\right).$

B. $\overrightarrow{u_2}=\left(-5;-2\right).$

C.$\overrightarrow{u_3}=\left(2;5\right).$

D. $\overrightarrow{u_4}=\left(2;-5\right).$

Lời giải

Chọn A

DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN

Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua

Câu 28: Trên mặt phẳng tọa độ $Oxy$, cho hai điểm $A\left(-2;3\right)$ và $B\left(4;-1\right)$. Phương trình nào sau đây là phương trình đường thẳng $AB$?

A. $x+y-3=0$

B. $y=2x+1$

C. $\frac{x-4}{6}=\frac{y-1}{-4}$

Lời giải

Chọn D

Bốn phương trình đã cho trong bốn phương án đều là phương trình của đường thẳng.

Thay lần lượt tọa độ của $A,B$ vào từng phương án ta thấy tọa độ của cà $A$ và $B$ đều thỏa phương án .

Câu 29: Phương trình tham số của đường thẳng đi qua hai điểm $A\left(2;-1\right)$ và $B\left(2;5\right)$ là

Lời giải

Chọn D

Vectơ chỉ phương $\overrightarrow{AB}=\left(0;6\right)$.

Phương trình đường thẳng $AB$ đi qua $A$ và có vecto chỉ phương $\overrightarrow{AB}=\left(0;6\right)$ là:

Câu 30: Trong mặt phẳng toạ độ $Oxy$, cho hai điểm $A\left(3;-1\right)$ và $B\left(-6;2\right)$. Phương trình nào dưới đây không phải là phương trình tham số của đường thẳng $AB$?

Lời giải

Chọn B

· Cách 1: Thay tọa độ các điểm $A,B$ lần lượt vào các phương trình trong các phương án trên thì thấy phương án B không thỏa mãn.

· Cách 2: Nhận thấy rằng các phương trình ở các phương án A, C, D thì vectơ chỉ phương của các đường thẳng đó cùng phương, riêng chỉ có phương án B thì không. Do đó lựa Chọn B

Câu 31: Phương trình tham số của đường thẳng qua $M\left(1;-2\right)$, $N\left(4;3\right)$ là

Lời giải

Chọn D

Đường thẳng có véctơ chỉ phương là $\overrightarrow{MN}=\left(3;5\right)$ và đi qua $M\left(1;-2\right)$ nên có phương trình tham số là

Câu 32: Phương trình tham số của đường thẳng đi qua hai điểm là

Lời giải

Chọn B

Ta có: $\overrightarrow{AB}=\left(-9;3\right)\Rightarrow \overrightarrow{u_{AB}}=\left(3;-1\right).$

Suy ra phương trình tham số của đường thẳng AB là $\left\{\begin{array}{l}x=3+3t\\ y=-1-t\end{array}\right.$ .

Câu 33: Trong mặt phẳng tọa độ, cho hai điểm $A\left(3;0\right),B\left(0;2\right)$ và đường thẳng d: x + y = 0. Lập phương trình tham số của đường thẳng $\Delta$ qua A và song song với d.

A. $\left\{\begin{array}{l}x=t\\ y=3-t\end{array}\right.$ .

B. $\left\{\begin{array}{l}x=t\\ y=3+t\end{array}\right.$ .

C. $\left\{\begin{array}{l}x=-t\\ y=3-t\end{array}\right.$ .

D. $\left\{\begin{array}{l}x=-t\\ y=3+t\end{array}\right.$ .

Lời giải

Chọn A

Ta có $\Delta$ song song với d nên $\Delta :x+y+C=0\left(C\ne 0\right)$

$\Delta$qua A(3;0), suy ra $3+0+C=0\iff C=-3$

Như vậy $\Delta :x+y-3=0$

Vậy $\Delta$ có phương trình tham số: $\left\{\begin{array}{l}x=t\\ y=3-t\end{array}\right.$ .

Câu 34: Cho đường thẳng d có phương trình tham số $\left\{\begin{array}{l}x=5+t\\ y=-9-2t\end{array}\right.$. Phương trình tổng quát của đường thẳng d là

A. 2x + y - 1 = 0.

B. -2x + y - 1 = 0.

C. x + 2y + 1 = 0.

D. 2x + 3y - 1 = 0.

Lời giải

Chọn A

Đường thẳng $\left(d\right):\left\{\begin{array}{l}x=5+t\\ y=-9-2t\end{array}\right.$ $\iff \left\{\begin{array}{l}t=x-5\\ y=-9-2t\end{array}\right.$ $\Rightarrow y=-9-2\left(x-5\right)$ $\iff 2x+y-1=0$ .

Câu 35: Trong mặt phẳng Oxy cho điểm M(1;2). Gọi A, B là hình chiếu của M lên Ox, Oy. Viết phương trình đường thẳng AB.

A. x + 2y - 1 = 0.

B. 2x + y + 2 = 0.

C. 2x + y - 2 = 0.

D. x + y - 3 = 0.

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

Xem thêm chuyên đề dạy thêm Toán 10 hay, chi tiết khác:

Chuyên đề Vectơ

Chuyên đề Các số đặc trưng của mẫu số liệu không ghép nhóm

Chuyên đề Hàm số, đồ thị và ứng dụng

Chuyên đề Đại số tổ hợp

Chuyên đề Tính xác suất theo định nghĩa cổ điển