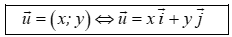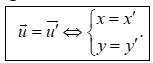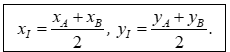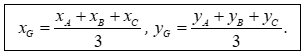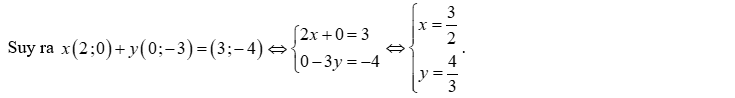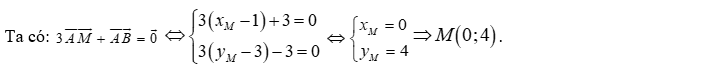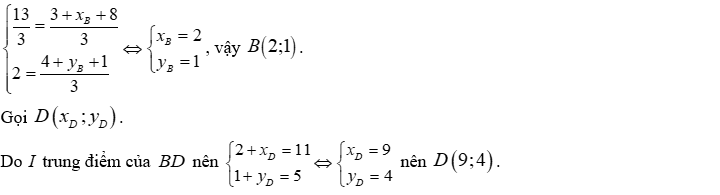Chuyên đề Phương pháp tọa độ trong mặt phẳng lớp 10 (Cánh diều) | Chuyên đề dạy thêm Toán 10

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Cánh diều bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

BÀI 1: TỌA ĐỘ CỦA VECTƠ
BÀI 2: BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

Nhắc lại hệ tọa độ:

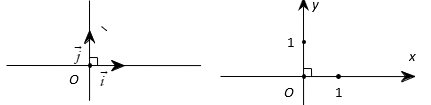
Hệ trục tọa độ $\left(O;\overrightarrow{i},\overrightarrow{j}\right)$ gồm hai trục $\left(O;\overrightarrow{i}\right)$ và $\left(O;\overrightarrow{j}\right)$ vuông góc với nhau.

Điểm gốc $O$ chung của hai trục gọi là gốc tọa độ. Trục $\left(O;\overrightarrow{i}\right)$ được gọi là trục hoành và kí hiệu là $Ox,$ trục $\left(O;\overrightarrow{j}\right)$ được gọi là trục tung và kí hiệu là $Oy$. Các vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$ là các vectơ đơn vị trên $Ox$ và $Oy$ và $\left|\overrightarrow{i}\right|=\left|\overrightarrow{j}\right|=1.$Hệ trục tọa độ $\left(O;\overrightarrow{i},\overrightarrow{j}\right)$ còn được kí hiệu là $Oxy$

Mặt phẳng mà trên đó đã cho một hệ trục tọa độ $Oxy$ còn được gọi là mặt phẳng tọa độ $Oxy$

Hay gọi tắt là mặt phẳng $Oxy$

I. TỌA ĐỘ CỦA MỘT ĐIỂM

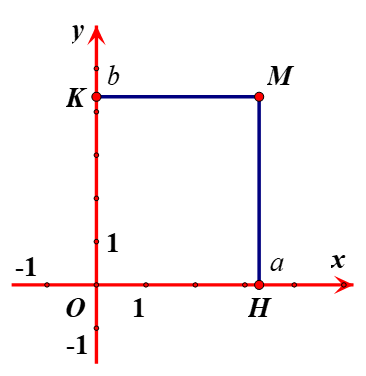
Trong mặt phẳng tọa độ $Oxy$ cho một điểm $M$ tùy ý.

Từ $M$ kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm $H$ ứng với số $a$. Số $a$ là hoành độ của điểm $M$.

Từ $M$ kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm $K$ ứng với số $b$. Số $b$ là tung độ của điểm $M$.

Cặp số $\left(a;b\right)$ là tọa độ của điểm $M$ trong mặt phẳng tọa độ $Oxy$.

Ta kí hiệu là $M\left(a;b\right)$

I. TỌA ĐỘ VECTƠ

Tọa độ của điểm $M$ là tọa độ của vectơ $\overrightarrow{OM}$.

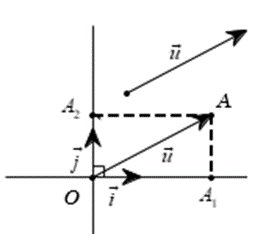
Trong mặt phẳng $Oxy$ cho một vectơ $\overrightarrow{u}$ tùy ý. Vẽ $\overrightarrow{OA}=\overrightarrow{u}$. Với mỗi vectơ $\overrightarrow{u}$ ta xác định được duy nhất một điểm $A$ sao cho $\overrightarrow{OA}=\overrightarrow{u}$

Với mỗi vectơ $\overrightarrow{u}$trong mặt phẳng tọa độ $Oxy$ tọa độ của $\overrightarrow{u}$ là tọa độ của điểm $A$ sao cho $\overrightarrow{OA}=\overrightarrow{u}$

Trong mặt phẳng tọa độ $Oxy$, nếu $\overrightarrow{u}=\left(x;y\right)$ thì $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$.

Ngược lại nếu $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$ thì $\overrightarrow{u}=\left(x;y\right)$

Do đó:

Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

Nếu $\overrightarrow{u}=\left(x;y\right)$ và $\overrightarrow{u^{\text{'}}}=\left(x^{\text{'}};y^{\text{'}}\right)$ thì

Như vậy, mỗi vectơ được hoàn toàn xác định khi biết tọa độ của nó.

III. LIÊN HỆ GIỮA TOẠ ĐỘ CỦA ĐIỂM VÀ TOẠ ĐỘ CỦA VECTƠ

Cho $A(x_A;y_A),B(x_B;y_B)$

thì $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)$

IV. BIỂU THỨC TỌA ĐỘ CỦA PHÉP TOÁN VECTƠ

Cho $\overrightarrow{u}=(x;y)$; $\overrightarrow{v}=\left(x^{\text{'}};y^{\text{'}}\right)$ và số thực $k$.

Khi đó ta có :

1) $\overrightarrow{u}\pm \overrightarrow{v}=\left(x\pm x^{\text{'}};y\pm y^{\text{'}}\right)$

2) $k.\overrightarrow{u}=(kx;ky)$

3) $\overrightarrow{u}.\overrightarrow{v}=x.x^{\text{'}}+y.y^{\text{'}}$

V. TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG. TỌA ĐỘ TRỌNG TÂM CỦA TAM GIÁC

Cho đoạn thẳng $AB$ có $A\left(x_A;y_A\right),B\left(x_B;y_B\right).$ Ta dễ dàng chứng minh được tọa độ trung điểm $I\left(x_I;y_I\right)$ của đoạn thẳng $AB$ là:

Cho tam giác $ABC$ có $A\left(x_A;y_A\right),B\left(x_B;y_B\right)$,$C\left(x_C;y_C\right).$

Khi đó tọa độ của trọng tâm $G\left(x_G;y_G\right)$ của tam giác $ABC$ được tính theo công thức:

VI. BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG

Trên mặt phẳng tọa độ $Oxy$, cho hai vectơ $\overrightarrow{a}=\left(a_1;a_2\right),\overrightarrow{b}=\left(b_1;b_2\right)$.

Khi đó $\overrightarrow{a}.\overrightarrow{b}=a_1.b_1+a_2.b_2$

Ứng dụng biểu thức tọa độ của các phép toán vecto

Trên mặt phẳng tọa độ $Oxy$, cho hai vectơ $\overrightarrow{a}=\left(a_1;a_2\right),\overrightarrow{b}=\left(b_1;b_2\right)$ và hai điểm $A\left(x_A;y_A\right),B\left(x_B;y_B\right).$

Ta có:

1) $\overrightarrow{a}\perp \overrightarrow{b}\iff \overrightarrow{a}.\overrightarrow{b}=0\iff a_1{b}_1+a_2{b}_2=0$

2) $\overrightarrow{a},\overrightarrow{b}$ cùng phương $\iff a_1{b}_1-a_2{b}_2=0$

3) $\left|\overrightarrow{a}\right|=\sqrt{a_1^2+a_2^2}$

4) $AB=\left|\overrightarrow{AB}\right|=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$

5) $\cos \left(\overrightarrow{a};\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$

($\overrightarrow{a}=\left(a_1;a_2\right)$ và $\overrightarrow{b}=\left(b_1;b_2\right)$ đều khác $\overrightarrow{0}$)

Câu 1. Trên trục $\left(O;\overrightarrow{i}\right)$ cho các điểm $A,B,C$ lần lượt có tọa độ $1;-2;3$.

Tính độ dài đại số của các vectơ $\overrightarrow{AB},\overrightarrow{BC}$. Từ đó suy ra hai vectơ $\overrightarrow{AB},\overrightarrow{BC}$ ngược hướng?

Lời giải

Ta có:

$\overline{AB}=-2-1=-3$, $\overline{BC}=3-\left(-2\right)=5$.

Do đó vectơ $\overrightarrow{AB}$ ngược hướng với vectơ $\overrightarrow{i}$ và vectơ $\overrightarrow{BC}$ cùng hướng với vectơ $\overrightarrow{i}$.

Câu 2. Trong mặt phẳng tọa độ $Oxy$, cho $\overrightarrow{a}=2\overrightarrow{i}$, $\overrightarrow{b}=-3\overrightarrow{j}$, $\overrightarrow{c}=3\overrightarrow{i}-4\overrightarrow{j}$.

a) Tìm tọa độ của các vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $\overrightarrow{m}=3\overrightarrow{a}-2\overrightarrow{b}$.

b) Phân tích vectơ $\overrightarrow{c}$ theo hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$.

Lời giải

a) Ta có:

$\overrightarrow{a}=\left(2;0\right)$, $\overrightarrow{b}=\left(0;-3\right)$, $\overrightarrow{c}=\left(3;-4\right)$.

Khi đó $3\overrightarrow{a}=\left(6;0\right)$, $-2\overrightarrow{b}=\left(0;6\right)$ nên $\overrightarrow{m}=3\overrightarrow{a}-2\overrightarrow{b}=\left(6+0;0+6\right)=\left(6;6\right)$

b) Ta có hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ không cùng phương.

Theo yêu cầu của đề bài ta cần tìm bộ số $x$, $y$ thỏa mãn $\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}$

Vậy ta viết được $\overrightarrow{c}=\frac{3}{2}\overrightarrow{a}+\frac{4}{3}\overrightarrow{b}$.

Câu 3. Trong mặt phẳng tọa độ $Oxy$, cho $A\left(2;1\right)$, $B\left(-1;-2\right)$, $C\left(-3;2\right)$.

a) Tìm tọa độ trung điểm của đoạn thẳng $AC$

b) Chứng minh ba điểm $A,B,C$ tạo thành một tam giác.

c) Tìm tọa độ trọng tâm tam giác $ABC$.

Lời giải

a) Gọi $M$ là trung điểm $AC$ thì $M\left(\frac{2-3}{2};\frac{1+2}{2}\right)$ hay $M\left(\frac{-1}{2};\frac{3}{2}\right)$.

b) Tính được $\overrightarrow{AB}=\left(-3;-3\right)$, $\overrightarrow{AC}=\left(-5;1\right)$ dẫn đến hai vectơ đó không cùng phương. Nói cách khác ba điểm $A,B,C$ tạo thành một tam giác.

c) Gọi $G$ là trọng tâm tam giác ABC thì $G\left(\frac{2-1-3}{3};\frac{1-2+2}{3}\right)$ hay $G\left(-\frac{2}{3};\frac{1}{3}\right)$

Câu 4. Trong mặt phẳng tọa độ $Oxy$, cho $A\left(2;1\right)$>, $B\left(-1;-2\right)$, $C\left(-3;2\right)$

a) Tìm tọa độ điểm $E$ sao cho $C$ là trung điểm của đoạn thẳng $EB$

b) Xác định tọa độ điểm $D$ sao cho tứ giác $ABCD$ là hình bình hành.

Lời giải

a) Do $C$ là trung điểm của đoạn thẳng $EB$ nên:

Vậy $E\left(-5;6\right)$

b) Gọi

$D\left(x_D;y_D\right)\Rightarrow \overrightarrow{DC}=\left(-3-x_D;2-y_D\right)$

Do tứ giác $ABCD$ là hình bình hành nên:

Ta thấy $A,B,C,D$ không thẳng hàng.

Vậy $D\left(0;5\right)$ là đáp án bài toán.

Câu 5. Trong mặt phẳng $Oxy$, cho các điểm $A\left(1;3\right)$, $B\left(4;0\right)$. Tìm tọa độ điểm $M$ thỏa $3\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{0}$?

Lời giải

Giả sử $M\left(x_M;y_M\right)$

suy ra $\overrightarrow{AM}=\left(x_M-1;y_M-3\right)$ và $\overrightarrow{AB}=\left(3;-3\right)$

Ta có:

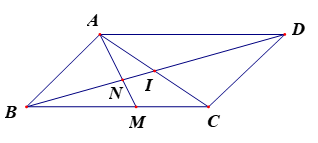
Câu 6. Trong mặt phẳng tọa độ $Oxy$, cho hình bình hành $ABCD$ có $A\left(3;4\right)$, $C\left(8;1\right)$. Gọi $M$ là trung điểm của cạnh $BC$, $N$ là giao điểm của $BD$ và $AM$. Xác định các đỉnh còn lại của hình bình hành $ABCD$, biết $N\left(\frac{13}{3};2\right)$.

Lời giải

Do $I$ là tâm của hình bình hành $ABCD$, ta có $I$ là trung điểm của đoạn thẳng $AC$nên $I\left(\frac{11}{2};\frac{5}{2}\right)$

Xét tam giác $ABC$ thì $BI$, $AM$ là hai đường trung tuyến nên $N$là trọng tâm tam giác $ABC$

Do đó:

Vậy $B\left(2;1\right),D\left(9;4\right)$

Câu 1. Trong mặt phẳng toạ độ $Oxy$, cho các điểm $M\left(1;3\right),N\left(4;2\right)$.

a) Tính độ dài của các đoạn thẳng $OM$, $ON$, $MN$.

b) Chứng minh rằng tam giác $OMN$ vuông cân.

Câu 2. Trong mặt phẳng toạ độ $Oxy$, cho các vectơ $\overrightarrow{a}=3\overrightarrow{i}-2\overrightarrow{j},\overrightarrow{b}=\left(4;-1\right)$ và các điềm $M\left(-3;6\right),N\left(3;-3\right)$

a) Tìm mối liên hệ giữa các vectơ $\overrightarrow{MN}$ và $2\overrightarrow{a}-\overrightarrow{b}$

b) Các điểm $O,M,N$ có thẳng hàng hay không?

c) Tìm điềm $P\left(x;y\right)$ để $OMNP$ là một hình bình hành.

Câu 3. Trong mặt phẳng toạ độ $Oxy$, cho các điềm $A\left(1;3\right),B\left(2;4\right),C\left(-3;2\right)$.

a) Hãy chứng minh rằng $A,B,C$ là ba đỉnh của một tam giác.

b) Tìm toạ độ trung điểm $M$ của đoạn thẳng $AB$

c) Tìm toạ độ trọng tâm $G$ của tam giác $ABC$

d) Tìm điểm $D\left(x;y\right)$ để $O\left(0;0\right)$ là trọng tâm của tam giác $ABD$

Câu 4. Sự chuyển động của một tàu thủy được thề hiện trên một mặt phẳng toạ độ như sau: Tàu khời hành từ vị trí $A\left(1;2\right)$ chuyền động thẳng đều với vận tốc (tính theo giờ) được biểu thị bời vectơ $\overrightarrow{v}=\left(3;4\right)$. Xác định vị trí của tàu (trên mặt phẳng toạ độ) tại thời điểm sau khi khởi hành $1,5$ giờ.

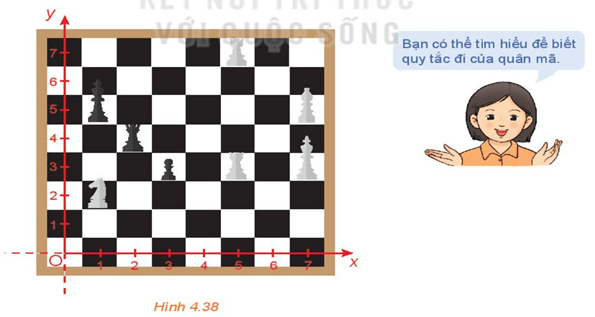
Câu 5. Trong Hình 4.38, quân mã đang ở vị trí có toạ độ $\left(1;2\right)$. Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?

DẠNG 1: TÌM TỌA ĐỘ ĐIỂM, TỌA ĐỘ VECTƠ TRÊN MẶT PHẲNG $Oxy$

Câu 1: Trong mặt phẳng tọa độ $Oxy$. Cho điểm $M\left(x;y\right)$. Tìm tọa độ của các điểm $M_1$ đối xứng với $M$ qua trục hoành?

Câu 2: Trong không gian $Oxy$, cho hai điểm $A\left(1;2\right)$, $B\left(-2;3\right)$. Tìm tọa độ của vectơ $\overrightarrow{AB}$?

Câu 3: Vectơ $\overrightarrow{a}=\left(-4;0\right)$ được phân tích theo hai vectơ đơn vị $\left(\overrightarrow{i};\overrightarrow{j}\right)$ như thế nào?

Câu 4: Trong hệ trục tọa độ $Oxy$, cho hình vuông $ABCD$ tâm I và có $A(1;3)$. Biết điểm $B$ thuộc trục $Ox$ và $\overrightarrow{BC}$ cùng hướng với $\overrightarrow{i}$. Tìm tọa độ các vectơ $\overrightarrow{AC}$?

Câu 5: Trong mặt phẳng tọa độ $Oxy$. Cho hình thoi $ABCD$ cạnh a và $\widehat{BAD}={60}^0$. Biết $A$ trùng với gốc tọa độ $O$; $C$ thuộc trục $Ox$ và $x_B\ge 0,y_B\ge 0$. Tìm tọa độ các đỉnh $B$ và $C$ của hình thoi $ABCD$

Câu 1: Trong mặt phẳng tọa độ $Oxy$, tọa độ $\overrightarrow{i}$ là

A. $\overrightarrow{i}=\left(0;0\right)$

B. $\overrightarrow{i}=\left(0;1\right)$

C. $\overrightarrow{i}=\left(1;0\right)$

D. $\overrightarrow{i}=\left(1;1\right)$

Câu 2: Trong hệ tọa độ $Oxy$ cho $A\left(5;2\right)$, $B\left(10;8\right)$. Tìm tọa độ của vectơ $\overrightarrow{AB}?$

A. $\left(15;10\right)$

B. $\left(2;4\right)$

C. $\left(5;6\right)$

D. $\left(50;16\right)$

Câu 3: Trong mặt phẳng $Oxy$ cho $A=\left(5;-2\right),B=\left(10;8\right)$. Tọa độ vectơ $\overrightarrow{AB}$ là:

A. $\overrightarrow{AB}\left(15;10\right)$

B. $\overrightarrow{AB}\left(2;4\right)$

C. $\overrightarrow{AB}\left(5;10\right)$

D. $\overrightarrow{AB}\left(50;16\right)$

Câu 4: Trong mặt phẳng toạ độ $Oxy$ cho hai điểm $A\left(1;4\right)$ và $B\left(3;5\right)$. Khi đó:

A. $\overrightarrow{AB}=\left(-2;-1\right)$

B. $\overrightarrow{BA}=\left(1;2\right)$

C. $\overrightarrow{AB}=\left(2;1\right)$

D. $\overrightarrow{AB}=\left(4;9\right)$

Câu 5: Trong mặt phẳng tọa độ $Oxy$ cho $A\left(5;3\right)$, $B\left(7;8\right)$. Tìm tọa độ của véctơ $\overrightarrow{AB}$

A. $\left(15;10\right)$

B. $\left(2;5\right)$

C. $\left(2;6\right)$

D. $\left(-2;-5\right)$

Câu 6: Trong hệ tọa độ $Oxy$cho tam giác $ABC$ có $B\left(9;7\right),C\left(11;-1\right)$. Gọi $M,N$ lần lượt là trung điểm của $AB,AC.$ Tìm tọa độ vectơ $\overrightarrow{MN}$?

A. $\left(2;-8\right)$

B. $\left(1;-4\right)$

C. $\left(10;6\right)$

D. $\left(5;3\right)$

Câu 7: Trong hệ tọa độ $Oxy,$ cho hình vuông $ABCD$ có gốc $O$ làm tâm hình vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào đúng?

A. $|\overrightarrow{OA}+\overrightarrow{OB}|=AB.$

B. $\overrightarrow{OA}-\overrightarrow{OB},\overrightarrow{DC}$ cùng hướng.

C. $x_A=-x_C,y_A=y_C.$

D. $x_B=-x_C,y_B=-y_C.$

Câu 8: Trong hệ tọa độ $Oxy,$ cho $M\left(3;-4\right)$. Gọi $M_1,M_2$ lần lượt là hình chiếu vuông góc của $M$ trên $Ox,Oy.$ Khẳng định nào đúng?

A. $\overline{O{M}_1}=-3.$

B. $\overline{O{M}_2}=4.$

C. $\overrightarrow{O{M}_1}-\overrightarrow{O{M}_2}=\left(-3;-4\right)$

D. $\overrightarrow{O{M}_1}+\overrightarrow{O{M}_2}=\left(3;-4\right)$

Câu 9: Trong hệ tọa độ $Oxy$ cho hình bình hành $OABC,C\in Ox.$ Khẳng định nào sau đây đúng?

A. $\overrightarrow{AB}$ có tung độ khác 0

B. $A,B$ có tung độ khác nhau.

C. $C$ có hoành độ khác 0

D. $x_A+x_C-x_B=0.$

Câu 10: Trong hệ trục tọa độ $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$, cho tam giác đều $ABC$ cạnh $G$, biết $O$ là trung điểm $BC$, $\overrightarrow{i}$ cùng hướng với $\overrightarrow{OC}$, $\overrightarrow{j}$ cùng hướng $\overrightarrow{OA}$. Tìm tọa độ của các đỉnh của tam giác $ABC$.Gọi $x_A,x_B,x_C$ lần lượt là hoành độ các điểm $A,B,C$. Giá trị của biểu thức $x_A+x_B+x_C$ bằng:

A. $0$

B. $\frac{a}{2}$

C. $\frac{a\sqrt{3}}{2}$

D. $-\frac{a}{2}$

Câu 11: Trong hệ trục tọa độ $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$, cho tam giác đều $ABC$ cạnh $a$, biết $O$ là trung điểm $B$, $\overrightarrow{i}$ cùng hướng với $\overrightarrow{OC}$, $\overrightarrow{j}$ cùng hướng $\overrightarrow{OA}$. Tìm tọa độ tâm đường tròn ngoại tiếp tam giác $ABC$

A. $G\left(0;\frac{a\sqrt{3}}{6}\right)$

B. $G\left(0;\frac{a\sqrt{3}}{4}\right)$

C. $G\left(\frac{a\sqrt{3}}{6};0\right)$

D. $G\left(\frac{a\sqrt{3}}{4};0\right)$

Câu 12: Trong hệ trục tọa độ $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$, cho hình thoi $ABCD$ tâm O có

$AC=8,BD=6$. Biết $\overrightarrow{OC}$ và $\overrightarrow{i}$ cùng hướng, $\overrightarrow{OB}$ và $\overrightarrow{j}$ cùng hướng. Tính tọa độ trọng tâm tam giác $ABC$

A. $G\left(0;1\right)$

B. $G\left(-1;0\right)$

C. $\left(\frac{1}{2};0\right)$

D. $\left(0;\frac{3}{2}\right)$

DẠNG 2: XÁC ĐỊNH TỌA ĐỘ ĐIỂM, VECTƠ LIÊN QUAN ĐẾN BIỂU THỨC DẠNG $\overrightarrow{u}+\overrightarrow{v},\overrightarrow{u}-\overrightarrow{v},k\overrightarrow{u}$

Câu 1: Trong không gian $Oxy$, cho hai vectơ $\overrightarrow{a}\left(1;3\right)$, $\overrightarrow{b}\left(3;-4\right)$.
Tìm tọa độ vectơ $\overrightarrow{a}-\overrightarrow{b}$?

Câu 2: Cho $\overrightarrow{a}=\left(x;2\right),\overrightarrow{b}=\left(-5;1\right),\overrightarrow{c}=\left(x;7\right)$.
Tìm $x$ để Vec tơ $\overrightarrow{c}=2\overrightarrow{a}+3\overrightarrow{b}$.

Câu 3: Cho hai điểm $A\left(1;0\right)$ và $B\left(0;-2\right)$. Tọa độ điểm $D$ sao cho $\overrightarrow{AD}=-3\overrightarrow{AB}$ là:

Câu 4: Trong mặt phẳng $Oxy$, cho các điểm $A\left(1;3\right),B\left(4;0\right)$. Tọa độ điểm $M$ thỏa $3\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{0}$ là

Câu 5: Trong mặt phẳng $Oxy$, cho các điểm $A\left(-3;3\right),B\left(1;4\right),C\left(2;-5\right)$. Tọa độ điểm $M$ thỏa mãn $2\overrightarrow{MA}-\overrightarrow{BC}=4\overrightarrow{CM}$ là:

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

Xem thêm chuyên đề dạy thêm Toán 10 hay, chi tiết khác:

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Chuyên đề Hàm số và đồ thị

Chuyên đề Hệ thức lượng trong tam giác. Vectơ

Chuyên đề Đại số tổ hợp

Chuyên đề Một số yếu tố thống kê và xác suất