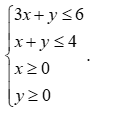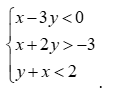Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn lớp 10 (Cánh diều) | Chuyên đề dạy thêm Toán 10

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bất phương trình bậc nhất hai ẩn $x,y$ là bất phương trình có một trong các dạng sau: $ax+by\le c;$$ax+by<c;ax+by\ge c;ax+by>c$

trong đó $a,b,c$ là những số thực đã cho, $a$ và $b$ không đồng thời bằng $0,x$ và $y$ là các ẩn số.

Cho bất phương trình bậc nhất hai ẩn $x,y$: $ax+by<c\left(1\right)$. Mỗi cặp số $\left(x_0;y_0\right)$ sao cho $a{x}_0+b{y}_0<c$ là mệnh đề đúng được gọi là một nghiệm của bất phương trình (1). Trong mặt phẳng tọa độ $Oxy$, tập hợp tất cả các điểm có tọa độ thỏa mãn bất phương trình (1) được gọi là miền nghiệm của bất phương trình (1).

II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ $Oxy$ tập hợp các điểm có tọa độ là nghiệm của bất phương trình được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình $ax+by\le c$ như sau (tương tự cho bất phương trình $ax+by\ge c$)

- Bước 1. Trên mặt phẳng tọa độ $Oxy,$ vẽ đường thẳng $\Delta :ax+by=c.$

- Bước 2. Lấy một điểm $M_0\left(x_0;y_0\right)$ không thuộc $\Delta$ (ta thường lấy gốc tọa độ $O$)

- Bước 3. Tính $a{x}_0+b{y}_0$ và so sánh $a{x}_0+b{y}_0$ với $c$

- Bước 4. Kết luận

Nếu $a{x}_0+b{y}_0<c$ thì nửa mặt phẳng bờ $\Delta$ chứa $M$ là miền nghiệm của $a{x}_0+b{y}_0\le c.$

Nếu $a{x}_0+b{y}_0>c$ thì nửa mặt phẳng bờ $\Delta$ không chứa $M$ là miền nghiệm của $a{x}_0+b{y}_0\le c.$

Chú ý:

Miền nghiệm của bất phương trình $a{x}_0+b{y}_0\le c$ bỏ đi đường thẳng $ax+by=c$ là miền nghiệm của bất phương trình $a{x}_0+b{y}_0<c.$

Câu 1: Cặp số nào sau đây là nghiệm của bất phương trình $2x-3y<3$?

a) $(0;-1)$

b) $(2;1)$

c) $(3;1)$

Câu 2: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $x+2y<3$

b) $3x-4y\ge -3$

c) $y\ge -2x+4$

d) $y<1-2x$

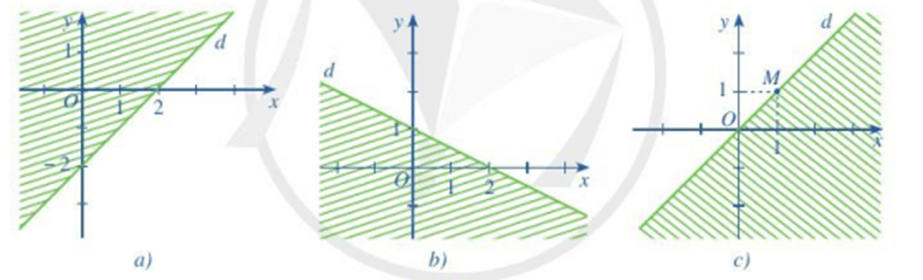
Câu 3:Phần không gạch (không kể d) ở mỗi Hình a, b, c là miền nghiệm của bất phương trình nào?

Câu 4:Một gian hàng trưng bày bàn và ghế rộng $60m^2$. Diện tích để kê một chiếc ghế là $0,5m^2$, một chiếc bàn là $1,2m^2$. Gọi x là số chiếc ghế, y là số chiếc bàn được kê.

a) Viết bất phương trình bậc nhất hai ẩn $x,y$ cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là $12m^2$

b) Chỉ ra ba nghiệm của bất phương trình trên.

Câu 5:Trong 1 lạng (100 g thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46g protein. (Nguồn:https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn $x,y$ để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) $2x+3y>6$;

b) $2^{2}x+y\le 0$;

c) $2x^2-y\ge 1$.

Câu 2. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng toạ độ:
a) $3x+2y\ge 300$;

b) $7x+20y<0$.

Câu 3. Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

a) Gọi $x$ và $y$ lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa $x$ và $y$ sao cho tổng số tiền ông An phải trả không quá $14$ triệu đồng.

b) Biểu diển miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ.

BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn $x,y$ mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau:

- Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

- Phần không bị gạch là miền nghiệm cần tìm.

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính.

Câu 1:Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.

Câu 2:Biểu diễn miền nghiệm của hệ bất phương trình:

Câu 3:Miền không bị gạch ở mỗi Hình $12a,12b$ là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

12a)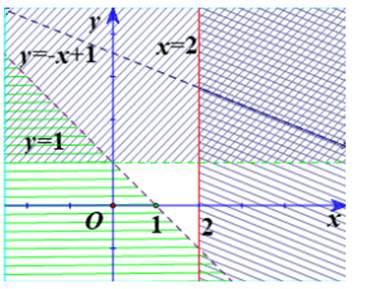

12b)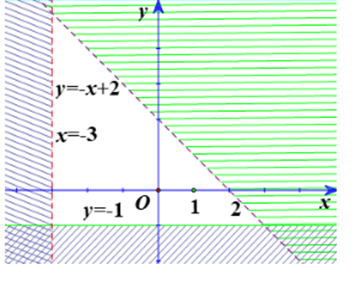

Câu 4:Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.

Câu 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

Câu 2. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:

Câu 3. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình $2x+y\le 3$.

Câu 2: Biểu diễn hình học tập nghiệm của bất phương trình $-3x+y+2\le 0$.

Câu 3: Biểu diễn hình học tập nghiệm của bất phương trình:

$x+3+2(2y+5)<2(1-x)$ .

Câu 4: Biểu diễn hình học tập nghiệm của bất phương trình:

$\left(1+\sqrt{3}\right)x-\left(1-\sqrt{3}\right)y\ge 2$

DẠNG 2: CÁC BÀI TOÁN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1: Biểu diễn hình học tập nghiệm của hệ bất phương trình:

Câu 2: Tìm miền nghiệm của hệ bất phương trình:

Câu 3: Tìm trị lớn nhất của biểu thức $F\left(x;y\right)=x+2y$, với điều kiện:

DẠNG 3: CÁC BÀI TOÁN THỰC TIỄN

Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức $T\left(x,y\right)=ax+by$ với $\left(x;y\right)$ nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước.

Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm $S$ là đa giác.

Bước 2: Tính giá trị của $F$ tương ứng với $\left(x;y\right)$ là tọa độ của các đỉnh của đa giác.

Bước 3: Kết luận:

Giá trị lớn nhất của $F$ là số lớn nhất trong các giá trị tìm được.

Giá trị nhỏ nhất của $F$ là số nhỏ nhất trong các giá trị tìm được.

Câu 1: Một hộ nông dân định trồng đậu và cà trên diện tích 800m². Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m² nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100m². Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180.

Câu 2: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?

Câu 3: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm $I$ và $II$. Mỗi sản phẩm $I$ bán lãi $500$ nghìn đồng, mỗi sản phẩm $II$ bán lãi $400$ nghìn đồng. Để sản xuất được một sản phẩm $I$ thì Chiến phải làm việc trong $3$ giờ, Bình phải làm việc trong $1$ giờ. Để sản xuất được một sản phẩm $II$ thì Chiến phải làm việc trong $2$ giờ, Bình phải làm việc trong $6$ giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá $180$ giờ và Bình không thể làm việc quá $220$ giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng.

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

Xem thêm chuyên đề dạy thêm Toán 10 hay, chi tiết khác:

Chuyên đề Hàm số và đồ thị

Chuyên đề Hệ thức lượng trong tam giác. Vectơ

Chuyên đề Đại số tổ hợp

Chuyên đề Một số yếu tố thống kê và xác suất

Chuyên đề Phương pháp tọa độ trong mặt phẳng