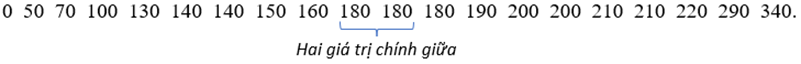Chuyên đề Một số yếu tố thống kê và xác suất lớp 10 (Cánh diều) | Chuyên đề dạy thêm Toán 10

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Cánh diều bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

BÀI 1. SỐ GẦN ĐÚNG. SAI SỐ

I. SỐ GẦN ĐÚNG: Trong nhiều trường hợp ta không thể biết hoặc khó biết số đúng (kí hiệu $\overline{a}$) mà ta chỉ tìm được giá trị khá xấp xỉ nó. Giá trị này được gọi là số gần đúng kí hiệu là

Ví dụ: giá trị gần đúng của $\pi$ là 3,14 hay 3,14159; còn đối với $\sqrt{2}$ là 1,41 hay 1,414;.

Như vậy có sự sai lệch giữa giá trị chính xác của một đại lượng và giá trị gần đúng của nó. Để đánh giá mức độ sai lệch đó, người ta đưa ra khái niệm sai số tuyệt đối.

II. SAI SỐ CỦA SỐ GẦN ĐÚNG

1) Sai số tuyệt đối

Giá trị $\left(a-\overline{a}\right)$ phản ánh mức độ sai lệch giữa số đúng $\overline{a}$ và số gần đúng $a$, được gọi là sai số tuyệt đối của số gần đúng $a$, kí hiệu là ${\Delta }_a$, tức là: ${\Delta }_a=\left(a-\overline{a}\right)$.

2) Độ chính xác của một số gần đúng

Trong thực tế, nhiều khi ta không biết $\overline{a}$ nên ta không tính được ${\Delta }_a$. Tuy nhiên ta có thể đánh giá ${\Delta }_a$ không vượt quá một số dương d nào đó.

Nếu ${\Delta }_a\le d$ thì $a-d\le \overline{a}\le a+d$, khi đó ta viết $\overline{a}=a\pm d$

$d$ gọi là độ chính xác của số gần đúng.

3) Sai số tương đối

Sai số tương đối của số gần đúng a, kí hiệu là ${\delta }_a$là tỉ số giữa sai số tuyệt đối và $\left|a\right|$,

tức là ${\delta }_a=\frac{{\Delta }_a}{\left|a\right|}$.

Nhận xét:

Nếu $\overline{a}=a\pm d$ thì ${\Delta }_a\le d$ suy ra ${\delta }_a\le \frac{d}{\left|a\right|}$_. Do đó $\frac{d}{\left|a\right|}$ càng nhỏ thì chất lượng của phép đo đặc hay tính toán càng cao.

III. SỐ QUY TRÒN. QUY TRÒN SỐ GẦN ĐÚNG

Số thu được sau khi thực hiện làm tròn số được gọi là số quy tròn. Số quy tròn là một số gần đúng của số ban đầu.

Nguyên tắc quy tròn các số như sau:

Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay chữ số đó và các chữ số bên phải nó bởi 0.

Nếu chữ số ngay sau hàng quy tròn lớn hơn hay bằng 5 thì ta thay chữ số đó và các chữ số bên phải nó bởi 0 và cộng thêm một đơn vị vào số hàng làm tròn.

Nhận xét: Khi thay số đúng bởi số qui tròn đến một hàng số nào đó thì sai số tuyệt đối của số qui tròn không vượt quá nửa đơn vị của hàng qui tròn.

Như vậy, độ chính xác của số qui tròn bằng nửa đơn vị của hàng qui tròn.

Chú ý: Các viết số quy tròn của số gần đúng căn cứ vào độ chính xác cho trước.

Cho số gần đúng $a$ với độ chính xác $d$. Khi được yêu cầu quy tròn a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn $a$ đến hàng cao nhất mà d nhỏ hơn một đơn vị của hàng đó.

Chữ số chắc (đáng tin)

Cho số gần đúng $a$ của số $\overline{a}$ với độ chính xác $d$. Trong số $a$ một chữ số được gọi là chữ số chắc (hay đáng tin) nếu $d$ không vượt quá nửa đơn vị của hàng có chữ số đó.

Nhận xét: Tất cả cá chữ số đứng bên trái chữ số chắc đều là chữ số chắc. Tất cả các chữ số đứng bên phải chữ số không chắc đều là chữ số không chắc.

Dạng chuẩn của số gần đúng

Nếu số gần đúng là số thập phân không nguyên thì dạng chuẩn là dạng mà mọi chữ số của nó đều là chữ chắc chắn.

Nếu số gần đúng là số nguyên thì dạng chuẩn của nó là: A10^k trong đó A là số nguyên, k là hàng thấp nhất có chữ số chắc $\left(k\in \mathbb{N}\right)$. (suy ra mọi chữ số của A đều là chữ số chắc chắn).

Khi đó độ chính xác $d=0,{5.10}^k$.

Kí hiệu khoa học của một số

Mọi số thập phân khác 0 đều viết được dưới dạng $\alpha {.10}^n$, $1\le \left(\alpha \right)<10$, $n\in \mathbb{N}$(Quy ước ${10}^{-n}=\frac{1}{{10}^n}$) dạng như vậy được gọi là kí hiệu khoa học của số đó.

Câu 1. Trong các số sau, những số nào là số gần đúng?

a) Cân một túi gạo cho kết quả là $10,2kg$.

b) Bán kính Trái Đất là $637km$.

c) Trái Đất quay một vòng quanh Mặt Trời mắt 365 ngày.

Câu 2. Giải thích kết quả “Đo độ cao của một ngọn núi cho kết quả là $1235\pm 5\text{m}$ ” và thực hiện làm tròn số gần đúng.

Câu 3. Sử dụng máy tính cầm tay tìm số gần đúng cho $\sqrt[3]{7}$ với độ chính xác 0,0005.

Câu 4. Các nhà vật lí sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:

67,31 $\pm$ 0,96;

67,90 $\pm$ 0,55;

67,74 $\pm$ 0,46

Phương pháp nào chính xác nhất tính theo sai số tương đối?

Câu 5. An và Bình cùng tính chu vi của hình tròn bán kính với hai kết quả như sau:

Kết quả của An:
$S_1=2\pi R=2.3,14.2=12,56\text{cm}$;

Kết quả của Bình:
$S_2=2\pi R=2.3,1.2=12,4\text{cm}$.

Hỏi:

a) Hai giá trị tính được có phải là các số gần đúng không?

b) Giá trị nào chính xác hơn?

Câu 6. Làm tròn số $8316,4$ đến hàng chục và $9,754$ đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

DẠNG 1: TÍNH SAI SỐ TUYỆT ĐỐI, ĐỘ CHÍNH XÁC CỦA MỘT SỐ GẦN ĐÚNG.

Câu 1: Kết quả đo chiều dài của một cây cầu được ghi là $152m\pm 0,2m$, điều đó có nghĩa là gì?

A. Chiều dài đúng của cây cầu là một số nằm trong khoảng từ 151,8m đến 152,2m.

B. Chiều dài đúng của cây cầu là một số lớn hơn 152 m.

C. Chiều dài đúng của cây cầu là một số nhỏ hơn 152 m.

D. Chiều dài đúng của cây cầu là 151,8 m hoặc là 152,2 m.

Câu 2: Khi tính diện tích hình tròn bán kính R = 3cm, nếu lấy $\pi =3,14$ thì độ chính xác là bao nhiêu?

A. $d=0,009$

B. $d=0,09$

C. $d=0,1$

D. $d=0,01$

Câu 3: Cho giá trị gần đúng của $\frac{8}{17}$ là 0,47. Sai số tuyệt đối của 0,47 là:

A. 0,001.

B. 0,002.

C. 0,003.

D. 0,004

DẠNG 2: SAI SỐ TƯƠNG ĐỐI CỦA SỐ GẦN ĐÚNG

Câu 4: Kết quả đo chiều dài của một cây cầu được ghi là $152m\pm 0,2m$. Tìm sai số tương đối của phép đo chiều dài cây cầu.

A. ${\delta }_a<0,1316\%$

B. ${\delta }_a<1,316\%$

C. ${\delta }_a=0,1316\%$

D. ${\delta }_a>0,1316\%$

Câu 5: Bạn A đo chiều dài của một sân bóng ghi được $250\pm 0,2m$. Bạn B đo chiều cao của một cột cờ được $15\pm 0,1m$. Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong phép đo của bạn đó là bao nhiêu?

A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.

B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.

C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.

D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%.

Câu 6: Hãy xác định sai số tuyệt đối của số $a=123456$ biết sai số tương đối ${\delta }_a=0,2\%$

A. 146,912.

B. 617280.

C. 24691,2.

D. 61728000

DẠNG 3 : QUY TRÒN SỐ GẦN ĐÚNG

PHƯƠNG PHAP GIẢI

Tùy theo mức độ cho phép, ta có thể quy tròn một số đếm đến hàng đơn vị, hang chục, hang trăm,… hay đến hàng phần chục, hàng phần trăm,… (gọi là hàng quy tròn) theo nguyên tắc sau:

Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0.

Nếu chữ số ngay sau hàng quy tròn lớn hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0 và cộng thêm một đơn vị ở chữ số ở hàng quy tròn.

Ví dụ: Các số quy tròn của số x theo từng hàng cho trongbảng sau:

Nhận xét:

Khi thay số đúng bởi số quy tròn thì sai số tuyệt đối không vượt quá nửa đơn vị của hàng quy tròn.

Nếu $\overline{a}=a\pm d$ thì ta quy tròn số đến hàng lớn hơn hàng của $d$ một đơn vị.

Câu 7: Tìm số gần đúng của a = 2851275 với độ chính xác d = 300

A. 2851000.

B. 2851575.

C. 2850025.

D. 2851200

Câu 8: Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001.

A. 5,25.

B. 5,24.

C. 5,246.

D. 5,2

Câu 9: Sử dụng mãy tính bỏ túi, hãy viết giá trị gần đúng của $\sqrt{3}$ chính xác đến hàng phần trăm

A. 1,73.

B. 1,732.

C. 1,7.

D. 1,7320

Câu 10: Sử dụng mãy tính bỏ túi, hãy viết giá trị gần đúng của ${\pi }^2$ chính xác đến hàng phần nghìn.

A. 9,870.

B. 9,869.

C. 9,871.

D. 9,8696

Câu 11: Hãy viết số quy tròn của số $a$ với độ chính xác $d$ được cho sau đây:

$\overline{a}$ = 17658 $\pm$ 16.

A. 17700.

B. 17660.

C. 18000.

D. 17674

DẠNG 4: XÁC ĐỊNH CÁC CHỮ SỐ CHẮC CỦA MỘT SỐ GẦN ĐÚNG, DẠNG CHUẨN CỦA CHỮ SỐ GẦN ĐÚNG VÀ KÍ HIỆU KHOA HỌC CỦA MỘT SỐ.

Câu 12: Tìm số chắc của số gần đúng a biết số người dân tỉnh Nghệ An là $a=3214056$ người với độ chính xác $d=100$ người.

A. 1,2,3,4.

B. 1,2,3,4,0.

C. 1,2,3.

D. 1,2,3,4,0,5.

Câu 13: Viết dạng chuẩn của số gần đúng a biết số người dân tỉnh Nghệ An là $a=3214056$ người với độ chính xác $d=100$ người.

A. .

B. .

C. .

D.

Câu 14: Viết dạng chuẩn của số gần đúng a biết $a=1,3462$ sai số tương đối của a bằng 1%.

A. 1,3.

B. 1,34.

C. 1,35.

D. 1,346

Câu 15: Một hình chữ nhật cố diện tích là S = $180,57{cm}^2\pm 0,6{cm}^2$. Kết quả gần đúng của S viết dưới dạng chuẩn là:

A. $180,58c{m}^2$

B. $180,59c{m}^2$

C. $0,181c{m}^2$

D. $181c{m}^2$

BÀI 2. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM
CHO MẪU SỐ LIỆU KHÔNG GHÉP NHÓM

I. SỐ TRUNG BÌNH CỘNG

1. Định nghĩa

Số trung bình (số trung bình cộng) của mẫu số liệu $x_1,x_2,\mathrm{...},x_n$, kí hiệu là $\overline{x}$ , được tính bằng công thức:

$\overline{x}=\frac{x_1+x_2+\mathrm{...}+x_n}{n}$

Chú ý: Trong trường hợp mẫu số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức:

$\overline{x}=\frac{m_1{x}_1+m_2{x}_2+\mathrm{...}+m_k{x}_k}{n}$

Trong đó $m_k$ là tần số của giá trị $x_k$ và $n=m_1+m_2+\mathrm{...}+m_k$.

2. Ý nghĩa.

Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để dại diện cho mẫu số liệu.

II. TRUNG VỊ

1. Định nghĩa

Để tìm trung vị của một mẫu số liệu, ta thực hiện như sau:

+ Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

2. Ý nghĩa.

Trung vị là giá trị chia đôi mẫu số liệu, nghĩa là trong mẫu số liệu được sắp xếp theo thứ tự không giảm thì giá trị trung vị ở vị trí chính giữa. Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường.

III. TỨ PHÂN VỊ

1. Định nghĩa

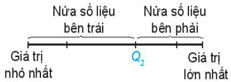
Hình 5.3b

Chú ý: $Q_1$ được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, $Q_3$ được gọi là tứ phân vị thứ ba hay tứ phân vị trên.

2. Ý nghĩa. Các điểm $Q_1,Q_2,Q_3$ chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa $25\%$ giá trị (hình 5.3a).

Hình 5.3a. Các tứ phân vị

VÍ DỤ: Hàm lượng Natri (đơn vị miligam, $1mg=0,001g$) trong 100g một số loại ngũ cốc được cho như sau:

Hãy tìm các tứ phân vị. Các phân vị này cho ta thông tin gì?

Giải

- Sắp xếp các giá trị này theo thứ tự không giảm:

- Vì $n=20$ là số chẵn nên $Q_2$ là trung bình cộng của hai giá trị chính giữa:

$Q_2=\left(180+180\right):2=180$

- Ta tìm $Q_1$ là trung vị của nửa số liệu bên trái $Q_2$:

$05070100\underset{}{\underbrace{130140}}140150160180$

và ta tìm được $Q_1=\left(130+140\right):2=135$.

- Ta tìm $Q_3$ là trung vị của nửa số liệu bên phải $Q_2$:

$180180190200\underset{}{\underbrace{200210}}210220290340$

và tìm được $Q_3=\left(200+210\right):2=205$.

Hình 5.4. Hình ảnh về sự phân bố của mẫu số liệu

Các tứ phân vị cho ta hình ảnh phân bố của mẫu số liệu. Khoảng cách từ $Q_1$ đến $Q_2$ là 45 trong khi khoảng cách từ $Q_2$ đến $Q_3$ là 25. Điều này cho thấy mẫu số liệu tập trung mật độ cao ở bên phải $Q_2$ và mật độ thấp ở bên trái $Q_2$ (H.5.4).

IV. MỐT

1. Định nghĩa

Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.

2. Ý nghĩa

Có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.

Câu 1. Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

b) Giá của một số loại giày (đơn vị nghìn đồng):

c) Số kênh được chiếu của một số hãng truyền hình cáp:

Câu 2.Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tính giá trị của số đặc trưng đó.

a) Số mặt trăng đã biết của các hành tinh:

(Theo NASA)

b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

Xem thêm chuyên đề dạy thêm Toán 10 hay, chi tiết khác:

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Chuyên đề Hàm số và đồ thị

Chuyên đề Hệ thức lượng trong tam giác. Vectơ

Chuyên đề Một số yếu tố thống kê và xác suất

Chuyên đề Phương pháp tọa độ trong mặt phẳng