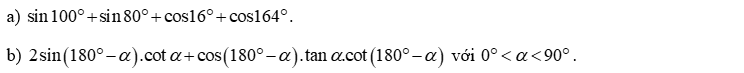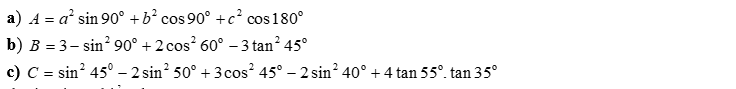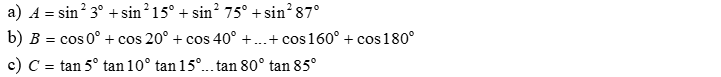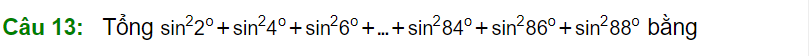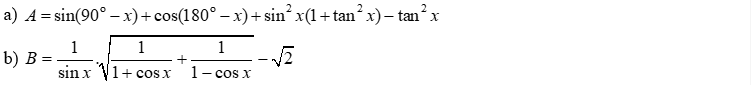Chuyên đề Hệ thức lượng trong tam giác. Vectơ lớp 10 (Cánh diều) | Chuyên đề dạy thêm Toán 10

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 10 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐỘ ĐẾN 180 ĐỘ .

I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ ĐẾN .

1. Định nghĩa.

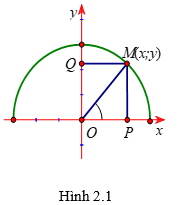
Trong mặt phẳng tọa độ $Oxy$. Với góc $\alpha \left(0^{\text{o}}\le \alpha \le {180}^{\text{o}}\right)$ , ta xác định được duy nhất điểm $M$ trên trên đường nửa đường tròn đơn vị tâm $O$, sao cho $\alpha =\widehat{xOM}$, biết $M\left(x;y\right)$ .

Khi đó:

$\sin \alpha =y;\cos \alpha =x;$

$\tan \alpha =\frac{y}{x}(\alpha \ne {90}^{\text{o}});$

$\cot \alpha =\frac{x}{y}(\alpha \ne 0^{\text{o}},{180}^{\text{o}})$

Các số $\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \beta$ được gọi là giá trị lượng giác của góc .

Chú ý: Với $0^{\text{o}}\le \alpha \le {180}^{\text{o}}$. ta có:

$0\le \sin \alpha \le 1;-1\le \cos \alpha \le 1$

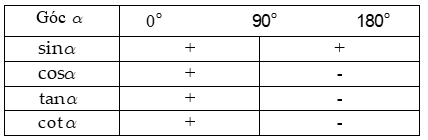
2. Dấu của giá trị lượng giác.

3. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

$\begin{array}{c}\sin ({180}^{\text{o}}-\alpha )=\sin \alpha \\ \cos ({180}^{\text{o}}-\alpha )=-\cos \alpha \\ \tan ({180}^{\text{o}}-\alpha )=-\tan \alpha \\ \cot ({180}^{\text{o}}-\alpha )=-\cot \alpha \end{array}$

4. Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau (bổ sung)

$\begin{array}{c}\sin ({90}^{\text{o}}-\alpha )=\cos \alpha \\ \cos ({90}^{\text{o}}-\alpha )=\sin \alpha \\ \tan ({90}^{\text{o}}-\alpha )=\cot \alpha \\ \cot ({90}^{\text{o}}-\alpha )=\tan \alpha \end{array}$

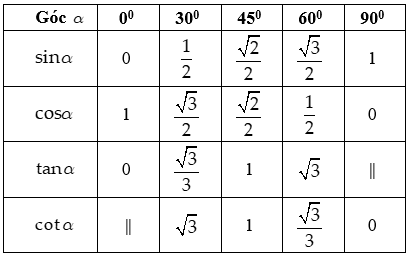
5. Giá trị lượng giác của các góc đặc biệt

6. Các hệ thức lượng giác cơ bản (bổ sung – kết quả của bài tập)

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }(\alpha \ne {90}^{\text{o}})$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }(\alpha \ne 0^{\text{o}};{180}^{\text{o}})$

$\tan \alpha .\cot \alpha =1(\alpha \ne 0^{\text{o}};{90}^{\text{o}};{180}^{\text{o}})$

${\sin }^2\alpha +{\cos }^2\alpha =1$

$1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }(\alpha \ne {90}^{\text{o}})$

$c{\mathrm{ot}}^2\alpha =\frac{1}{{\sin }^2\alpha }(\alpha \ne 0^{\text{o}};{180}^{\text{o}})$

Câu 1. Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:

Câu 2. Đơn giản biểu thức sau:

Câu 3. Chứng minh các hệ thức sau:

a) ${\sin }^2\alpha +{\text{cos}}^2\alpha =1$;

b) $1+{\tan }^2\alpha =\frac{1}{{\text{cos}}^2\alpha }\left(\alpha \ne 90°\right);$

c) $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(0°<\alpha <180°\right);$

Câu 4. Cho góc $\alpha \left(0°<\alpha <180°\right)$ thỏa mãn $\tan \alpha =3$.

Tính giá trị của biểu thức $P=\frac{2\sin \alpha -3\text{cos}\alpha }{3\sin \alpha +2\text{cos}\alpha }$ .

DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC

- Sử dụng định nghĩa giá trị lượng giác của một góc

- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt

- Sử dụng các hệ thức lượng giác cơ bản

Câu 1. Tính giá trị các biểu thức sau:

Câu 2. Tính giá trị các biểu thức sau:

Câu 1: Giá trị của $\cos {60}^{\text{o}}+\sin {30}^{\text{o}}$ bằng bao nhiêu?

A. $\frac{\sqrt{3}}{2}$

B. $\sqrt{3}$

C. $\frac{\sqrt{3}}{3}$

D. $1$

Câu 2: Giá trị của $\tan {30}^{\text{o}}+\cot {30}^{\text{o}}$ bằng bao nhiêu?

A. $\frac{4}{\sqrt{3}}$

B. $\frac{1+\sqrt{3}}{3}$

C. $\frac{2}{\sqrt{3}}$

D. $2$

Câu 3: Trong các đẳng thức sau đây, đẳng thức nào sai?

A. $\sin 0^{\text{o}}+\cos 0^{\text{o}}=1$

B. $\sin {90}^{\text{o}}+\cos {90}^{\text{o}}=1$

C. $\sin {180}^{\text{o}}+\cos {180}^{\text{o}}=-1$

D. $\sin {60}^{\text{o}}+\cos {60}^{\text{o}}=1$

Câu 4: Trong các khẳng định sau, khẳng định nào sai?

A. $\cos {60}^{\text{o}}=\sin {30}^{\text{o}}$

B. $\cos {60}^{\text{o}}=\sin {120}^{\text{o}}$

C. $\cos {30}^{\text{o}}=\sin {120}^{\text{o}}$

D. $\sin {60}^{\text{o}}=-\cos {120}^{\text{o}}$

Câu 5: Đẳng thức nào sau đây sai?

A. $\sin {45}^{\text{o}}+\sin {45}^{\text{o}}=\sqrt{2}$

B. $\sin {30}^{\text{o}}+\cos {60}^{\text{o}}=1$

C. $\sin {60}^{\text{o}}+\cos {150}^{\text{o}}=0$

D. $\sin {120}^{\text{o}}+\cos {30}^{\text{o}}=0$

Câu 6: Giá trị $\cos {45}^{\text{o}}+\sin {45}^{\text{o}}$ bằng bao nhiêu?

A. $1$

B. $\sqrt{2}$

C. $\sqrt{3}$

D. $0$

Câu 7: Trong các đẳng thức sau, đẳng thức nào đúng?

A. $\sin \left({180}^{\text{o}}-\alpha \right)=-\cos \alpha$

B. $\sin \left({180}^{\text{o}}-\alpha \right)=-\sin \alpha$

C. $\sin \left({180}^{\text{o}}-\alpha \right)=\sin \alpha$

D. $\sin \left({180}^{\text{o}}-\alpha \right)=\cos \alpha$

Câu 8: Trong các đẳng thức sau, đẳng thức nào sai?

A. $\sin 0^{\text{o}}+\cos 0^{\text{o}}=0$

B. $\sin {90}^{\text{o}}+\cos {90}^{\text{o}}=1$

C. $\sin {180}^{\text{o}}+\cos {180}^{\text{o}}=-1$

D. $\sin {60}^{\text{o}}+\cos {60}^{\text{o}}=\frac{\sqrt{3}+1}{2}$

Câu 9: Cho $x$ là góc tù. Điều khẳng định nào sau đây là đúng?

A. $\sin \alpha <0$

B. $\cos \alpha >0$

C. $\tan \alpha <0$

D. $\cot \alpha >0$

Câu 10: Giá trị của

$E=\sin {36}^{\text{o}}\cos 6^{\text{o}}\sin {126}^{\text{o}}\cos {84}^{\text{o}}$ là

A. $\frac{1}{2}$

B. $\frac{\sqrt{3}}{2}$

C. $1$

D. $-1$

Câu 11: Giá trị của biểu thức:

$A={\sin }^2{51}^{\text{o}}+{\sin }^2{55}^{\text{o}}+{\sin }^2{39}^{\text{o}}+{\sin }^2{35}^{\text{o}}$ là:

A. 3

B. 4

C. 1

D. 2

Câu 12: Giá trị của biểu thức:

$A=\tan 1^{\text{o}}\tan 2^{\text{o}}\tan 3^{\text{o}}\mathrm{...}\tan {88}^{\text{o}}\tan {89}^{\text{o}}$ là:

A. 0

B. 2

C. 3

D. 1

A. 21

B. 23

C. 22

D. 24

Câu 14: Giá trị của

$A=\tan 5^{\text{o}}.\tan {10}^{\text{o}}.\tan {15}^{\text{o}}\mathrm{...}\tan {80}^{\text{o}}.\tan {85}^{\text{o}}$ là:

A. 2

B. 1

C. 0

D. -1

Câu 15: Giá trị của

$B={\cos }^2{73}^{°}+{\cos }^2{87}^{°}+{\cos }^2{3}^{°}+{\cos }^2{17}^{°}$ là

A. $\sqrt{2}$

B. $2$

C. $-2$

D. $1$

DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC, KHI BIẾT TRƯỚC MỘT GIÁ TRỊ LƯỢNG GIÁC.

- Dựa vào các hệ thức lượng giác cơ bản

- Dựa vào dấu của giá trị lượng giác

- Sử dụng các hằng đẳng thức đáng nhớ

Câu 1. Cho $\sin \alpha =\frac{1}{3}$ với ${90}^0<\alpha <{180}^0$. Tính $\cos \alpha$ và $\tan \alpha$

Câu 2. Cho $\cos \alpha =-\frac{2}{3}$ và $\sin \alpha >0$. Tính $\sin \alpha$ và $\cot \alpha$

Câu 3. Cho $\tan \gamma =-2\sqrt{2}$ tính giá trị lượng giác còn lại.

Câu 4. Cho $\cos \alpha =\frac{3}{4}$ với $0^0<\alpha <{90}^0$.

Tính $A=\frac{\tan \alpha +3\cot \alpha }{\tan \alpha +\cot \alpha }$.

Câu 5. Cho $\tan \alpha =\sqrt{2}$.

Tính $B=\frac{\sin \alpha -\cos \alpha }{{\sin }^3\alpha +3{\cos }^3\alpha +2\sin \alpha }$

Câu 6. Biết $\sin x+\cos x=m$

a) Tìm $|{\sin }^{4}x-{\cos }^{4}x|$.

b) Chứng minh rằng $\left|m\right|\le \sqrt{2}$.

Câu 1: Cho $\cos x=\frac{1}{2}$.

Tính biểu thức $P=3{\sin }^{2}x+4{\cos }^{2}x$

A. $\frac{13}{4}$

B. $\frac{7}{4}$

C. $\frac{11}{4}$

D. $\frac{15}{4}$

Câu 2: Biết .$\cos \alpha =\frac{1}{3}$ Giá trị đúng của biểu thức $P={\sin }^2\alpha +3{\cos }^2\alpha$ là:

A. $\frac{1}{3}$

B. $\frac{10}{9}$

C. $\frac{11}{9}$

D. $\frac{4}{3}$

Câu 3: Cho biết $\tan \alpha =\frac{1}{2}$. Tính $\cot \alpha$.

A. $\cot \alpha =2$.

B. $\cot \alpha =\sqrt{2}$.

C. $\cot \alpha =\frac{1}{4}$.

D. $\cot \alpha =\frac{1}{2}$

Câu 4: Cho biết $\cos \alpha =-\frac{2}{3}$ và $0<\alpha <\frac{\pi }{2}$. Tính $\tan \alpha$?

A. $\frac{5}{4}$ .

B. $-\frac{5}{2}$ .

C. $\frac{\sqrt{5}}{2}$ .

D. $-\frac{\sqrt{5}}{2}$ .

Câu 5: Cho $\alpha$ là góc tù và $\sin \alpha =\frac{5}{13}$. Giá trị của biểu thức $3\sin \alpha +2\cos \alpha$ là

A. $3$

B. $-\frac{9}{13}$

C. $-3$

D. $\frac{9}{13}$

Câu 6: Cho biết $\sin \alpha +\cos \alpha =a$. Giá trị của $\sin \alpha .\cos \alpha$ bằng bao nhiêu?

A. $\sin \alpha .\cos \alpha =a^2$

B. $\sin \alpha .\cos \alpha =2a$

C. $\sin \alpha .\cos \alpha =\frac{1-a^2}{2}$

D. $\sin \alpha .\cos \alpha =\frac{a^2-1}{2}$

Câu 7: Cho biết $\cos \alpha =-\frac{2}{3}$. Tính giá trị của biểu thức $E=\frac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$ ?

A. $-\frac{19}{13}$

B. $\frac{19}{13}$

C. $\frac{25}{13}$

D. $-\frac{25}{13}$

Câu 8: Cho biết $\cot \alpha =5$. Tính giá trị của $E=2{\cos }^2\alpha +5\sin \alpha \cos \alpha +1$ ?

A. $\frac{10}{26}$ .

B. $\frac{100}{26}$ .

C. $\frac{50}{26}$ .

D. $\frac{101}{26}$ .

Câu 9: Cho $\cot \alpha =\frac{1}{3}$. Giá trị của biểu thức $A=\frac{3\sin \alpha +4\cos \alpha }{2\sin \alpha -5\cos \alpha }$ là:

A. $-\frac{15}{13}$

B. $-13$

C. $\frac{15}{13}$

D. $13$

Câu 10: Cho biết $\cos \alpha =-\frac{2}{3}$. Giá trị của biểu thức $E=\frac{\cot \alpha -3\tan \alpha }{2\cot \alpha -\tan \alpha }$ bằng bao nhiêu?

A. $-\frac{25}{3}$

B. $-\frac{11}{13}$

C. $-\frac{11}{3}$

D. $-\frac{25}{13}$

Câu 11: Biết $\sin a+\cos a=\sqrt{2}$. Hỏi giá trị của ${\sin }^{4}a+{\cos }^{4}a$ bằng bao nhiêu?

A. $\frac{3}{2}$

B. $\frac{1}{2}$

C. $-1$

D. $0$

Câu 12: Cho $\tan \alpha +\cot \alpha =m$. Tìm $m$ để ${\tan }^2\alpha +{\cot }^2\alpha =7$.

A. $m=9$

B. $m=3$

C. $m=-3$

D. $m=\pm 3$

Câu 13: Cho biết $3\cos \alpha -\sin \alpha =1$, $0^{\text{o}}<\alpha <{90}^{\text{o}}$. Giá trị của $\tan \alpha$ bằng

A. $\tan \alpha =\frac{4}{3}$

B. $\tan \alpha =\frac{3}{4}$

C. $\tan \alpha =\frac{4}{5}$

D. $\tan \alpha =\frac{5}{4}$

Câu 14: Cho biết $2\cos \alpha +\sqrt{2}\sin \alpha =2$, $0^0<\alpha <{90}^0.$ Tính giá trị của $\cot \alpha .$

A. $\cot \alpha =\frac{\sqrt{5}}{4}$

B. $\cot \alpha =\frac{\sqrt{3}}{4}$

C. $\cot \alpha =\frac{\sqrt{2}}{4}$

D. $\cot \alpha =\frac{\sqrt{2}}{2}$

Câu 15: Cho biết $\cos \alpha +\sin \alpha =\frac{1}{3}.$ Giá trị của $P=\sqrt{{\tan }^2\alpha +{\cot }^2\alpha }$ bằng bao nhiêu?

A. $P=\frac{5}{4}$

B. $P=\frac{7}{4}$

C. $P=\frac{9}{4}$

D. $P=\frac{11}{4}$

Câu 16: Cho biết $\sin \alpha -\cos \alpha =\frac{1}{\sqrt{5}}.$ Giá trị của $P=\sqrt{{\sin }^4\alpha +{\cos }^4\alpha }$ bằng bao nhiêu?

A. $P=\frac{\sqrt{15}}{5}$

B. $P=\frac{\sqrt{17}}{5}$

C. $P=\frac{\sqrt{19}}{5}$

D. $P=\frac{\sqrt{21}}{5}$

DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC

- Sử dụng các hệ thức lượng giác cơ bản

- Sử dụng tính chất của giá trị lượng giác

- Sử dụng các hằng đẳng thức đáng nhớ .

Câu 1. Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa)

a) ${\sin }^{4}x+{\cos }^{4}x=1-2{\sin }^{2}x.{\cos }^{2}x$

b) $\frac{1+\cot x}{1-\cot x}=\frac{\tan x+1}{\tan x-1}$

c) $\frac{\cos x+\sin x}{{\cos }^{3}x}={\tan }^{3}x+{\tan }^{2}x+\tan x+1$

Câu 2. Cho tam giác $ABC$. Chứng minh:

$\frac{{\sin }^3\frac{B}{2}}{\cos \left(\frac{A+C}{2}\right)}+\frac{{\cos }^3\frac{B}{2}}{\sin \left(\frac{A+C}{2}\right)}-\frac{\cos \left(A+C\right)}{\sin B}.\tan B=2$

Câu 3. Đơn giản các biểu thức sau (giả sử các biểu thức sau đều có nghĩa)

Câu 4. Chứng minh biểu thức sau không phụ thuộc vào $x$.

Câu 1: Trong các hệ thức sau hệ thức nào đúng?

A. ${\sin }^2\alpha +\cos {\alpha }^2=1$

B. ${\sin }^2\alpha +{\cos }^2\frac{\alpha }{2}=1$

C. $\sin {\alpha }^2+\cos {\alpha }^2=1$

D. ${\sin }^{2}2\alpha +{\cos }^{2}2\alpha =1$

................................

................................

................................

Xem thử tài liệu tại đây: Link tài liệu

Xem thêm chuyên đề dạy thêm Toán 10 hay, chi tiết khác:

Chuyên đề Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Chuyên đề Hàm số và đồ thị

Chuyên đề Đại số tổ hợp

Chuyên đề Một số yếu tố thống kê và xác suất

Chuyên đề Phương pháp tọa độ trong mặt phẳng