Chứng minh rằng: Nếu MN < MP thì HN < HP và góc NMH < góc PMH
Với giải Bài 64 trang 87 sgk Toán 7 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải Toán 7 Ôn tập chương 3
Video giải Bài 64 trang 87 Toán lớp 7 Tập 2
Bài 64 trang 87 Toán lớp 7 Tập 2: Gọi MH là đường cao của tam giác MNP. Chứng minh rằng: Nếu thì và (yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).
Lời giải:
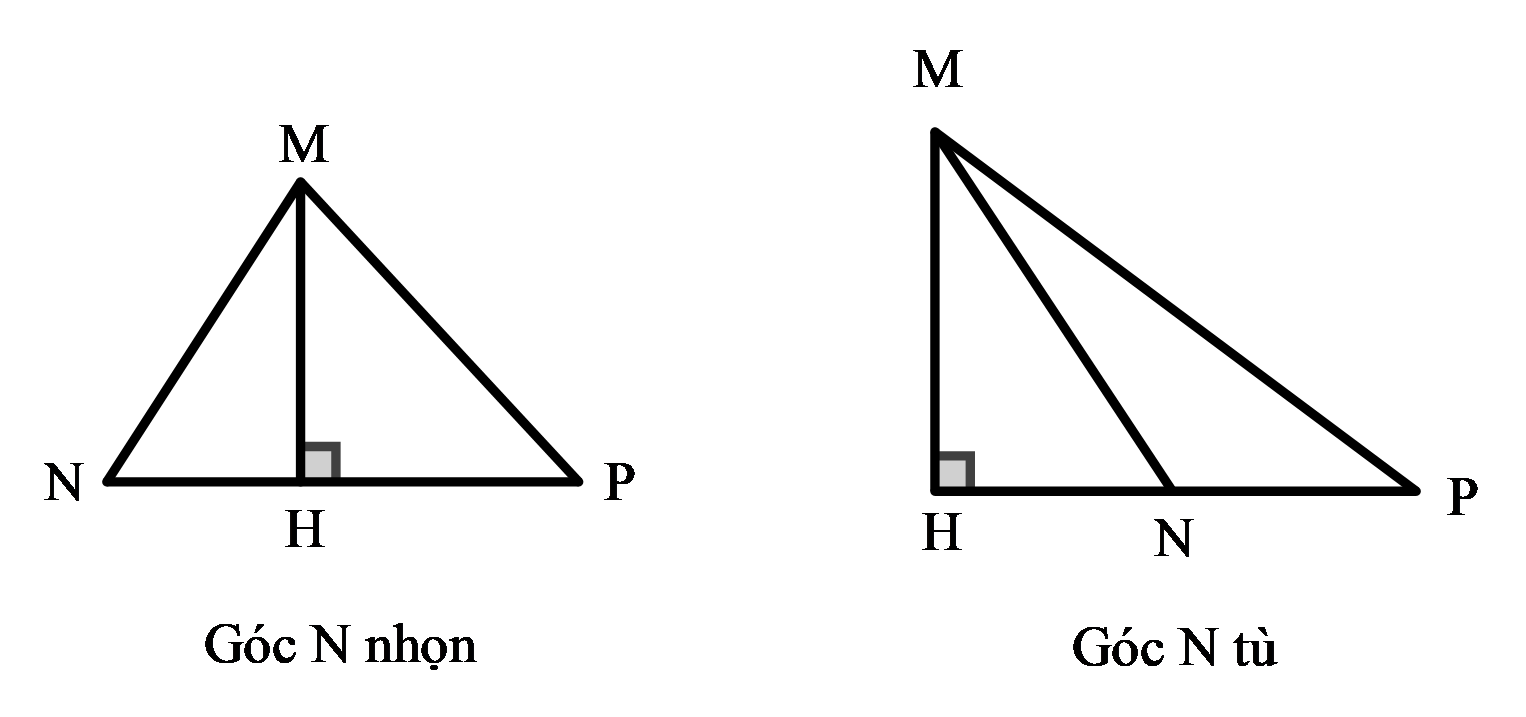
+ So sánh NH và PH.
MH là đường cao của ΔMNP nên H là hình chiếu của M trên đường thẳng NP.
⇒ HN là hình chiếu của đường xiên MN trên đường thẳng NP; HP là hình chiếu của đường xiên MP trên đường thẳng NP.
Mà MN < MP ⇒ HN < HP (quan hệ giữa đường xiên và hình chiếu).
+ So sánh và
TH1: Xét ΔMNP có góc N nhọn.
Vì ΔMNP có góc N nhọn nên suy ra góc P nhọn (vì MN < MP nên ) (1)
ΔMNH vuông tại H có (2)
ΔMPH vuông tại H có (3)
Từ (1), (2) và (3) suy ra
TH2: Xét ΔMNP có góc N tù.
Vì ΔMNP có góc N tù nên suy ra H nằm ngoài cạnh NP.
Lại có HN < HP nên N nằm giữa H và P
⇒ Tia MN ở giữa hai tia MH và MP
nên suy ra .
Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:
Bài 4 trang 86 Toán 7 Tập 2: Hãy ghép hai ý ở hai cột để được khẳng định đúng...
Bài 5 trang 86 Toán 7 Tập 2: Cũng với yêu cầu như ở câu 4...
Bài 67 trang 87 Toán 7 Tập 2: Cho tam giác MNP với trung tuyến MR và trọng tâm Q...
Bài 68 trang 88 Toán 7 Tập 2: Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy...
Xem thêm các chương trình khác: