Câu hỏi:
18/07/2024 194Có bao nhiêu giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số y=|x3−mx2−9x+9m| trên đoạn [-2;2] đạt giá trị nhỏ nhất
A. 3
B. 5
C. 4
D. 6
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Đặt f(x)=x3−mx2−9x+9m
Dễ thấy min[−2;2]|f(x)|≥0
Dấu “=” xảy ra khi và chỉ khi phương trình f(x)=0 có nghiệm x∈[−2;2]
Ta có: f(x)=x2(x−m)−9(x−m)=(x2−9)(x−m)=0⇔[x=3x=−3x=m
Do đó điều kiện cần và đủ để f(x)=0 có nghiệm x∈[−2;2] là m∈[−2;2]
Mà m∈ℤ nên m∈{−2;−1;0;1;2}
Vậy có 5 giá trị nguyên của thỏa mãn yêu cầu bài toán.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng 2a. Thể tích của khối lăng trụ đã cho bằng
Câu 5:
Cho hình lăng trụ đều và một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt đáy của hình lăng trụ. Gọi V1,V2 lần lượt là thể tích khối lăng trụ và khối trụ. Tính V1V2
Câu 7:
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng và . Phương trình tham số của đường thẳng d là
Câu 8:
Cho khối nón có bán kính đáy bằng a, góc giữa đường sinh và mặt đáy bằng 300 . Thể tích khối nón đã cho bằng
Câu 9:
Cho hàm số y=ax4+bx3+cx+d (a,b,c,d∈ℝ;a≠0) có đồ thị như hình vẽ bên dưới
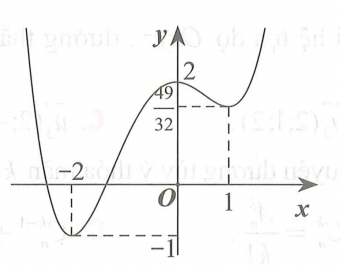
Các điểm cực tiểu của hàm số là
Câu 10:
Trong không gian với hệ tọa độ Oxyz, đường thẳng d:x−12=y−2−1=z−32 có véctơ chỉ phương là
Câu 11:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và góc giữa SC với mặt phẳng (SAB) bằng 30o. Gọi M là điểm di động trên cạnh CD và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh CD thì thể tích của khối chóp S.ABH đạt giá trị lớn nhất bằng
Câu 14:
Cho hàm số y = f(x) có đạo hàm trên và có đồ thị như hình bên. Hàm số g(x)=2f(x+2)+(x+1)(x+3) có bao nhiêu điểm cực tiểu?
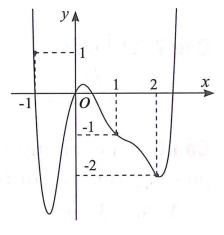
Câu 15:
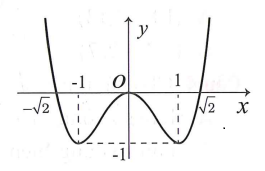
Cho hàm số f(x) nhận giá trị dương trên {0;1], có đạo hàm dương và liên tục trên [0;1], thỏa mãn f(0) = 1 và 1∫0[f3(x)+4[f' Tính



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)