Câu hỏi:
11/11/2024 146Với a là số thực dương, ln(7a)-ln(3a) bằng
B. ln(4a)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải
Ta có:
*Phương pháp giải
Sử dụng công thức 1 thương của logarrit
– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
Logarit của một thương bằng hiệu các logarit.
*Lý thuyết
1. Định nghĩa logarit
Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.
Ví dụ 1.
a) log3 27 = 3 vì 33 = 27.
b) vì .
– Chú ý: Không có logarit của số âm và số 0.
2. Tính chất của logarit
Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:
loga1 = 0; logaa = 1
1. Logarit của một tích
– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
Logarit của một tích bằng tổng các logarit.
Ví dụ 3.
– Chú ý:
Định lí 1 có thể mở rộng cho tích n số dương:
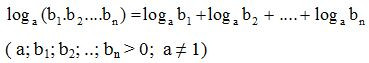
2. Logarit của một thương
– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
Logarit của một thương bằng hiệu các logarit.
Đặc biệt: ( a > 0; b > 0; a ≠ 1)
– Ví dụ 4.
3. Logarit của một lũy thừa
– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:
Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.
– Đặc biệt:
Xem thêm
TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12
Lý thuyết Lôgarit (2024) và bài tập có đáp án
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Kí hiệu là số các tổ hợp chập k của n phần tử, là số các chỉnh hợp chập k của n phần tử. Cho tập X có 2020 phần tử. Số tập con gồm 10 phần tử của tập X bằng
Câu 4:
Cho hàm số y=f(x) có bảng biến thiên như sau.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là
Câu 5:
Cho hàm số y=f(x) có đạo hàm trên và đồ thị hàm số y=f'(x) như hình bên. Khẳng định nào sau đây là đúng?
Câu 6:
Cho dãy số thỏa mãn điều kiện Gọi là tổng của n số hạng đầu tiên của dãy số đã cho. Khi đó bằng
Câu 7:
Cho a và b lần lượt là số hạng thứ nhất và thứ chín của một cấp số cộng có công sai Giá trị của bằng
Câu 8:
Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc. Các điểm M,N,P lần lượt là trung điểm của các đoạn thẳng Biết rằng Thể tích V của khối tứ diện AMNP bằng
Câu 9:
Cho hình hộp ABCD.A'B'C'D' có thể tích V. Gọi M,N,P lần lượt thuộc các cạnh sao cho Thể tích của khối tứ diện tính theo V bằng
Câu 10:
Cho khối chóp tứ giác đều S.ABCD có AB=a. Thể tích khối chóp S.ABCD bằng Khoảng cách từ C đến mặt phẳng (SAB) bằng
Câu 11:
Cho hàm số có đồ thị như hình vẽ
Khẳng định nào dưới đây là đúng?
Câu 12:
Cho hàm số có đồ thị như hình vẽ.
Khi đó phương trình có bao nhiêu nghiệm?
Câu 13:
Số giá trị nguyên của tham số m để hàm số không có điểm cực đại là
Câu 14:
Biết tập nghiệm của bất phương trình là khoảng (a;b). Tổng a+b bằng?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)