Câu hỏi:
19/07/2024 193Từ các chữ số tự nhiên 1, 2, 3 có thể lập được bao nhiêu số khác nhau có những chữ số khác nhau.
A. 15.
B. 6.
C. 3.
D. 12.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Có 3 phương án lựa chọn:
+ Phương án 1: Số có 1 chữ số khác nhau; có 3 cách chọn: 1; 2; 3.
+ Phương án 2: Số có 2 chữ số khác nhau; có 6 cách chọn: 12; 21; 13; 31; 23; 32.
+ Phương án 3: Số có 3 chữ số khác nhau; có 6 cách chọn: 123; 132; 213; 231; 321; 312.
Vậy có 3 + 6 + 6 = 15 cách chọn.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hàm số xác định và liên tục trên , có đạo hàm thỏa mãn
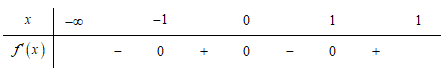
Hàm số nghịch biến trên khoảng nào dưới đây
Câu 3:
Một ô tô đang chạy với vận tốc 20m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc , trong đó là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
Câu 4:
Cho hình chóp có đáy là hình thang vuông tại A và B, , . Đường thẳng vuông góc với mặt phẳng . Gọi E là trung điểm của cạnh SC. Tính khoảng cách d từ điểm E đến mặt phẳng .
Câu 5:
Gọi S là tập hợp tất các các giá trị của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn bằng 3. Tổng tất cả các phần tử của S bằng
Câu 6:
Cho tứ diện ABCD và M, N, P lần lượt thuộc BC, BD, AC sao cho , , . Mặt phẳng cắt AD tại Q. Tính tỷ số thể tích hai phần khối tứ diện ABCD bị chia bởi mặt phẳng .
Câu 7:
Cho hàm số có đồ thị như hình vẽ. Số nghiệm của phương trình là
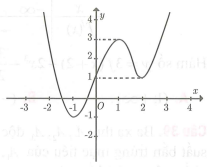
Câu 8:
Ba xạ thủ độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của tương ứng là 0,7; 0,6 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng.
Câu 10:
Cho hàm số có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m sao cho . Số phần tử của tập S là?
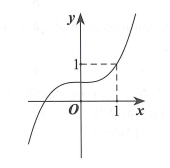
Câu 11:
Gọi là hai nghiệm phức của phương trình . Tính giá trị của biểu thức .
Câu 13:
Trong không gian Oxyz, cho mặt cầu . Xét hai điểm M, N di động trên sao cho . Giá trị nhỏ nhất của bằng
Câu 14:
Cho hàm số có bảng biến thiên như sau:
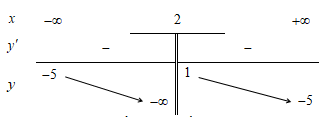
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)