Câu hỏi:
10/10/2024 121
Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
*Phương pháp giải:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
*Lời giải
Xét
Vậy hàm số luôn đồng biến trên --> B
* Một số phương pháp xác định sự đồng biến/nghịch biến của hàm số:
Quy tắc xét sự đơn điệu của hàm số:
- Bước 1. Tìm tập xác định.
- Bước 2. Tính đạo hàm f’(x). Tìm các điểm xi ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Phần I. Các bài toán không chứa tham số.
Dạng 1: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
* Phương pháp giải.
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.
Dạng 2: Từ bảng biến thiên, đồ thị hàm số của hàm số f’(x), xác định khoảng đồng biến, nghịch biến của hàm số đã cho.
* Phương pháp giải.
- Dựa vào bảng biến thiên có sẵn, kết luận khoảng đồng biến, nghịch biến và chọn đáp án đúng.
- Từ đồ thị hàm số của hàm số f’(x), ta có:
+ Khoảng đồng biến của hàm số là khoảng mà tại đó giá trị f'(x) > 0 (nằm phía trên trục hoành).
+ Khoảng đồng biến của hàm số là khoảng mà tại đó f'(x) < 0 (nằm phía dưới trục hoành).
Dạng 3: xét sự đồng biến/nghịch biến của hàm hợp
* Phương pháp giải. Cho hàm y = f(x) hoặc hàm y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x)).
- Tính đạo hàm
- Xét dấu dựa vào dấu của và theo quy tắc nhân dấu. Lưu ý khi xét dấu dựa vào dấu của như sau: Nếu không đổi dấu trên D thì không đổi dấu khi .
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tứ diện ABCD có và tam giác BCD là tam giác vuông tại D. Tính thể tích khối tứ diện ABCD.
Tứ diện ABCD có và tam giác BCD là tam giác vuông tại D. Tính thể tích khối tứ diện ABCD.
Câu 4:
Trong không gian với hệ toạ độ Oxyz. Điểm nào sau đây thuộc mặt phẳng .
Trong không gian với hệ toạ độ Oxyz. Điểm nào sau đây thuộc mặt phẳng .
Câu 8:
Cho hình hộp chữ nhật có ba kích thước là 3cm, 4cm, 5cm. Thể tích của khối hộp chữ nhật là
Cho hình hộp chữ nhật có ba kích thước là 3cm, 4cm, 5cm. Thể tích của khối hộp chữ nhật là
Câu 9:
Cho hàm số y = f(x) có đạo hàm liên tục trên Đồ thị hàm số y = f'(x) như hình bên. Giá trị lớn nhất của hàm số trên đoạn bằng
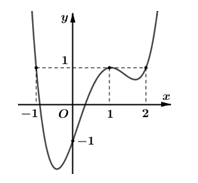
Cho hàm số y = f(x) có đạo hàm liên tục trên Đồ thị hàm số y = f'(x) như hình bên. Giá trị lớn nhất của hàm số trên đoạn bằng

Câu 11:
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của đường thẳng đi qua và vuông góc với mặt phẳng
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của đường thẳng đi qua và vuông góc với mặt phẳng
Câu 12:
Gọi S là tập hợp tất cả các số tự nhiên có 6 chữ số phân biệt được lấy từ các số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ S, xác suất chọn được số chứa đúng 3 chữ số lẻ là
Gọi S là tập hợp tất cả các số tự nhiên có 6 chữ số phân biệt được lấy từ các số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ S, xác suất chọn được số chứa đúng 3 chữ số lẻ là
Câu 13:
Cho hàm số f(x) có bảng biến thiên như sau:
Điểm cực tiểu của hàm số đã cho là:
Câu 14:
Có bao nhiêu giá trị nguyên dương của m < 30 để bất phương trình sau có nghiệm
Có bao nhiêu giá trị nguyên dương của m < 30 để bất phương trình sau có nghiệm
Câu 15:
Cho hình trụ (T)có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu là thể tích khối trụ (T). Công thức nào sau đây là đúng?
Cho hình trụ (T)có chiều cao h, độ dài đường sinh l, bán kính đáy r. Ký hiệu là thể tích khối trụ (T). Công thức nào sau đây là đúng?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)