Câu hỏi:
21/04/2025 16Tính giới hạn: lim[11.2+12.3+...+1n(n+1)]
0
1
32
Không có giới hạn
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B
* Lời giải:
* Phương pháp giải:
Phân tích mỗi phân số thành hiệu của hai phân số đơn giản: 1k(k+1)=1k-1k+1
Viết lại tổng dưới dạng tổng của các hiệu, nhận thấy các số hạng trung gian triệt tiêu.
Tính giới hạn của tổng khi .
* Lý thuyết nắm thêm:
I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Định nghĩa
Định nghĩa 1
Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn K \{x0} và xn → x0, ta có f(xn) → L.
Kí hiệu: limx→∞f(x)=L hay f(x) → L khi x → x0.
Nhận xét: limx→∞x=x0,limx→∞c=c với c là hằng số.
Ví dụ 1. Cho hàm số f(x)=x3−8x−2. Chứng minh rằng limx→2f(x)=12.
Giải
Hàm số xác định trên ℝ\{2}
Giả sử (xn) là một dãy số bất kì, thỏa mãn xn≠2 và xn→2 khi n→+∞.
Ta có:
limf(xn)=limx3n−8xn−2=lim(xn−2)(x2n+2xn+4)xn−2=lim(x2n+2xn+4)=12.
Vậy limx→2f(x)=12.
2. Định lí về giới hạn hữu hạn
Định lí 1
a) Giả sử limx→x0f(x)=L và limx→x0g(x)=M. Khi đó:
limx→x0[f(x)+g(x)]=L+M;limx→x0[f(x)−g(x)]=L−M;limx→x0f(x).g(x)=L.M;limx→x0f(x)g(x)=LM(M≠0);
b) Nếu f(x)≥0 và limx→x0f(x)=L thì L≥0 và limx→x0√f(x)=√L.
(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với x≠x0).
Ví dụ 2. Cho hàm số f(x)=1−x(x−4)2. Tính limx→4f(x).
Giải
Ta có:
limx→4(1−x)=−3<0,
3. Giới hạn một bên
Định nghĩa 2
- Cho hàm số y = f(x) xác định trên (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.
Kí hiệu:
- Cho hàm số y = f(x) xác định trên (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
Kí hiệu: .
Định lí 2
Ví dụ 3. Cho hàm số . Tìm và (nếu có).
Giải
Ta có:
Do đó
Vậy và
II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
Định nghĩa 3
a) Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.
Kí hiệu:
b) Cho hàm số y = f(x) xác định trên (–∞; a).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (xn) bất kì, xn < a và xn → –∞, ta có f(xn) → L.
Kí hiệu:
Chú ý:
a) Với c, k là hằng số và k nguyên dương, ta luôn có:
b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi xn → +∞ hoặc x → –∞
III. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ
1. Giới hạn vô cực
Định nghĩa 4
Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → –∞
Kí hiệu:
Nhận xét:
.
2. Một vài giới hạn đặc biệt
a) với k nguyên dương.
b) Nếu k chẵn thì ;
Nếu k lẻ thì .
3. Một vài quy tắc về giới hạn vô cực
a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương
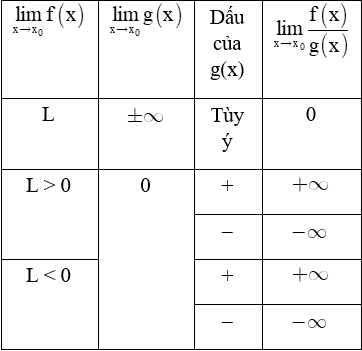
(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với )
Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giới hạn của hàm số (mới 2023 + Bài Tập) – Toán 11
100 bài tập Giới hạn của hàm số (có đáp án 2025) và cách giải
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trên quãng đường AB, dài 210 km, tại cùng một thời điểm một xe máy khởi hành từ A đến B và một ô tô khởi hành từ B đến A. Sau khi gặp nhau, xe máy đi tiếp 4 giờ nữa thì đến B và ô tô đi tiếp 2 giờ 15 phút nữa thì đến A. Biết rằng vận tốc ô tô và xe máy không thay đổi trong suốt chặng đường. Vận tốc của xe máy và ô tô lần lượt là:
Câu 2:
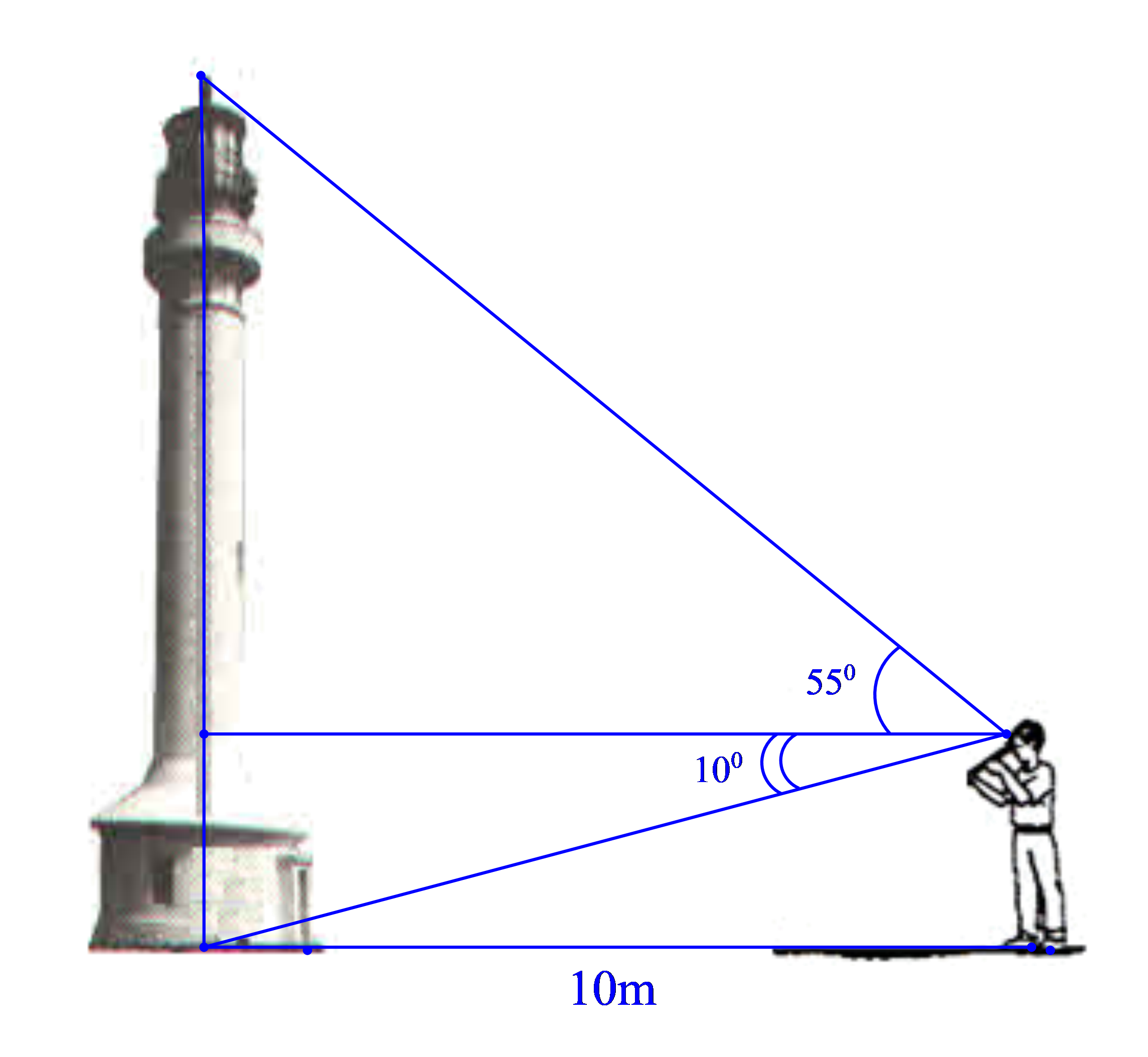
Một người quan sát đứng cách một cái tháp 10m, nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới 1 góc 550 và 100 so với phương ngang của mặt đất. Hãy tính chiều cao của tháp.

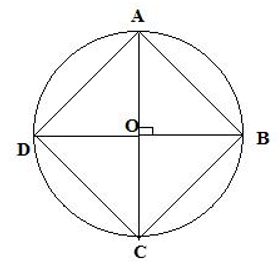
Câu 3:
Trong hình bên, biết diện tích hình vuông là 16m2. Tính diện tích hình tròn tâm O.
Câu 4:
Một ô tô, khối lượng là 4 tấn đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc 10m/s, với công suất của động cơ ô tô là 20kW.
a. Tính hệ số ma sát giữa ô tô và mặt đường.
b. Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường 250m vận tốc ô tô tăng lên đến 54 km/h. Tính công suất trung bình của động cơ ô tô trên quãng đường này và công suất tức thời của động cơ ô tô ở cuối quãng đường. Lấy g = 10m/s2.
Câu 5:
Một tổ công nhân dự định làm xong 240 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện, nhờ cải tiến kĩ thuật nên mỗi ngày tổ đã làm tăng thêm 10 sản phẩm so với dự định. Do đó tổ đã hoàn thành sớm công việc sớm hơn dự định 2 ngày. Hỏi khi thực hiện, mỗi ngày tổ đã làm được bao nhiêu sản phẩm?
Câu 6:
Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác?
Câu 8:
Cho biết mệnh đề nào sau đây là đúng?
a) Hình hộp là hình lăng trụ đứng
b) Hình hộp chữ nhật là hình lăng trụ đứng
c) Hình lăng trụ là hình hộp
d) Có hình lăng trụ không phải là hình hộp
Câu 9:
Cho hình thoi ABCD, góc A = 60. Qua C kẻ đường thẳng d bất kì cắt các tia đối của các tia BA, DA theo thứ tự tại E và F. Gọi I là giao điểm của BF và ED. Chứng minh:
a)
b)
c)
Câu 10:
Cho phương trình log2(2x-1)2 = 2log2(x-2). Số nghiệm thực của phương trình là:
Câu 11:
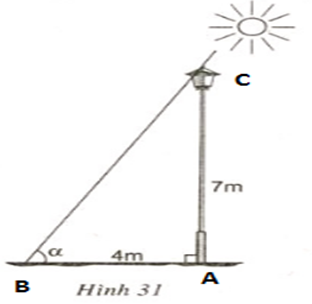
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc α trong hình 31)
Câu 13:
Từ một đài quan sát cao 350m so với mực nước biển, người ta nhìn thấy một chiếc thuyền bị nạn dưới góc 200 so với phương ngang của mực nước biển. Muốn đến cứu con thuyền thì phải đi quãng đường dài bao nhiêu mét?
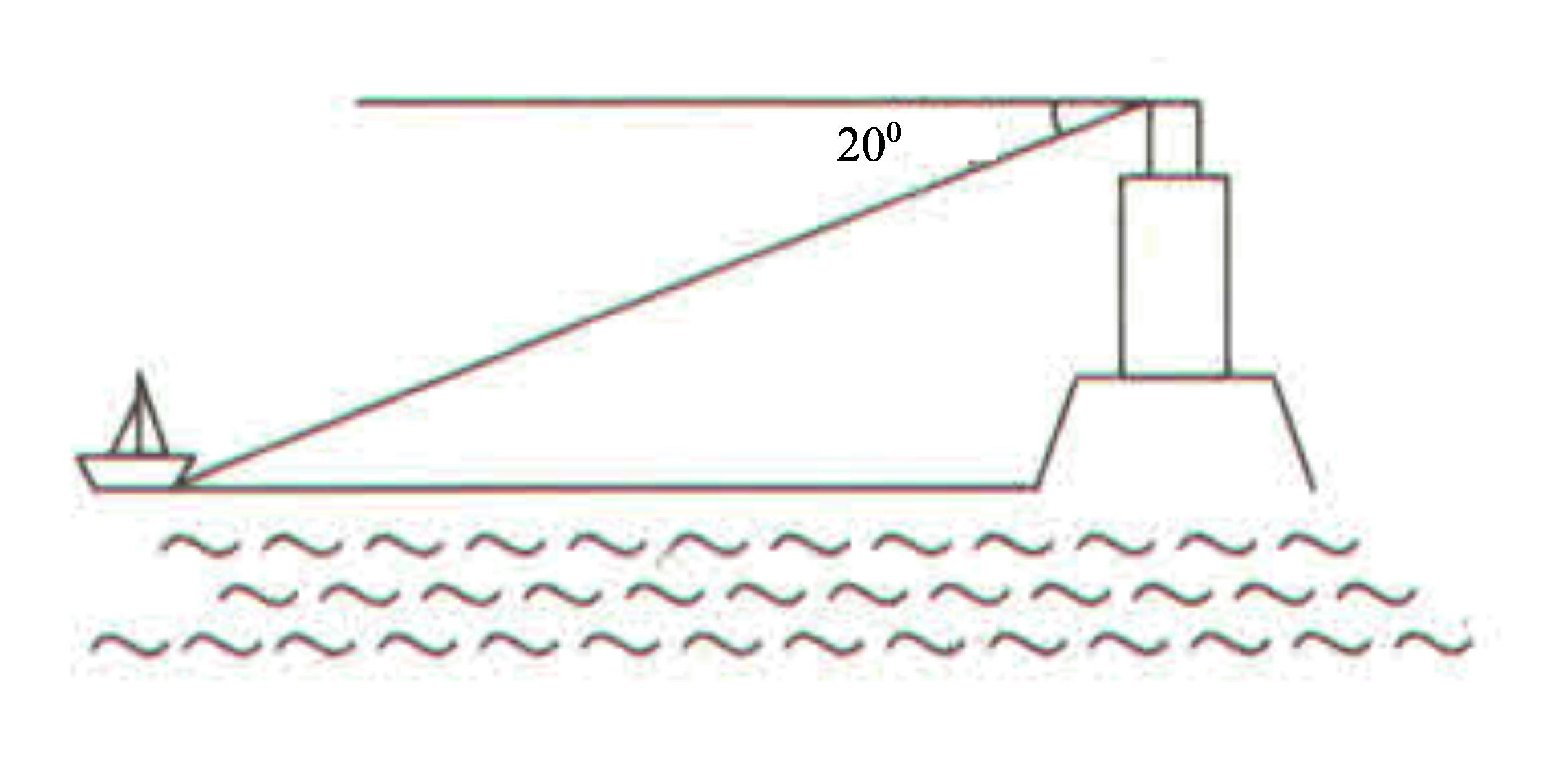

Câu 14:
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ
Câu 15:
Bình có 8 quyển vở, Nguyên có 4 quyển vở. Mai có số vở ít hơn trung bình cộng của cả ba bạn là 2 quyển. Hỏi số vở của Mai là bao nhiêu?