Số nghiệm của phương trình lượng giác: $2\sin x-1=0$ thỏa điều kiện $-\mathrm{\pi }<\mathrm{x}<\mathrm{\pi }$ là

Đáp án đúng: C

*Lời giải

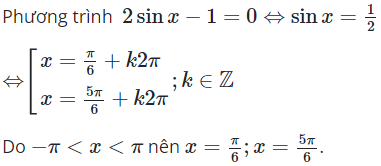
*Phương pháp giải

- đưa về phương trình sinx = a để giải bài toán và tìm nghiệm 

*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:

Phương trình sinx = a (1)

♦ |a| > 1: phương trình (1) vô nghiệm.

♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.

Khi đó phương trình (1) có các nghiệm là

x = α + k2π, k ∈ Z

và x = π-α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 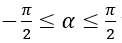 và sinα = a thì ta viết α = arcsin a.

Khi đó các nghiệm của phương trình (1) là

x = arcsina + k2π, k ∈ Z

và x = π - arcsina + k2π, k ∈ Z.

Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x=\frac{\pi }{2}+k2\pi ;k\in Z$.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x=-\frac{\pi }{2}+k2\pi ;k\in Z$.

+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là $x=k\pi ;k\in Z$.

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

at + b = 0 (1)

Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

Phương pháp: Chuyển vế rồi chia hai vế của phương trình (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.

Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.

- Phương pháp:

Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Phương trình lượng giác cơ bản – Toán 11

Toán 11 giải bài tập Bài 2 SGK: Phương trình lượng giác cơ bản

Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Nhận biết)