Câu hỏi:
14/07/2024 117Một sinh viên A trong thời gian 4 năm học đại học đã vay ngân hàng mỗi năm 10 triệu đồng với lãi suất 3%/năm (thủ tục vay một năm một lần vào thời điểm đầu năm học). Khi ra trường A thất nghiệp nên chưa trả được tiền cho ngân hàng do vậy phải chịu lãi suất 8%/năm cho tổng số tiền vay gồm gốc và lãi của 4 năm học. Sau 1 năm thất nghiệp, sinh viên A cũng tìm được việc làm và bắt đầu trả nợ dần. Tổng số tiền mà sinh viên A nợ ngân hàng sau 4 năm học đại học và 1 năm thất nghiệp gần nhất với giá trị nào sau đây ?
A. 43.091.358 đồng
B. 48.621.980 đồng
C. 46.538.667 đồng
D. 45.188.656 đồng
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack

CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, . Cạnh bên SA = vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).
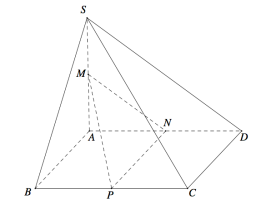
Câu 2:
Cho hình thang cong (H) giới hạn bởi các đường và trục hoành. Đường thẳng x = k ( < k <2) chia (H) thành hai phần có diện tích là và như hình vẽ bên. Tìm tất cả giá trị thực của k để .
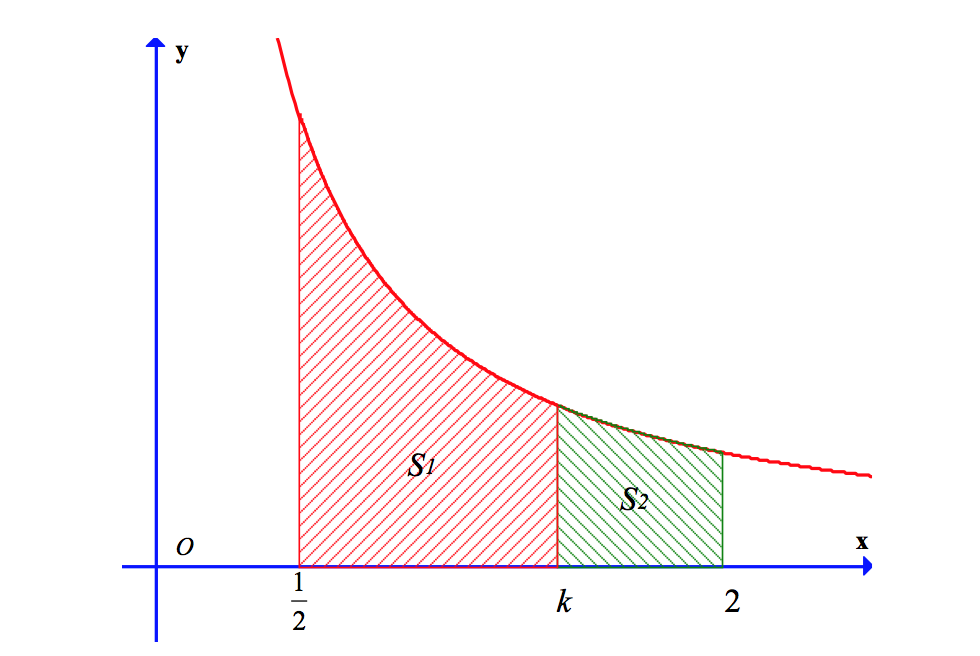
Câu 3:
Một dãy phố có 5 cửa hàng bán quần áo. Có 5 người khách đến mua quần áo, mỗi người khách vào ngẫu nhiên một trong 5 cửa hàng đó. Xác suất để có ít nhất một cửa hàng có nhiều hơn 2 người khách vào bằng
Câu 4:
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x+2y+z-4=0. Có tất cả bao nhiêu mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với ba trục toạ độ x'Ox, y'Oy, z'Oz?
Câu 7:
Cho số phức . Xét các mệnh đề sau :
(1) z là số thực khi và chỉ khi
(2) z là số thuần ảo khi và chỉ khi
(3) z vừa là số thực vừa là số thuần ảo khi và chỉ khi a = 0, b = 0
Số mệnh đề đúng là ?
Câu 8:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên

Có bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)=f(m) có nghiệm thực ?
Câu 9:
Gọi A,B,C lần lượt là điểm biểu diễn của các số phức z, iz và 2z. Biết diện tích tam giác ABC bằng 4. Môđun của số phức z bằng
Câu 10:
Cho hình lập phương ABCD.A′B′C′D′ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AC và BD′ bằng

Câu 11:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1),M(2;4;1),N(1;5;3). Tìm toạ độ điểm C nằm trên mặt phẳng (P):x+z-27=0 sao cho tồn tại các điểm B,D tương ứng thuộc các tia AM, AN để tứ giác ABCD là hình thoi.
Câu 12:
Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;2;1). Tính độ dài đoạn thẳng OA.
Câu 13:
Biết rằng sina, sinacosa, cosa theo thứ tự lập thành một cấp số cộng. Tính S=sina+cosa.
Câu 14:
Trong không gian với hệ toạ độ Oxyz, có bao nhiêu mặt phẳng qua M(-4;-9;12) và cắt các trục toạ độ x'Ox, y'Oy, z'Oz lần lượt tại A(2;0;0),B,C sao cho OB=1+OC.
Câu 15:
Cho số phức z = a+bi thoả mãn là số thuần ảo. Khi số phức z có môđun lớn nhất. Tính giá trị biểu thức P=a+b



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)