Câu hỏi:
19/07/2024 106Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho MNPQ. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN=60cm và thể tích của khối tứ diện MNPQ bằng 30. Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)

A. 101,3
B. 121,3
C. 111,4
D. 141,3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack

CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với A(-1;2;1), B(0;0;-2); C(1;0;1); D(2;1;-1). Tính thể tích tứ diện ABCD?
Câu 2:
Xét các hình chóp S.ABC thỏa mãn SA=a;SB=2a;SC=3a với a là hằng số cho trước. Tìm giá trị lớn nhất của thể tích khối chóp S.ABC?
Câu 4:
Biết đồ thị hàm số có bảng biến thiên như sau:
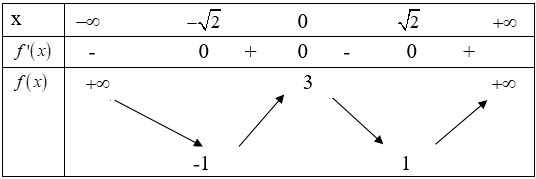
Tìm m để phương trình có đúng 4 nghiệm phân biệt
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-1;1); B(2;1;-2), C(0;0;1) . Gọi H(x;y;z) là trực tâm của tam giác ABC thì giá trị của x+y+z là kết quả nào dưới đây?
Câu 7:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a;AD=2a và AA'=3a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ACB’D’.
Câu 9:
Người ta thiết kế một bể cá bằng kính không có nắp với thể tích 72 và có chiều cao bằng 3 dm. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bể dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
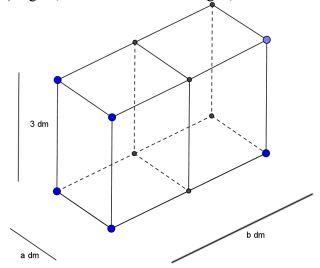
Câu 11:
Dân số thế giới được ước tính theo công thức trong đó A là dân số của năm lấy làm mốc, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm. Theo thống kê dân số thế giới tính đến tháng 01/2017, dân số Việt Nam có 94,970 người và có tỉ lệ tăng dân số là 1,03%. Nếu tỉ lệ tăng dân số không đổi thì đến năm 2020 dân số nước ta có bao nhiêu triệu người, chọn đáp án gần nhất.
Câu 15:
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;2;1); B(3;2;3) , có tâm thuộc mặt phẳng (P):x-y-3=0, đồng thời có bán kính nhỏ nhất, hãy tính bán kính R thuộc mặt cầu (S)?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)