Câu hỏi:
08/10/2024 98Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng
A. 15
B. 9
C. 6
D. 12
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B
*Phương pháp giải:
- Nắm lại kiến thức về hình lập phương: định nghĩa, tính chất, số măt, số đỉnh, số cạnh và các mặt phẳng đối xứng của hình
*Lời giải:
Hình lập phương có tất cả 9 mặt đối xứng gồm:
3 mặt phẳng chia hình lập phương thành 2 khối hộp hình chữ nhật.
6 mặt phẳng chia hình lập phương thành 2 khối lăng trụ tam giác.
*Lý thuyết nắm thêm về hình lập phương:
Công thức thể tích khối lập phương:

*) Dang bài tính thể tích khối lập phương:
+ Dạng 1:Tính thể tích hình lập phương khi biết độ dài một cạnh
* Phương pháp giải: Dựa vào đề bài cho biết độ dài của các cạnh, muốn tính thể tích hình lập phương, ta chỉ cần lấy cạnh nhân với cạnh rồi nhân với cạnh.
+ Dạng 2: Tính thể tích khối lập phương khi đã biết diện tích xung quanh hoặc diện tích toàn phần
* Phương pháp giải: Đầu tiên, ta cần phải tính diện tích 1 mặt rồi mới tìm ra được độ dài cạnh tương ứng. Sau khi đã biết được độ dài cạnh, ta áp dụng công thức thể tích như dạng 1.
+ Dạng 3: Tính độ dài cạnh khi biết được thể tích
* Phương pháp giải: Để tìm một số a chưa biết mà ta có a x a x a = V thì lúc này biết V, ta sẽ dễ dàng tính độ dài cạnh của hình lập phương.
Xem thêm các bài viết liên quan hay, chi tiết:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a,AA' = 2a. Tính khoảng cách giữa hai đường thẳng AB' và A'C
Câu 2:
Cho hình hộp đứng ABCD. có đáy ABCD là hình vuông cạnh a, đường thẳng tạo với mặt phẳng (x ) góc 30°. Tính thể tích khối hộp ABCD.
Câu 3:
Một vật chuyển động theo quy luật với t (giây) là khoảng thời gian từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?
Câu 4:
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
Câu 5:
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'
Câu 6:
Biết đồ thi hàm số y=f(x) có một tiệm cận ngang là y=3. Khi đó đồ thị hàm số y=2f(x)-4 có một tiệm cận ngang là
Câu 8:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn D=[]
Câu 9:
Cho hình chóp S .ABC có SC=2a, SC vuông góc với mặt phẳng (ABC), tam giác ABC đều cạnh 3a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
Câu 10:
Cho hàm số . Tìm tất cả các giá trị thực của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ Olàm trực tâm
Câu 11:
Hỏi hàm số nào có đồ thị là đường cong có dạng như hình vẽ sau đây
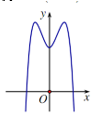
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=2a,BC=a . Các cạnh bên của hình chóp cùng bằng a. Tính góc giữa hai đường thẳngAB và SC
Câu 15:
Hệ số góc tiếp tuyến của đồ thị hàm số tại điểm có tung độ y= -1 là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)