Gọi $m_0$  là số nguyên để phương trình ${\log }_3\left(\frac{x^2}{2020-m}\right)+\left|x\right|\left(x^2+m\right)=2020\left|x\right|$ ,

có hai nghiệm phân biệt $x_1,x_2$  thỏa mãn $x_1^{2020}+x_2^{2020}=2^{1011}$ . Với $m_0$  đó giá trị của biểu thức $P=\ln \left(x_1+\sqrt{x_2^2+2}\right)+\ln \left(x_2+\sqrt{x_1^2+2}\right)$  thuộc vào khoảng nào dưới đây?

 

Có bao nhiêu số tự nhiên có 4 chữ số khác nhau, chia hết cho 4, nhỏ hơn 4567 và có chữ số hàng chục là chữ số lẻ?

Trong không gian Oxyz, cho mặt phẳng $\left(P\right):x+y-z+2=0$  và các điểm $A\left(1;1;1\right),B\left(2;3;1\right)$ . Mặt cầu (S) thay đổi qua A, B và tiếp xúc với (P) tại C. Biết rằng C luôn chạy trên một đường tròn cố định. Diện tích S đường tròn đó bằng

Cho các số thực dương x, y thỏa mãn ${\log }_{4}x={\log }_{9}y={\log }_6\left(\frac{xy}{4}+1\right)$ . Giá trị của biểu thức $P=x^{{\log }_{4}6}+y^{{\log }_{9}6}$  bằng

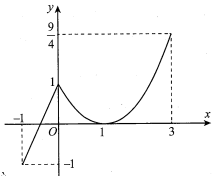
Cho hàm số y=f(x) liên tục trên đoạn $\left[-1;3\right]$  và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn $\left[-1;3\right]$ . Giá trị của $4M-m$  bằng

Một hình trụ có diện tích xung quanh bằng 24π, diện tích toàn phần bằng 42π. Thể tích khối trụ là

Cho hàm số f(x) có đạo hàm liên tục trên $\left[-1;1\right]$ và thỏa mãn f(1)=0,$\left(f^{\text{'}}{\left(x\right)}^2+4f\left(x\right)\right)=8{\text{x}}^2+16\text{x}-8$ với mọi x thuộc $\left[-1;1\right]$ . Giá trị của $\underset{0}{\overset{1}{\int }}f\left(x\right)dx$  bằng

Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BB',A'C'. Thể tích của khối tứ diện CMNP bằng

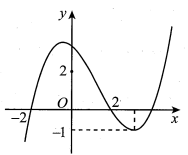
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình $\left|f\left(x^3-3\text{x}\right)\right|=\frac{m+1}{10-m}$  có 10 nghiệm phân biệt?

Họ nguyên hàm của hàm số $f\left(x\right)=\frac{1}{x+1}$  là

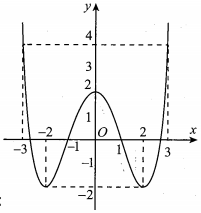
Cho hàm số y=f(x) là hàm bậc bốn trùng phương có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

Cho hàm số y=f(x), y=g(x). Hai hàm số y=f '(x) và y=g'(x) có đồ thị như hình sau. Trong đó đường cong đậm hơn là đồ thị của hàm số y=g'(x) .

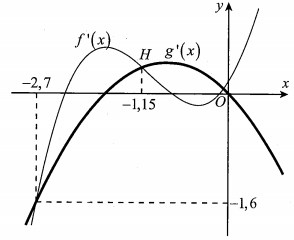
Hàm số $h\left(x\right)=f\left(x\right)-g\left(x\right)$  nghịch biến trên khoảng nào trong các khoảng sau đây?

Trong không gian Oxyz, cho mặt cầu $\left(S\right):{\left(x-1\right)}^2+{\left(y-2\right)}^2+{\left(z-3\right)}^2=9$  và mặt phẳng $\left(P\right):2\text{x}-2y+z+3=0$ . Gọi $M\left(a;b;c\right)$  là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nahát. Khẳng định nào sau đây đúng?

Cho tam giác ABC vuông tại A với AB=a,AC=2a quay xung quanh cạnh AB ta được một khối nón tròn xoay có đường kính l   bằng bao nhiêu?

Cho $m={\log }_a\sqrt{ab}$  với $a,b>1$  và $P=1010{\log }_a^{2}b+2020{\log }_{b}a$ . Khi đó giá trị của m để P đạt giá trị nhỏ nhất là

Cho hàm số $f\left(x\right)=a\sin x+b\cos x$  (với $a,b\in ℝ;b>0$ ), có $f^{\text{'}}\left(0\right)=1$ . Gọi hình phẳng (H) giới hạn bởi đồ thị hàm số f(x) với các trục hoành, trục tung và đường thẳng $x=\pi$ . Khi quay (H) quanh trục Ox thì ta được một vật thể tròn xoay có thể tích bằng $\frac{17{\pi }^2}{2}$ . Khi đó giá trị biểu thức $T=2021\text{a}+b^{10}$  thuộc khoảng nào sau đây?