Giá trị lớn nhất của hàm số $y=x\left(2-\ln x\right)$ trên đoạn $\left[2;3\right]$là

Tính đạo hàm của hàm số sau: $f\left(x\right)=\ln \left(x^2+1\right)$

Cho phương trình:

$(m -1){\log }_{\frac{1}{2}}^2{\left(x-2\right)}^2+4\left(m-5\right){\log }_{\frac{1}{2}}\frac{1}{x-2}+4m-4=0$ (với m là tham số). Gọi $S= [a;b]$ là tập các giá trị của m để phương trình có nghiệm trên đoạn $\left[\frac{5}{2};4\right]$. Tính a+b.

Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Đường sinh của hình trụ (như hình vẽ).

Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là $\frac{128\pi }{3}\left(m^3\right)$.Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị

Cho a, b, c là ba số thực dương, khác 1 và $abc\ne 1$. Biết ${\log }_{a}3=2,{\log }_{b}3=\frac{1}{4}$và ${\log }_{abc}3=\frac{2}{15}.$ Khi đó, giá trị của ${\log }_{c}3$ bằng bao nhiêu? 

Cho hình chóp SABC có $SB=SC=BC=CA=a.$. Hai mặt (ABC) và (ASC) cùng vuông góc với (SBC). Tính thể tích hình chóp.

Cho phương trình:

$(m -1){\log }_{\frac{1}{2}}^2{\left(x-2\right)}^2+4\left(m-5\right){\log }_{\frac{1}{2}}\frac{1}{x-2}+4m-4=0$ (với m là tham số). Gọi $S= [a;b]$ là tập các giá trị của m để phương trình có nghiệm trên đoạn $\left[\frac{5}{2};4\right]$. Tính a+b.

Cho hàm số $\left(C_m\right):y= x^3+ m{x}^2- 9x- 9m.$Tìm m $\left(C_m\right)$để tiếp xúc với Ox:

Cho hàm số $\left(C_m\right):y= x^3+ m{x}^2- 9x- 9m.$Tìm m $\left(C_m\right)$để tiếp xúc với Ox:

Cho hàm số $y=x^3-3x^2+5x-2$ có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) có hệ số góc nhỏ nhất. 

Tìm tổng các nghiệm của phương trình sau:

${\log }_{\sqrt[4]{5}}\left(x^2-2x-3\right)=2{\log }_2\left(x^2-2x-4\right)$

Cho hàm số y = f(x) xác định và có đạo hàm y=f'(x). Đồ thị của hàm số y = f'(x) như hình dưới đây.

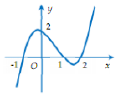
Khẳng định nào sau đây là đúng?

Cho hàm số $y=\frac{3x}{1+2x}$ . Khẳng định nào sau đây là khẳng định đúng ?

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng $a\sqrt{2}$. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.

Cho hàm số $y=x^3-3x^2+5x-2$ có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) có hệ số góc nhỏ nhất. 

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng $a\sqrt{2}$. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.