Câu hỏi:
10/11/2024 286Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3;4;5;6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
A. 781
B. 624
C. 816
D. 342
Trả lời:
Giải bởi Vietjack
Đáp án đúng là A
Lời giải:
Tổng số điểm vừa lấy bằng: 3 + 4 + 5 + 6 = 18 (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: = 816(cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: 
(cách chọn).
Vậy số tam giác cần tìm bằng: 816 - 35 = 781(tam giác).
*Phương pháp giải:
Tính số tam giác lập được từ các trường hợp
+Hai đỉnh cùng thuộc 1 đường thẳng đỉnh thứ 3 thuộc đường thẳng còn lại
+ Mỗi đỉnh thuộc một đường thẳng.
*Lý thuyết:
Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các tổ hợp chập k của một tập hợp có n phần tử là : .
- Tính chất :
- Đặc điểm: Tổ hợp là chọn phần tử không quan trọng thứ tự, số phần tử được chọn là k: 0 ≤ k ≤ n
Xem thêm
Công thức tính tổ hợp chập k của n và cách giải các dạng bài tập
TOP 40 câu Trắc nghiệm Hoán Vị - Chỉnh Hợp – Tổ Hợp (có đáp án ) – Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng hai cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
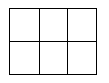
Câu 3:
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247
Câu 6:
Có bao nhiêu cách chia hết 4 chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất 1 chiếc.
Câu 7:
Cho tam giác ABC, gọi S là tập hợp gồm 4 đường thẳng song song với AB, 6 đường thẳng song song với BC và 8 đường thẳng song song với AC. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng thuộc tập 
Câu 8:
Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau, sao cho trong mỗi số đó nhất thiết phải có mặt chữ số 0?
Câu 9:
Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh, 1 nam và 1 nữ để phân công trực nhật. Số cách chọn là
Câu 10:
Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh là đỉnh của đa giác đều đã cho?
Câu 11:
Một tập hợp M có tập con. Hỏi M có bao nhiêu tập con có ít nhất 2017 phần tử?
Câu 12:
Có bao nhiêu cách bỏ đồng thời 7 quả bóng bàn giống nhau vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả?
Câu 13:
Cho k, n(k < n) là các số nguyên dương, mệnh đề nào dưới đây sai?
Câu 14:
Gieo 2 xúc xắc màu xanh và đỏ cùng 1 lần. Hỏi có bao nhiêu khả năng xảy ra số chấm xuất hiện của xúc xắc màu xanh nhiều hơn số chấm xuất hiện trên xúc xắc màu đỏ.
Câu 15:
Số tập con gồm nhiều nhất 3 phần tử của tập A = {1,2,....,10} là
