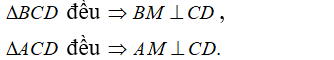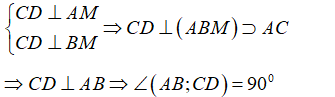Câu hỏi:
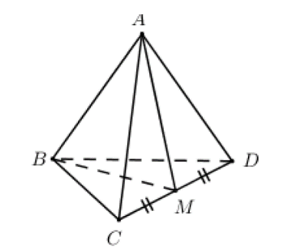
05/12/2024 223Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B.
*Lời giải
- Phương pháp: Tứ diện đều có các cặp cạnh đối vuông góc.
- Cách giải:
+ Gọi M là trung điểm của CD ta có:
+ Ta có:
*Phương pháp giải
Tứ diện đều có cặp cạnh đối vuông góc với nhau
*Lý thuyến cần nắm về góc giữa hai mặt phẳng:
1. Góc giữa 2 mặt phẳng là gì?
- Khái niệm: Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
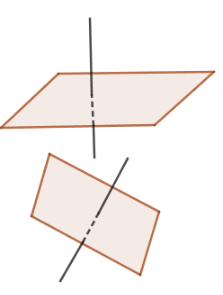
Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘góc khối’, là phần không gian bị giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.
2. Tính chất của góc giữa 2 mặt phẳng
Từ định nghĩa trên ta có:
- Góc giữa 2 mặt phẳng song song bằng 0 độ,
- Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.
3. Cách xác định góc giữa 2 mặt phẳng
Gọi P là mặt phẳng 1, Q là mặt phẳng 2
Trường hợp 1: Hai mặt phẳng (P), (Q) song song hoặc trùng nhau thì góc của 2 mặt phẳng bằng 0,
Trường hợp 2: Hai mặt phẳng (P), (Q) không song song hoặc trùng nhau.
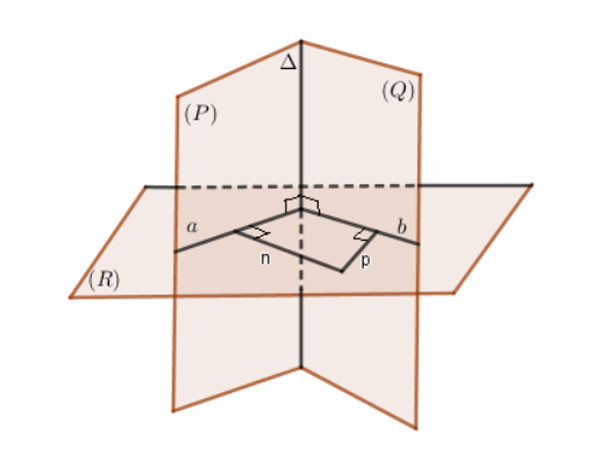
Công thức và phương pháp tính góc giữa hai mặt phẳng
1. Công thức tính góc giữa hai mặt phẳng
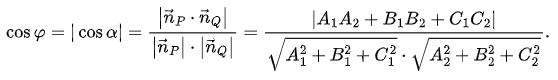
2. Cách tính góc giữa 2 mặt phẳng
a. Sử dụng hệ thức lượng trong tam giác vuông, định lý hàm số sin, hàm số cos.
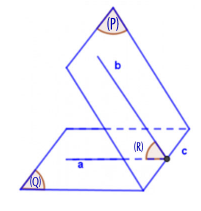
b. Dựng mặt phẳng phụ (R) vuông góc với giao tuyến c mà (Q) giao với (R) = a, (P) giao với (R) = b.
Suy ra ![]()
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết, cách xác định và bài tập tính góc giữa 2 mặt phẳng
Góc giữa hai mặt phẳng (lý thuyết, công thức) các dạng bài tập và cách giải
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Viết phương trình tiếp tuyến kẻ từ điểm A (2; 3) tới đồ thị hàm số là
Câu 2:
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ điểm D đến đường thẳng BC là a. Gọi H là trung điểm BC, I là trung điểm AH.
1) Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (ADH) và DH = a.
2) Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).
3) Tính khoảng cách giữa AD và BC.
Câu 3:
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD). Biết . Tính góc giữa SC và mp (ABCD).
Câu 4:
Cho hình chóp S.ABC có SA = SB = SC và . Hãy xác định góc giữa cặp vectơ và ?
Câu 5:
Phần I: Trắc nghiệm
Cho hàm số . Đạo hàm y’ của hàm số là biểu thức nào sau đây?
Câu 7:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:
Câu 8:
Cho hàm số , có đồ thị là (C). Tìm biết tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox có phương trình là ?
Câu 10:
Cho chuyển động thẳng xác định bởi phương trình (t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?
Câu 14:
Cho hàm số có đồ thị (C).
a) Giải bất phương trình: f'(x) ≤ 0.
b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 1.