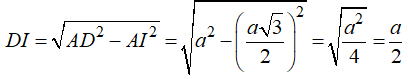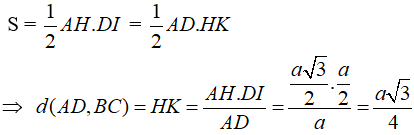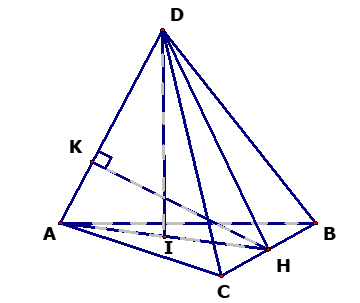
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ điểm D đến đường thẳng BC là a. Gọi H là trung điểm BC, I là trung điểm AH.

1) Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (ADH) và DH = a.

2) Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).

3) Tính khoảng cách giữa AD và BC.

Viết phương trình tiếp tuyến kẻ từ điểm A (2; 3) tới đồ thị hàm số $y=\frac{3x+4}{x-1}$ là

Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD). Biết $SA=\frac{a\sqrt{6}}{3}$ . Tính góc giữa SC và mp (ABCD).

Cho hình chóp S.ABC có SA = SB = SC và $\widehat{ASB} = \widehat{BSC} = \widehat{CSA}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow{SB}$ và $\overrightarrow{AC}$?

Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:

Phần I: Trắc nghiệm

Cho hàm số $y=\frac{-x^2+2x-3}{x-2}$. Đạo hàm y’ của hàm số là biểu thức nào sau đây?

Tìm các giới hạn sau: $\underset{x\to 1}{\lim }\frac{x-\sqrt{2x-1}}{x^2-12x+11}$

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:

Cho hàm số $y = \frac{ax+b}{x-2}$, có đồ thị là (C). Tìm biết tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox có phương trình là $y=-\frac{1}{2}x+2$?

Tìm a,b để hàm số $f\left(x\right)=\left\{\begin{array}{l}{x}^2+1 khi x\ge 0\\ 2x^2+ax+b khi x<0\end{array}\right.$ có đạo hàm tại x = 0?

Cho chuyển động thẳng xác định bởi phương trình $s=t^3-3t^2-9t+2$ (t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?

Cho hình lập phương ABCD.A’B’C’D’. Hệ thức nào sau đây đúng?

Phần II: Tự luận

Tìm các giới hạn sau: $\underset{x\to 1}{\lim }\frac{3x^2-2x-1}{x^3-1}$

Cho dãy số $\left(u_n\right)$ xác định bởi $u_n=\frac{2^n\sin n}{9^n}$. Tính $lim u_n$

Cho hàm số $y=f\left(x\right)=-x^3-3x^2 +9x+2011$ có đồ thị (C).

a) Giải bất phương trình: f'(x) ≤ 0.

b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 1.

Đạo hàm của hàm số $f\left(x\right)={\left(\frac{2x+1}{x+1}\right)}^{2018}$ là: