Câu hỏi:
12/10/2024 7,002Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N theo thứ tự là trung điểm AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH
A. HB = 12cm; HC = 28cm; AH = 20cm
B. HB = 15cm; HC = 30cm; AH = 20cm
C. HB = 16cm; HC = 30cm; AH = 22cm
D. HB = 18cm; HC = 32cm; AH = 24cm
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Phương pháp giải
- do M, N là trung điểm 2 cạnh AB, AC nên sử dụng tính chất đường trung tuyến trên 2 cạnh và vào 2 tam giác vuông con: AHB vuông tại H và AHC vuông tại H
- Áp dụng định lý pythago vào tam giác vuông ABC để tính ra BC
- Áp dụng hệ thức lượng về đường cao AH để tính ra BH và CH rồi tính ra AH
*Lời giải
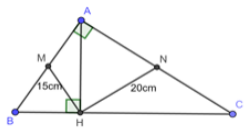
Xét ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABC vuông tại A có:
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
* Công thức về hệ thức lượng giữa cạnh và đường cao trong tam giác vuông:
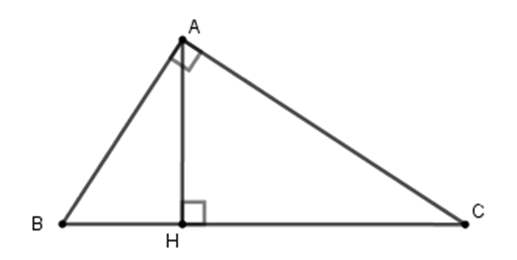
Cho ∆ABC vuông tại A có : AH là đường cao. (Như hình vẽ dưới)
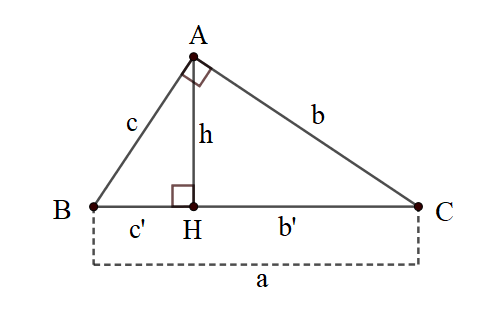
Ta có: AB = c ; AC = b ; BC = a
AH = h (đường cao); BH = c’ (hình chiếu của c); CH = b’ (hình chiếu của b)
Khi đó, ta có các hệ thức như sau :
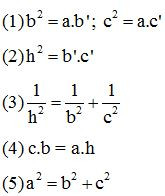
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông
Bài tập về Hệ thức giữa cạnh và đường cao trong tam giác vuông
Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH = 6cm. Tính độ dài các đoạn thẳng CH
Câu 2:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
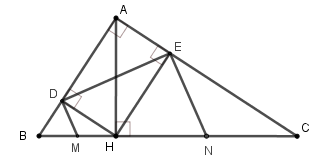
Tính độ dài đoạn thẳng DE
Câu 3:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm. Tính độ dài các cạnh AC, BC của tam giác ABC.
Câu 4:
Cho tam giác ABC vuông tại A, AH BC (H thuộc BC). Cho biết AB : AC = 3 : 4 và BC = 15cm. Tính độ dài đoạn thẳng BH
Câu 5:
Cho ABC vuông tại A, các cạnh AB, AC tương ứng tỉ lệ với 3 và 4. Biết đường cao AH = 18.
Tính chu vi ABC
Câu 6:
Cho tam giác ABC vuông tại A có cạnh AB = 30cm và AC = 40cm, đường cao AH, trung tuyến AM. Tính BH, HM, MC
Câu 7:
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
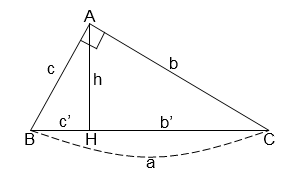
Câu 8:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
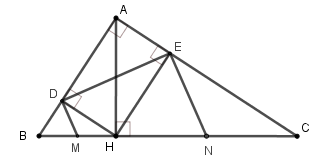
Tính độ dài đoạn thẳng DE.
Câu 9:
Cho ABC cân tại A, kẻ đường cao AH và CK. Biết AH = 7,5cm; CK = 12cm. Tính BC, AB
Câu 10:
Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN
Câu 11:
Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?

Câu 13:
Cho tam giác ABC vuông tại A, AH BC (H thuộc BC). Cho biết AB : AC = 4 : 5 và BC = cm. Tính độ dài đoạn thẳng CH (làm tròn đến chữ số thập phân thứ nhất.
Câu 14:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 5 : 12 và AB + AC = 34. Tính các cạnh của tam giác ABC
Câu 15:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 4cm, . Tính chu vi tam giác ABC