Câu hỏi:
18/07/2024 164Cho một miếng tôn mỏng hình chữ nhật ABCD, với AB = 4dm và AD = 9dm. Trên cạnh AD lấy điểm E sao cho AE = 3dm trên cạnh BC lấy điểm F là trung điểm của BC (tham khảo hình 1 ). Cuộn miếng tôn lại một vòng sao cho cạnh AB và DC trùng khít nhau. Khi đó miếng tôn tạo thành mặt xung quanh của một hình trụ (tham khảo hình 2).
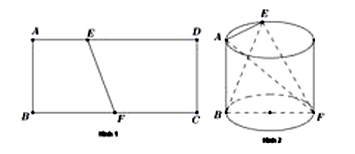
Thể tích V của tứ diện ABEF trong hình 2 bằng
A. 3√32π2dm2.
B. 27√32π2dm2.
C. 9√32π2dm2.
D. 81√32π2dm2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
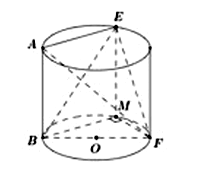
Khi cuộn miếng tôn (hình 1) thành mặt xung quanh của hình trụ (hình 2) thì chiều cao của hình trụ bằng h = 4dm và chu vi đáy của hình trụ là 9dm
Gọi r là bán kính đáy của hình trụ ⇒2πr=9⇒r=92πdm.
Độ dài đường kính BF=2r=9πdm.
Kẻ EM//AB(M∈→BF), vì AE=13AD⇒→AE=→BM=23→BF⇒^BFM=600 và ^MBF=300
Tam giác BMF vuông tại M⇒BM=BF.sin^BFM=9√32πdm⇒AE=9√32πdm.
Ta có BM//AE⇒^(AE,BF)=^MBF=300
⇒VABEF=16AE.BF.d(AE,BF).sin^(AE,BF)=16.AE.BF.AB.sin^MBF
⇒VABEF=27√32π2dm3.
Chọn B.

Khi cuộn miếng tôn (hình 1) thành mặt xung quanh của hình trụ (hình 2) thì chiều cao của hình trụ bằng h = 4dm và chu vi đáy của hình trụ là 9dm
Gọi r là bán kính đáy của hình trụ ⇒2πr=9⇒r=92πdm.
Độ dài đường kính BF=2r=9πdm.
Kẻ EM//AB(M∈→BF), vì AE=13AD⇒→AE=→BM=23→BF⇒^BFM=600 và ^MBF=300
Tam giác BMF vuông tại M⇒BM=BF.sin^BFM=9√32πdm⇒AE=9√32πdm.
Ta có BM//AE⇒^(AE,BF)=^MBF=300
⇒VABEF=16AE.BF.d(AE,BF).sin^(AE,BF)=16.AE.BF.AB.sin^MBF
⇒VABEF=27√32π2dm3.
Chọn B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x)=ax−2bx+c với a,b,c∈ℝ có bảng biến thiên như hình vẽ bên.
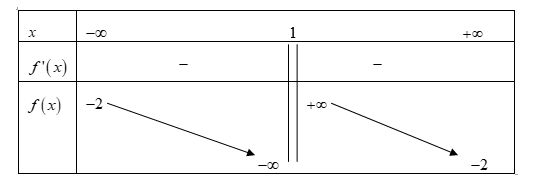
Giá trị a + c thuộc khoảng nào dưới đây?
Cho hàm số f(x)=ax−2bx+c với a,b,c∈ℝ có bảng biến thiên như hình vẽ bên.

Giá trị a + c thuộc khoảng nào dưới đây?
Câu 2:
Cho hàm số f(x) = sinx - 1. Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số f(x) = sinx - 1. Trong các khẳng định sau, khẳng định nào đúng?
Câu 5:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ dưới đây?
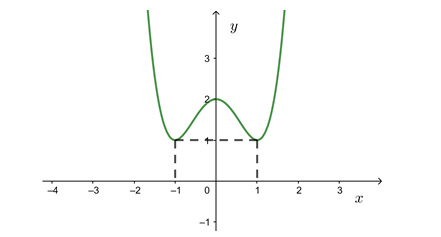

Câu 6:
Gọi z1,z2 lần lượt là hai số phức thỏa mãn |z1+4+2i|=√13 và |z2+8−2i|=|z2−4−10i|. Giá trị nhỏ nhất của biểu thức |z1−z2|+|z2+5−4i| thuộc khoảng nào dưới đây?
Gọi z1,z2 lần lượt là hai số phức thỏa mãn |z1+4+2i|=√13 và |z2+8−2i|=|z2−4−10i|. Giá trị nhỏ nhất của biểu thức |z1−z2|+|z2+5−4i| thuộc khoảng nào dưới đây?
Câu 7:
Trong không gian Oxyz, cho hai điểm P(5; -2; 3), Q(3; -3; 1). Mặt cầu tâm Q và đi qua điểm P có phương trình là
Trong không gian Oxyz, cho hai điểm P(5; -2; 3), Q(3; -3; 1). Mặt cầu tâm Q và đi qua điểm P có phương trình là
Câu 8:
Thể tích khối chóp có chiều cao h = 4 và diện tích đáy B = 9 bằng
Thể tích khối chóp có chiều cao h = 4 và diện tích đáy B = 9 bằng
Câu 9:
Trong không gian Oxyz, đường thẳng d:{x=2+ty=1+tz=−2+t đi qua điểm nào trong các điểm dưới đây?
Trong không gian Oxyz, đường thẳng d:{x=2+ty=1+tz=−2+t đi qua điểm nào trong các điểm dưới đây?
Câu 10:
Nếu 1∫0f(x)dx=2 và 1∫0g(x)dx=3 thì 1∫0[2020f(x)−2021g(x)]dx bằng
Nếu 1∫0f(x)dx=2 và 1∫0g(x)dx=3 thì 1∫0[2020f(x)−2021g(x)]dx bằng
Câu 11:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a. Gọi M là trung điểm của BC biết góc giữa đường thẳng A'M và mặt phẳng (ABC) bằng 600 (tham khảo hình bên). Khoảng cách từ điểm A' đến mặt phẳng (ABC) bằng
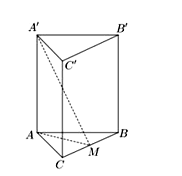
Câu 12:
Cho hàm số y = f(x) có bảng biến thiên như hình bên.
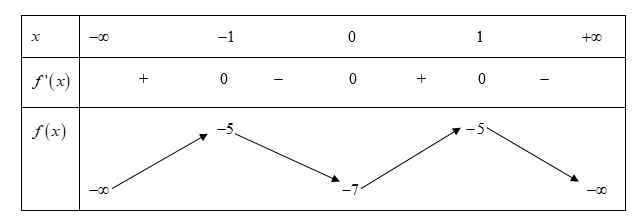
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
Cho hàm số y = f(x) có bảng biến thiên như hình bên.

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
Câu 13:
Cho F(x) là một nguyên hàm của hàm số f(x) = 4x + cos2x thỏa mãn F(0) = 1. Giá trị F(π) bằng
Cho F(x) là một nguyên hàm của hàm số f(x) = 4x + cos2x thỏa mãn F(0) = 1. Giá trị F(π) bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)